六年级上册数学课件-7 鸽巢问题丨苏教版 (2)

六年级上册数学课件-7 鸽巢问题丨苏教版 (2)

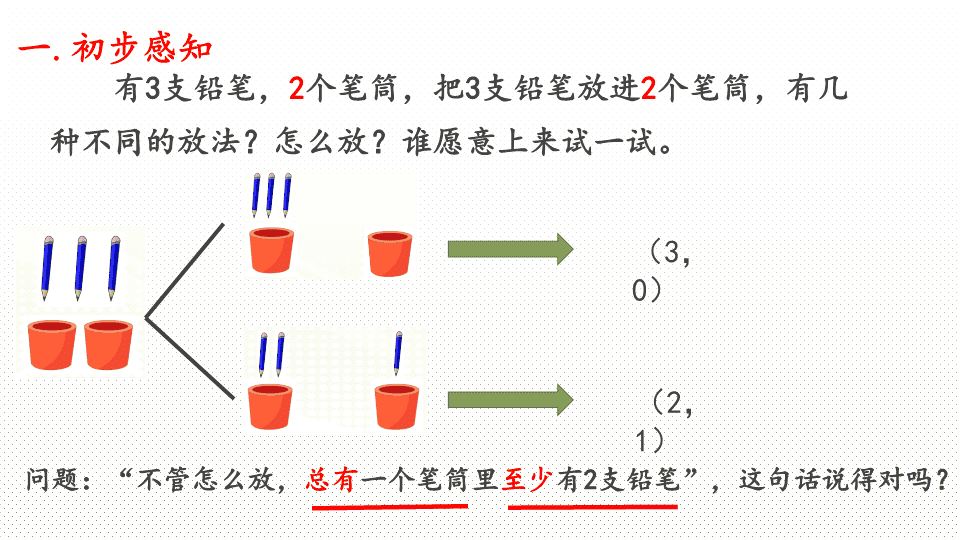
鸽巢问题 抽屉原理 现在老师任意点13位同学，我就可以肯定，至少有2个同学的生日在同一个月。你们信吗？ ？ 也就是2人或2人以上，反过来，生日在同一个月的可能有2人，可能3人、4人、5人……，也可以用一句话概括就是“至少有2人” 一 . 初步感知 有3支铅笔， 2 个笔筒，把3支铅笔放进 2 个笔筒， 有几种不同的放法 ？ 怎么放 ？谁愿意上来试一试。 （2，1） （3，0） 问题：“不管怎么放， 总有 一个笔筒里 至少 有2支铅笔”，这句话说得对吗？ 初步感知小总结 从 刚才把3支铅笔放进2个笔筒的实验中，我们可以得到什么？ 得到结论： 我们可以得到3支铅笔放进2个笔筒， 总有 一个笔筒 至少 放进2支笔。 二 . 列举法 小组合作： （1）画一画：借助“画图”或“数的分解”的方法把各种情况都表示出来； （2）找一找：每种摆法中最多的一个笔筒放了几支，用笔标出； （3）可以发现：总有一个笔筒至少放进了（  ）支铅笔。 如果现在有4支铅笔放进3个笔筒，还会出现这样的结论吗？ 四种情况：（4，0，0）、（3，1，0）、（2，1，1）、（2，2，0） 2 每种摆法中最多的一个笔筒放进了：4支、3支、2支。 列举法率小总结 疑问： 我们能不能找到一种更为直接的方法，只摆一种情况，也能得到这个结论，找到 “至少数” 呢？ 4支铅笔放进3个笔筒，通过列举可以得到 四种情况： （4，0，0） （3，1，0） （2，1，1） （2，2，0） 得到结论： 总有一个笔筒至少放进了 2 支铅笔。 还可以这样想：先放 3 支，在每个笔筒中放 1 支，剩下的 1 支就要放进其中的一个笔筒。所以至少有一个笔筒中有 2 支铅笔。 三 . 假设法 （1）这种分法的实质就是先怎么分的？ （2）为什么要一开始就平均分？ 平均分可以使每个笔筒的笔尽可能 少一点，方便找到“至少数”。 （3）怎样用算式表示这种方法？ 算式中的两个“1”是什么意思？ 4÷3= 1 支…… 1 支  1 + 1 ＝2支 放进哪个笔筒都行 平均分 余下的1支，怎么放？ 三 . 假设法 —— 引伸拓展 列出算式，依据算式说理。 （1）5支笔放进4个笔筒，总有一个笔筒至少放进（   ）支笔。 （2）26支笔放进25个笔筒，总有一个笔筒至少放进（  ）支笔。 （3）100支笔放进99个笔筒，总有一个笔筒至少放进（  ）支笔。 2 2 2 5 ÷ 4 = 1 支…… 1 支  1 + 1 ＝2支 26 ÷ 25 = 1 支…… 1 支  1 + 1 ＝2支 26 ÷ 25 = 1 支…… 1 支  1 + 1 ＝2支 得到结论： 刚才的这种方法就是“假设法”，它里面就蕴含了“平均分”，我们用有余数的除法算式把平均分的过程简明的表示出来了，也就是求“ 至少数 ”时，我们可以用 平均分！ 假设法小总结 四 . 建立模型 把 5 支笔放进 3 支笔筒，用假设法解决会有什么结论？ 5÷3=1 支 ……2 支 总有一个笔筒里至少有 2 支。 总有一个笔筒里至少有 3 支。 2. 为什么第二次平均分？ 保证 “ 至少 ” 平均分 1. 先平均分的是什么？余下的 2 支怎么办？ 小组讨论 （ 3 ） 23 支笔放进 4 个笔筒，至少几支放进同一个笔筒？ 四 . 建立模型 —— 强化练习 对比算式，发现什么规律？ 如果把笔和笔筒的数量进一步增加呢？ （ 1 ） 10 支笔放进 7 个笔筒，至少几支放进同一个笔筒？ 10÷7 ＝ 1 （支） …3 （支） 1 + 1 ＝ 2 （支） （ 2 ） 14 支笔放进 4 个笔筒，至少几支放进同一个笔筒？ 14÷4 ＝ 3 （支） …2 （支） 3 + 1 ＝ 4 （支） 23÷4 ＝ 5 （支） …3 （支） 5 + 1 ＝ 6 （支） 先平均分，再用所得的 “ 商 +1” 与余数无关，不管余多少，都要再平均分 和余数有没有关系？ 刚才我们研究了笔放入笔筒的问题，那如果换成鸽子飞进鸽笼你会解答吗？把苹果放入抽屉，把书放入书架，高速路口同时有 4 辆车通过 3 个收费口 …… ，类似的问题我们都可以用这种方法解答。 四 . 建立模型 —— 引申拓展 鸽巢原理 鸽巢原理的由来 同学们这节课从数学的角度分析了这些事情，同时根据数据特征，发现了这些规律。你们发现的这个规律和一位数学家发现的规律一模一样，只不过他是在 150 多年前发现的，你们知道他是谁吗？ —— 德国数学家？ “ 狄里克雷 ” ，后人们为了纪念他从这么平凡的事情中发现的规律，就把这个规律用他的名字命名，叫 “ 狄里克雷原理 ” ，由于人们对鸽子飞回鸽巢这个引起思考的故事记忆犹新，所以人们又把这个原理叫做 “ 鸽巢原理 ” ，它还有另外一个名字叫 “ 抽屉原理 ” 。 五、解决问题 1 、老师上课时提出的生日问题，现在你能解释吗？ 2 、 11 只鸽子飞进了 4 个鸽笼，总有一个鸽笼至少飞进了 3 只鸽子。为什么？ 3 、 5 个人坐 4 把椅子，总有一把椅子上至少坐 2 人。为什么？ 4 、 15 本书放进 4 个抽屉，不管怎么放，总有一个抽屉至少有 4 本书，为什么？ 收获了什么？