六年级下册数学试题-小升初数学思维训练综合练习十（含答案）全国通用

六年级下册数学试题-小升初数学思维训练综合练习十（含答案）全国通用

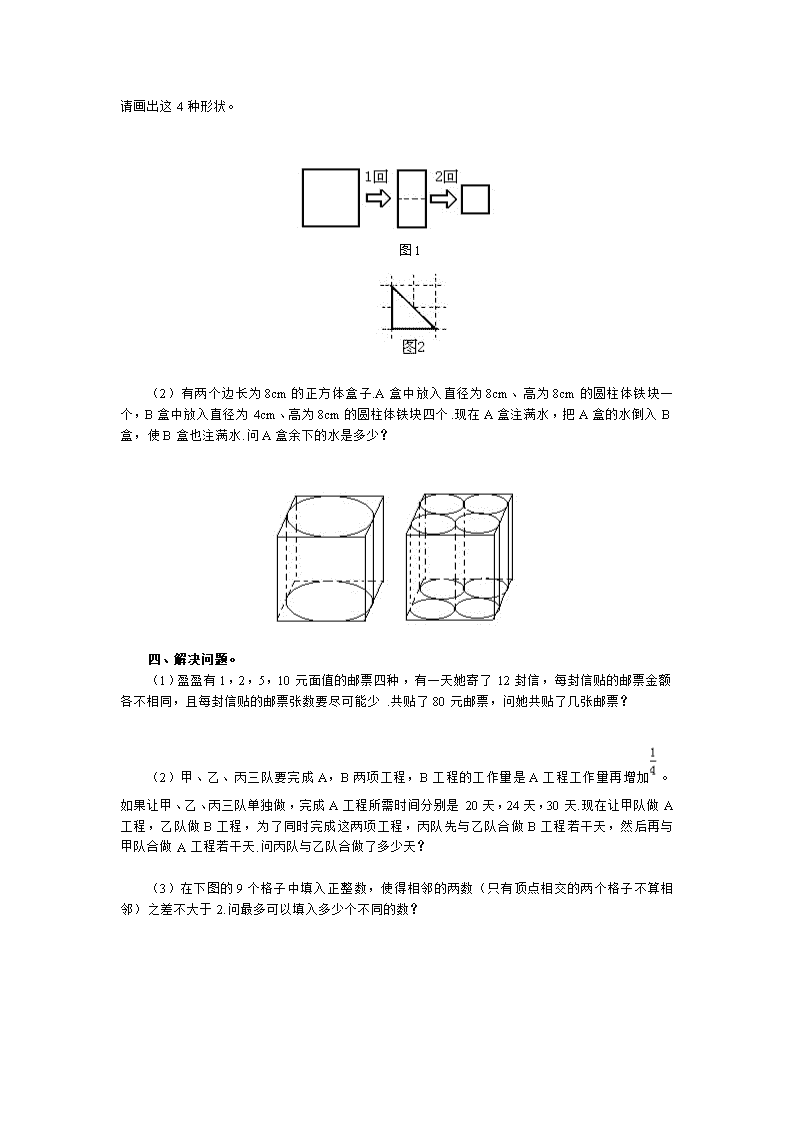
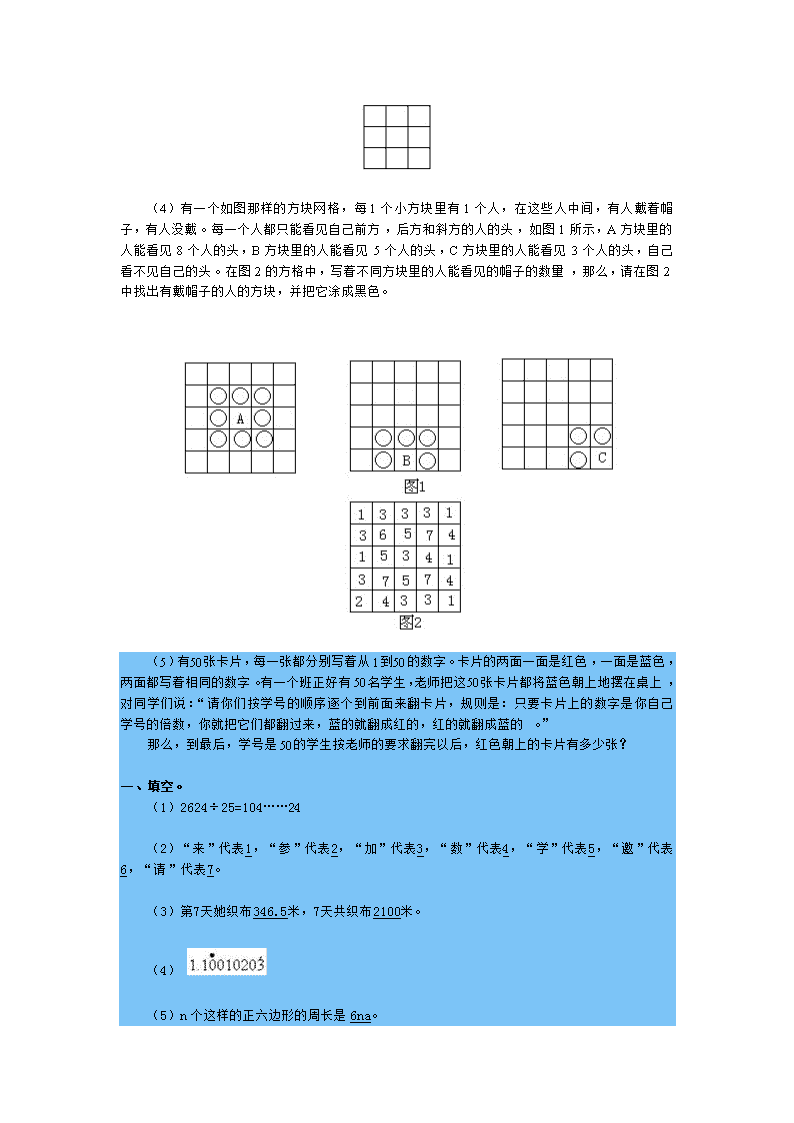
小升初数学思维训练综合练习十 一、 填空。 　　（1）下面算式中的两个方框内应填什么数，才能使这道整数除法题的余数为最大。 　　□÷25=104……□ 　　（2）右边乘法算式中的“来参加数学邀请赛”八个字，各代表一个不同的数字。其中“赛”代表9，“来”代表____，“参”代表____，“加”代表____，“数”代表______，“学”代表____，“邀”代表____，“请”代表____。 ‎ ‎　　（3）王阿姨用新机器织布。第一天织布253.5米，以后提高了织布技术，每天都比前一天多织布15.5米。第7天她织布（　　 ）米，7天共织布（　　 ）米。 　　 尽可能小，这个新的循环小数是（　　 ）。 　　（5）下图是由边长a的6个等边三角形拼成的正六边形。n个这样的正六边形的周长是 （　　 ）。 ‎ ‎　　二、计算。 　　 　　（2）1.1+1.3+1.5+…+9.9 　　（3）99＋198＋297+396+495＋594+693＋792＋891+990 　　 　　三、操作题。 ‎ ‎　　（1）将一正方形的纸对折2次后，还是正方形（见图1）。用同样的方法，可把某形状的纸对折3次后，成为图2那样的三角形。已知可把4种形状的纸对折3次后，折成那样的三角形，请画出这4种形状。 　　 ‎ ‎ 　　图1 　　 ‎ ‎　　（2）有两个边长为8cm的正方体盒子.A盒中放入直径为8cm、高为8cm的圆柱体铁块一个，B盒中放入直径为4cm、高为8cm的圆柱体铁块四个.现在A盒注满水，把A盒的水倒入B盒，使B盒也注满水.问A盒余下的水是多少？ 　　 ‎ ‎　　四、解决问题。 　　（1）盈盈有1，2，5，10元面值的邮票四种，有一天她寄了12封信，每封信贴的邮票金额各不相同，且每封信贴的邮票张数要尽可能少.共贴了80元邮票，问她共贴了几张邮票？ 　　（2）甲、乙、丙三队要完成A，B两项工程，B工程的工作量是A工程工作量再增加。如果让甲、乙、丙三队单独做，完成A工程所需时间分别是20天，24天，30天.现在让甲队做A工程，乙队做B工程，为了同时完成这两项工程，丙队先与乙队合做B工程若干天，然后再与甲队合做A工程若干天.问丙队与乙队合做了多少天？ 　　（3）在下图的9个格子中填入正整数，使得相邻的两数（只有顶点相交的两个格子不算相邻）之差不大于2.问最多可以填入多少个不同的数？ 　　 ‎ ‎　　（4）有一个如图那样的方块网格，每1个小方块里有1个人，在这些人中间，有人戴着帽子，有人没戴。每一个人都只能看见自己前方，后方和斜方的人的头，如图1所示，A方块里的人能看见8个人的头，B方块里的人能看见5个人的头，C方块里的人能看见3个人的头，自己看不见自己的头。在图2的方格中，写着不同方块里的人能看见的帽子的数量，那么，请在图2中找出有戴帽子的人的方块，并把它涂成黑色。 　　 ‎ ‎　　（5）有50张卡片，每一张都分别写着从1到50的数字。卡片的两面一面是红色，一面是蓝色，两面都写着相同的数字。有一个班正好有50名学生，老师把这50张卡片都将蓝色朝上地摆在桌上，对同学们说：“请你们按学号的顺序逐个到前面来翻卡片，规则是：只要卡片上的数字是你自己学号的倍数，你就把它们都翻过来，蓝的就翻成红的，红的就翻成蓝的。” 　　那么，到最后，学号是50的学生按老师的要求翻完以后，红色朝上的卡片有多少张？ 一、填空。 　　（1）2624÷25=104……24 　　（2）“来”代表1，“参”代表2，“加”代表3，“数”代表4，“学”代表5，“邀”代表6，“请”代表7。 　　（3）第7天她织布346.5米，7天共织布2100米。 　　（4） 　　（5）n个这样的正六边形的周长是6na。 ‎ ‎ 　　二、计算。 　　 　　（2）1.1+1.3+1.5+…+9.9 　　=（1.1+9.9）÷2×45 　　=5.5×45 　　=247.5 　　（3）99＋198＋297+396+495＋594+693＋792＋891+990 　　=100-1+200-2+300-3＋…＋1000-10 　　=100＋200＋300＋…+1000-（1＋2＋3+…＋10） 　　=5500-55 　　=5445 　　（4）原式 　　 　　三、操作题。 　　（1）‎ ‎　　（2）余下的水量是0. 　　直径为8的圆面积，是直径为4的圆面积的4倍.高一样，1个大圆柱体积，与4个小圆柱体积相等，A盒与B盒空隙的容积相等. 　　四、解决问题。 　　（1）共贴了23张邮票. 　　1， 2， 5， 10各 1张： 3=1+2，4＝ 2 ＋ 2，6＝ 1＋ 5，7＝2＋5， 11＝ 1＋10各 2张；8= 1＋2＋5，9=2＋2＋5， 14＝ 2＋2 +10各3张.（也可以 12＝2＋10，13＝ 1＋ 2＋ 10来代替和 14）因为1＋ 2＋…＋12=78.80比 78多 2，所以只能是 12＋ 2=14，或者 11＋1＝12，12 +1＝13 　　（2）丙队与乙队合做15天. 　　设A工程的工作量为 120（ 20， 24， 30的最小公倍数）， B工程 　　把两项工程都完成，三队都需做（120＋150）÷（6＋5＋4）＝18（天）. 　　丙队要帮乙队做（150-5×18）÷4=15（天）. 　　（3）最多可填入不同的7个数. 　　考虑图（a）那样的四个方格.很明显，斜角两数相差最多是4.如果相差4，C，D两数与A、与B都相差2.C和D是同一数.只有相差3，这四个数才能都不相同.对九个方格来说，如果左上角一格填1，右下角一格最多填9.不论填9，或填8，填7，根据上面分析，最多只能填7个不同的数.具体例子见图（b）.‎ ‎　　（4） 　　①站在第一行第五列的人能看见1顶帽子，说明他周围的3人有2人没戴帽子。 　　②站在第二行第四列的人能看见7顶帽子，说明他周围的8人中只有1人没戴帽子，综合结论①可知他本人没有戴帽子。 　　③站在第二行第五列的人能看到4顶帽子，且他周围的5人中已有1人没戴帽子，说明其余4人均戴帽子，根据结论①可知他本人没戴帽子。 　　④利用上下对称原理可以分析出：站在第四行、第五行后三列的6个人中，只有第四行第四列、第五列两人没戴帽子，其他人均戴帽子。 　　⑤站在第四行第二列的人能看到7顶帽子，说明他周围的8人中只有1人没戴帽子。 　　⑥站在第三行第1列的人能看见1顶帽子，说明他周围的5人中只有1人戴帽子。综合结论⑤‎ 可知：这1人不可能是第二行第一二列的人，也不可能是第四行第二列的人。所以只能是站在第三行第二列的人或第四行第一列的人。 　　⑦站在第五行第一列的人能看到2顶帽子，说明结论⑥所说戴帽子的人站在第四行第一列。 　　⑧站在第二行第二列的人能看到6顶帽子，说明站在第一行第一、二列的2人都戴帽子。 　　综合上述分析，可以看到“思考的顺序”是解答本题的关键。 　　答案如下图所示。‎ ‎　　（5）解 每张卡片，所写数字有几个约数就被翻过几次。被翻了奇数次的卡片红色面朝上，而只有完全平方数才能有奇数个约数，所以本题也就是求写有完全平方数的卡片有几张，所以红色朝上的卡片共有7张。 ‎