六年级数学教案 《简单的组合》

六年级数学教案 《简单的组合》

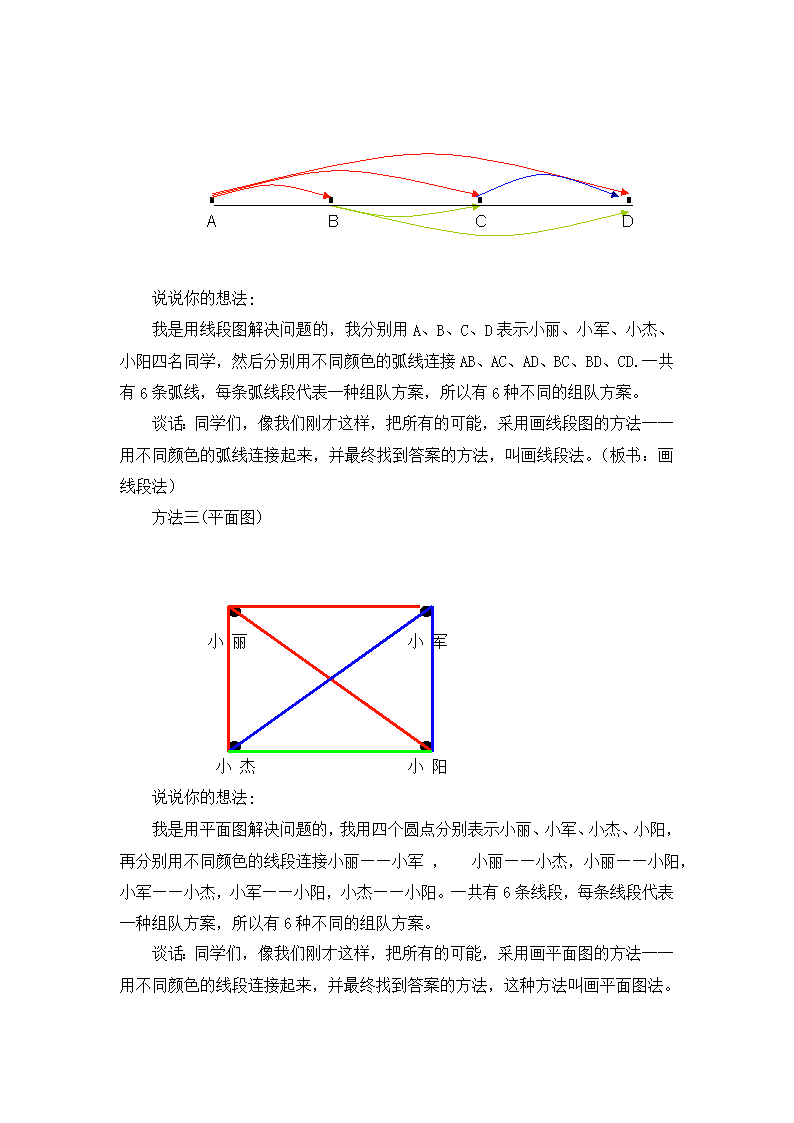
简单的组合 教学内容： 六年级数学下册数学与生活简单的组合的内容。‎ 教学目标:‎ ‎1.利用已有经验认识和了解简单的“组合”，掌握解决问题的策略和方法，体会解决问题策略的多样性。‎ ‎2.培养初步的观察、分析及推理能力，能有序地、全面地思考问题。‎ ‎3.尝试用数学的方法来解决生活中的实际问题，感受数学在现实生活中的广泛应用。‎ ‎4.在数学活动中养成与他人合作的良好习惯，并初步学会表达解决问题的大致过程和结果。‎ 教学重难点：‎ 教学重点：训练学生思维的有序性，学会解决这类问题的策略和方法。‎ 教学难点：通过数形结合，掌握解决问题的方法。‎ 教具学具： 相关表格 课件 教学过程：‎ 一、创设情境，提出问题 ‎1.谈话：告诉大家一个好消息，六一儿童节期间学校要组织“少儿戏曲大赛”,规定每班只须2人组队参赛，我们班小丽、小军、小杰、小阳四名同学都想参加，要想从他们当中选出2名参加，有多少种不同的组队方案？ ‎ 出示课本情境图：‎ 谈话：请同学们想一想，我们有多少种组队方案可以选择呢？(板书:组合)‎ 二、自主学习，小组探究。‎ ‎1、谈话：你想用什么方法解决这个问题？在小组内交流一下。‎ 自主学习提示：‎ ‎（1）想一想，有多少种组队方案？要求没有重复、没有遗漏。‎ ‎（2）在小组内合作，重点说说自己方案的做法。并试着用简单的图形表示出不同的组队方案。‎ ‎（3）尝试用不同的方法解决这个问题。‎ 教师参与到学生的探究中，学生按自己的方案解决问题。‎ 三、汇报交流，评价质疑 ‎1.同学们都按照自己小组的方案解决了问题。现在哪个小组愿意向同学们汇报？‎ 教师根据学生的介绍，将学生所说的过程在实物投影仪商展示出来。‎ 预设：‎ 方案1（枚举法）：‎ 学生1：我这样想的： ‎ ‎ 小军 小杰 小丽 小杰 小军 小杰 小阳 ‎ 小阳 小阳 ‎ 说说你的想法:‎ ‎ 我是先固定小丽同学，再分别与小军、小杰、小阳组合，有三种组合；然后再固定小军同学，再分别与小杰、小阳组合，有两种组合；最后固定小杰同学，再与小阳组合，有一种组合 。我们班可以派小丽和小军、小丽和小杰、小丽和小阳、小军和小杰、小军和小阳、小杰和小阳，一共有6种组合，所以有6种不同的组队方案。‎ 谈话：像我们刚才那样，把所有的可能，采用列举的方法一一写下来，并最终找到答案的方法，叫枚举法。（板书：枚举法）‎ 师：还有其他的方法吗？（提示：在数的时候不能遗漏也不能重复）‎ 方法二（线段图）：‎ A B C D ‎ 说说你的想法:‎ 我是用线段图解决问题的，我分别用A、B、C、D表示小丽、小军、小杰、小阳四名同学，然后分别用不同颜色的弧线连接AB、AC、AD、BC、BD、CD. 一共有6条弧线，每条弧线段代表一种组队方案，所以有6种不同的组队方案。‎ 谈话：同学们，像我们刚才这样，把所有的可能，采用画线段图的方法一一用不同颜色的弧线连接起来，并最终找到答案的方法，叫画线段法。（板书：画线段法）‎ 方法三(平面图)‎ ‎ ‎ ‎ 小 丽 小 军 ‎ ‎ 小 杰 小 阳 说说你的想法:‎ 我是用平面图解决问题的，我用四个圆点分别表示小丽、小军、小杰、小阳，再分别用不同颜色的线段连接小丽——小军 ， 小丽——小杰，小丽——小阳，小军——小杰，小军——小阳，小杰——小阳。一共有6条线段，每条线段代表一种组队方案，所以有6种不同的组队方案。‎ 谈话：同学们，像我们刚才这样，把所有的可能，采用画平面图的方法一一用不同颜色的线段连接起来，并最终找到答案的方法，这种方法叫画平面图法。‎ ‎（板书：画平面图法）‎ ‎2.二次探究（课件出示）：‎ 如果从小丽、小军、小杰、小阳、小美5名同学中选出2人代表学校参加“少儿戏曲大赛”，有多少不同的组队方案？‎ 谈话：这个问题你们还能用刚才的办法解决吗？看看哪个小组最会合作。‎ 教师巡视。‎ 谈话：哪个小组愿意和大家一起交流？下面的同学请认真听，你有什么要补充的吗？‎ 预设：‎ 学生1：我用的是枚举法。实物展示：‎ ‎ 小军 小杰 小阳 小丽 小杰 小军 小阳 小杰 小阳 小美 ‎ 小阳 小美 小美 ‎ 小美  ‎ ‎ 我是先固定小丽同学，再分别与小军、小杰、小阳、小美组合，有四种组合；然后再固定小军同学，再分别与小杰、小阳、小美组合，有三种组合；接着固定小杰同学，再与小阳、小美组合，有两种组合。最后固定小阳同学，再和小美组合，有一种组合 。一共有10种组合，所以有10种不同的组队方案。‎ 学生2：我用的是画线段图。实物展示：‎ A B C D E 我用线段图分析，用A、B、C、D、E五个点分别代表小丽、小军、小杰、小阳、小美五名同学，然后分别用不同颜色的弧线连接AB、AC、AD、AE、BC、BD、BE、CD、CE、DE。‎ ‎ 一共有10条弧线，每条弧线段代表一种组队方案，所以有10种不同的组队方案。‎ 学生3：我用的是画平面图。实物展示：‎ ‎ 小丽 ‎ ‎ ‎ 小军 小美 ‎ 小杰 小阳 我是用平面图分析解决问题的，我用五个圆点分别表示小丽、小军、小杰、小阳、小美，再分别用不同颜色的线段连接小丽——小军 ，小丽——小杰，小丽——小阳，小丽——小美，小军——小杰，小军——小阳，小军——小美，小杰——小阳，小杰——小美，小阳——小美。一共有10条线段，每条线段代表一种组队方案，所以有10种不同的组队方案。‎ 梳理方法：‎ 谈话：“请同学们观察这几种方法，它们有什么共同点呢？”‎ 课件出示三种方法。‎ 学生思考，同桌交流。汇报。‎ ‎（都是先固定一名同学，与其余同学分别组合。）‎ 总结：同学们说的很对，无论是用哪一种方法，都是按从前往后的顺序先固定一名同学，与其余同学分别组合，思路是一样的，只是表示方法不同。在组队的时候，不管是按照哪种方法，只要做到不重复、不遗漏地把所有的可能列出来就可以，它并不受排列的顺序限制。‎ 谈话：那么如果我们用点来表示学生人数，用两点之间的线段表示一种组合方案，你能完成下表吗？课件出示：‎ 师：我们一起来观察这张表，如果是2个学生，就可以用一条线段来代表他们之间的关系，两点之间只有1条线段，那么就表示一种组合方案；如果是3个学生呢？就可以用三角形来代表三者间的关系，我们一起来数数，三点间一共有3条线段，记作：2+1；如果是4个学生呢？请各合作小组用同样的方法使着完成此表。‎ 各小组共同完成表格，并根据表中数据找一找有什么规律？‎ 学生自主探索，教师巡视。‎ 谈话：谁来交流你们的想法？‎ 小组派代表展示说明自己小组的发现。‎ ‎（如果是4个学生，就可以用四边形来代表四者间的关系，我们数了数，四点间一共有6条线段，记作：3+2+1；如果是5个学生，就可以用五边形来代表五者间的关系，我们数完后，五点间一共有10条线段，记作：4+3+2+1。）‎ ‎【设计意图】教师及时发挥主导作用，带领学生填表、找规律，学生才能顺利完成任务。一石激起千层浪，学生思维的火花被点燃。‎ 思考：如果是6人呢？10人呢？你能根据上表的规律找出他们的组队方案吗？‎ 预设：‎ ‎（1）如果是6人，组队方案有5+4+3+2+1=15种 ‎ (2) 如果是10人，组队方案有9+8+7+6+5+4+3+2+1=45种 四、抽象概括，总结提升 同学们，我们这节课通过了从不同人数中选2名学生参加“少儿戏曲大赛”的生活实例进行探究，对简单的组合知识进行了学习。同学们真是不简单啊，探索出了这么多好办法。像把所有的组合可能，采用列举的方法一一写下来，并最终找到答案的方法的枚举法。画线段图的方法也非常好，可以按从前往后的顺序，分别学生固定一个点，依次和其他同学进行组合，这样能做到不重复、不遗漏。通过画平面图的方法，再结合课本图表，同学们掌握了简单组合问题的解答规律。‎ 五、巩固应用，拓展提升 下面我们就用刚才所学习的方法，试一试能不能解决这个问题。‎ ‎1.课件出示自主练习1‎ 温馨提示：‎ ‎（1）认真读题，这可是解决好问题的第一步。‎ ‎（2）有多少种不同的选法？把你的思考过程写在练习本上，列出算式。‎ ‎（3）说说自己组合的方法。‎ ‎2.课件出示自主练习3‎ 温馨提示：‎ ‎（1）认真看图。自己独立思考。‎ ‎（2）把你的思考过程写在练习本上，列出算式。第二个图有多少个三角形，可以先把整个图形分成大小相似的两个三角形。再分别数每个三角形里包含多少个小三角形。‎ ‎（3）说说自己是怎样数的。‎ 学生汇报交流：‎ 我数出10个角。我是按照从上往下的顺序，分别固定一条边，再和其他的边分别进行组合，数出有几个角，最后再把所有的角加起来，4+3+2+1=10‎ 我数出12个三角形。我第一次先数上边的三角形。先固定一条边，再和其他的边分别进行组合成三角形，数出有几个三角形，最后再把所有的三角形加起来， 3+2+1=6。第二次把图形中间的横行去掉，得到一个大三角形，也是先固定一条边，再和其他的边分别进行组合，数出有几个三角形，最后再把所有的三角形加起来， 3+2+1=6。然后（3+2+1）×2=12‎ ‎【设计意图】这是一组紧密“联系生活”的巩固练习，每个层次层层递进，‎ 目的是让学生充分感悟数学知识的奥妙，体验正确运用数学知识解决问题后的成功的喜悦 ；同时将解决问题置于生活背景之下，使学生感受到了数学的价值，明白“数学源于生活，而又应该服务于生活”这一重要学习目的。‎ 板书设计： ‎ 简单的组合 枚举法 画线段图 画平面图 ‎1‎ ‎2+1=3‎ ‎3+2+1=6‎ ‎4+3+2+1=10‎ ‎5+4+3+2+1=15‎ 使用说明：‎ ‎1、教学反思：回味课堂，我感觉亮点之处有：‎ ‎（1）在本节课的教学设计中，我从生活中数学问题入手，以谈话的形式因提出一个组合问题，激发学生探究组合问题的兴趣，再引导学生，解决复杂问题，可以先从同类型的简单问题入手，探究出解决类似问题的方法。‎ ‎（2）注重解决问题方法的多样化，发展学生思维。  ‎ 不同的学生有不同的思维方式以及不同的发展潜能。教学中关注学生的这些个性差异，应允许学生存在思维方式的多样化和思维水平的不同层次。本节课我也给学生足够的时间和空间，鼓励学生大胆地发表自己的观点和想法。让学生用多种方法表示出思考过程。然后，组织全班交流，抽象总结出：枚举法、线段法、图形法。方法多样性之后，注重引导学生体会方法的共同点。新课改下的数学课不仅是让学生掌握固定的运算方法，也要发展学生的思维能力，让课堂焕发生命的活力。 ‎ ‎（3）在练习中，课堂上尊重学生的生成问题，让不同意见的学生大胆表达，在交流讨论中，学生能够充分体会按顺序组合的优点。‎ ‎2、使用建议。‎ 学生在思考组合方案时，教师要鼓励学生多说，学生说得越具体越好，教师注意引导总结，发现方法，形成知识技能。‎ ‎3、需破解的问题。‎ 在一般“组合”问题教学环节的设计上，我也有不足的地方，我局限于教材安排，目标定在学生能掌握简单组合问题的思考方法，对学生找规律，解答简单组合问题这方面没有处理好，对知识的处理、思维的培养上还不够。‎ ‎ ‎