人教版小学六年级下册数学课件第六单元整理和复习 课时7

人教版小学六年级下册数学课件第六单元整理和复习 课时7

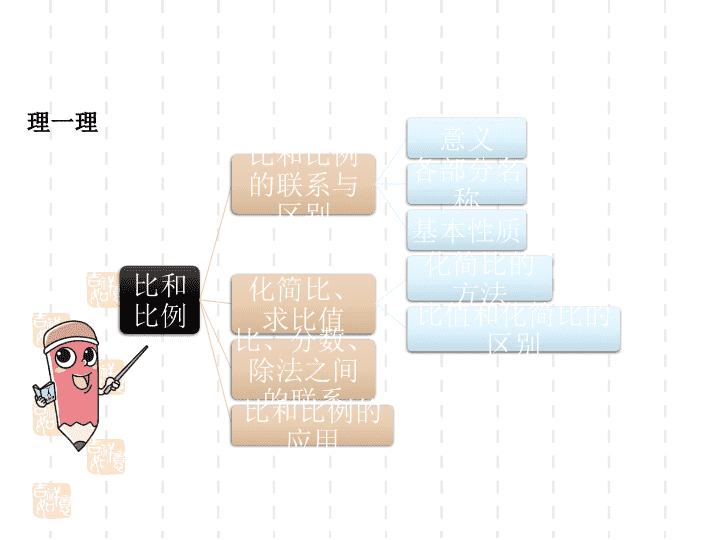
整理和复习第7课时数与代数 1.通过比较比和比例各部分名称和基本性质,深刻理解比和比例的意义,联系及区别。2.通过回顾正比例关系、反比例关系的概念,使学生正确掌握在生活事例中对于正比例和反比例的判断方法,在实际问题中能够灵活运用正比例和反比例解决问题。【重点】掌握比和比例的意义和性质。【难点】掌握在生活事例中对于正比例和反比例的判断方法。 理一理比和比例比和比例的联系与区别意义各部分名称基本性质化简比、求比值化简比的方法比值和化简比的区别比、分数、除法之间的联系比和比例的应用 比和比例的联系与区别比比例意义各部分名称基本性质两数相除又叫两个数的比。两个比相等的式子叫作比例。0.6：0.8=0.75前项后项比值………2:3=6:9内项外项比的前项和后项都乘或除以相同的数（0除外）比值不变。在比例里，两外项之积等于两内项之积。化简比的依据解比例的依据 化简比、求比值化简比的方法整数比小数比分数比比的前项和后项同时除以它们的最大公因数。把比前、后项的小数点向右移动相同的位数，转化成整数比再化简。把比前、后项同时乘分母的最小公倍数，转化成整数比再化简。 化简比、求比值一般方法结果求比值化简比根据比值的意义，用前项除以后项。结果是一个数，可以是整数、小数或分数。根据比的基本性质，把比的前项和后项都乘或者除以相同的数(零除外)。结果是一个比，而且是最简整数比。求比值和化简比的区别 比、分数、除法之间的联系及区别比除法分数联系区别前项后项比号比值被除数除号除数商分子分数线分母分数值比是两个数之间的倍数关系除法是一种运算分数是一种数 比、分数、除法之间的联系及区别比的基本性质、分数的基本性质、商不变的性质三者之间联系及区别比的基本性质分数的基本性质商不变的性质比的前项和后项同时乘或除以相同的数（0除外），比值不变。分数的分母和分子同时乘或除以相同的数（0除外），分数的大小不变。在除法中，被除数和除数同时乘或除以相同的数（0除外），商不变。商不变的性质、比的基本性质和分数的基本性质的内容实质上是一样的。 比和比例的应用比例尺分类举例意义一幅图的图上距离和实际距离的比。按表现形式，可以分为数值比例尺和线段比例尺。按将实际距离放大还是缩小分，分为缩小比例尺和放大比例尺。1：500000050km1：50000020：1 比和比例的应用解决按比分配问题的解题步骤01先找出或求出总数量和总份数（总数量是组成比的各个数量的和，总份数是各个比的和）。02再求出每份是多少。（总数量÷总份数）03用每份乘各部分数量所对应的份数。 名称联系区别变化规律关系式图像正比例反比例比和比例的应用正比例和反比例1.两种相关联的量。2.一种量随着另一种量的变化而变化。相对应的两个量的比值（商）一定。相对应的两个量的积一定。y:x=k(一定)xy=k(一定) 1(1)7÷8可以写成()。(2)()叫方程。含有未知数的等式(3)2∶4=()∶12。6(4)在比例里,两个内项的积是70,两个外项的积是()。70填空 判断下面两种量是否成比例,成什么比例?（1）爸爸上班的路程一定,速度和时间。（2）故事书的总页数一定,看的页数和剩余的页数。（3）单价一定,总价和数量。（4）三角形的面积一定,三角形的底与底边上的高。(1)成比例,成反比例(2)不成比例(3)成比例,成正比例(4)成比例,成反比例2 判断题(1)甲数除以乙数的商是1.4，甲数和乙数的比是7∶5。（）(2)π是圆的周长与直径的比值。（）(3)甲、乙两人同时从A地到B地，甲6小时到达，乙5小时到达。甲、乙所用的时间的比和速度的比都是6∶5。（）(4)在比例中，两个外项的积除以两个内项的积，商是0。（）(5)因为3×10=5×6，所以3:5=10:6。（）(6)18:30和3:5可以组成比例。（）√×√××√3 伦敦奥运会一块金牌的黄金含量与金牌总重的比为6：412。一块金牌总重412g，302块金牌需要黄金多少克？答：302块金牌需要黄金1812克。6(克)1812(克)4 北京到济南高速公路距离大约为430km，北京到天津大约为120km。一辆汽车从北京出发开往济南，当行驶到天津时用了1.5小时。按照这个速度，北京到济南全程需要多少小时？答：北京到济南全程需要5.375小时。解:设需要x小时。5 同一幅地图上，量得甲、乙两地的直线距离是20cm，甲、丙两地的直线距离是12cm。如果甲、乙两地的实际距离是1600km，那么甲、丙两地的实际距离是多少？答：甲、丙两地的实际距离是960km。解:设甲、丙两地的实际距离为xkm。6 六年级（2）班乘车去农家果园采摘草莓，汽车以40千米/时的速度行驶1小时到达果园，在果园活动了2小时，然后乘车以相同的速度返回。观察下面两幅图象，它们有什么不同？返回时汽车行驶的路程不断增加,而离校距离越来越近(少)，与来时的方向相反。7