人教版六年级上册数学第三单元分数除法 习题课件

人教版六年级上册数学第三单元分数除法 习题课件

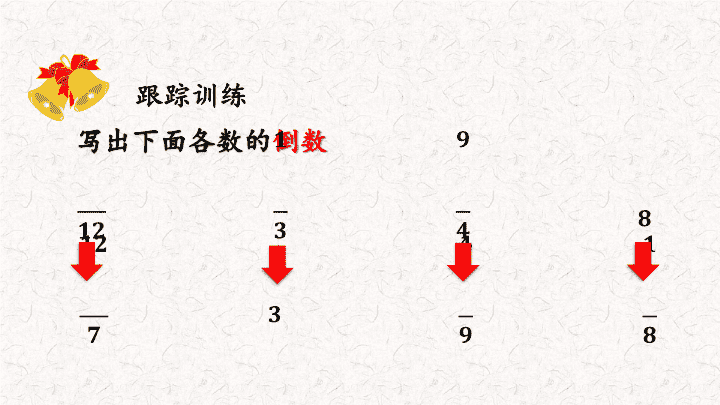
练习六 分数除法 3 人教版 六年级 数学 上册 倒数的认识 意义 特点 求倒数的方法 乘积是 1 的两个数互为 倒数。 将这个数的分子和分母调换位置 。 乘积是 1 。 分子、分母 颠倒位置。 1 的倒数是 1 ， 0 没有倒数。 跟踪训练 写出下面各数的 倒数 × （ ）＝ 1 × （ ）＝ 1 × （ ）＝ 1 × （ ）＝ 1 17 × （ ）＝ 1 × （ ）＝ 1 5 填一填。 跟踪训练 异口同声，抢答问题。 规则：两小组之间进行 PK 。相互为对方小组出题，对方小组在规定时间内回答出所给数字的倒数，并由老师倒数后齐声回答，然后交换问答方，往复进行，回答错误的小组视为淘汰。看看谁是最后的擂主！ 倒数是相互依存的 先把小数化成分数，再求倒数。 （ 1 ） × ＝ 1, 。 正确： 和 互为倒数。 （ 2 ） 2.5 的倒数是 。 正确： 2.5 的倒数是 。 × × 判断。 （ 3 ）一个数的倒数一定比这个数小。 （ 1 ） 与 的乘积为 1 ，所以 和 互为倒数。 （ 2 ） × × ＝ 1 ，所以 、 、 互为倒数。 ( ) ( ) ( ) √ × × 下面的说法对不对？ 倒数只是两个数间的关系 2 的倒数是 0.5,2 ＞ 0.5 。 小红和小亮谁说得对？ 正确 小红说得对。乘积是 1 的两个数就互为倒数，这两个数可以是分数，也可以是小数或整数。 写出符合下面要求的数。 （ 1 ）一个数的倒数在 和 之间，这个数可能是多少？ 答案不唯一 = = = = = = 写出符合下面要求的数。 （ 2 ）一个自然数与它的倒数的和是 5 , 这个自然数是多少？ 答：这个自然数是 5 。 x + = 5 设这个自然数为 x 。 x = 5 已知 ×A=B× =C, 并且 A 、 B 、 C 都不为 0 。请把这三个数 照从大到小的顺序排列。 假设 C=1 ，用倒数的知识解决。 A= A ＞ B ＞ C B= 1. 乘积是 1 的两个数互为倒数。 这节课你们都学会了哪些知识？ 2. 求分数的倒数的方法是 交换分子、分母的位置 。 3. 求整数和小数的倒数，可把整数看成 分母是 1 的分数，把小数化成分数，再求倒数。 练习七 分数除法 3 分数除法的计算法则 除以一个不等于 0 的数，等于乘这个数的倒数。 被除数不变 示 小 提 除法转化成乘法 除数转化成它的倒数 你能说一说分数除法的计算法则吗？ 跟踪训练 计算下面各数 × 5 13 ÷ ÷ = × = = 13 × = = × = 一盏节能灯 1 小时耗电 千瓦时，某个传达室除了这盏节能灯外，没有别的用电器。这个传达室上个月的用电量是 千瓦时，这盏节能灯上个月共使用多少小时 ？ 答：这盏节能灯上个月共使用 100 小时 。 =100( 小时） 分数四则混合运算 顺序 先乘除、后加减 。 有括号先算括号里的 。 只含乘除时，按从左到右顺序计算 。 计算下面各题。 跟踪训练 ） = = = = = 她们已经装完了多少袋？ 才装完了总量的 。 一共有 240kg 水果糖，每袋装 kg 。 答：她们已经装完了 720 袋。 240 =240 4 =720( 袋） 根据乘法算式写出两道除法算式。 （ ） = 填一填。 （ 3 ） 里有（ ）个 ， 是 的（ ）倍，（ ）的 是 。 （ 1 ） （ 2 ） = （ ） （ ） = （ ） 8 (1) 甲数除以乙数，等于甲数乘乙数的倒数。 ( ) (2) 一个非零自然数除以任何分数，商都大于被除数。 ( ) (3) 一个数除以 ，就相当于把这个数扩大到原来的 4 倍 。 ( ) (4) “÷ 2 ”和“× 2 ”的结果相同，意义也相同。 ( ) × × √ √ 判 断。 在⚪里填上“ > ”“ < ”或“ = ”。 > < < = > > 12÷ 12 ÷7 ÷ ÷ ÷ ÷ ⚪ ⚪ ⚪ ⚪ ⚪ ⚪ 芳芳将 m 长的丝带剪成同样长的 8 段，每段丝带有多长？ ÷8 ＝ （ m ） 答：每段丝带有 m 。 2019 年底，一种新型冠状病毒在我国肆虐开来，一个口罩生产工厂计划生产一批医用口罩用于支援奋战在一线的医生和护士，该工厂平均每个车间可生产口罩 2.5 万只，已经生产了这批订单口罩总数量的 ，共用 小时，平均每小时生产口罩多少只？ 2.5 × × 10000 =15000 （只） 1 5000 ÷ =7000 （只） 答：平均每小时生产口罩 7000 只。 某饮料厂使用一种自动检测仪来检测饮料瓶是否有缺陷，检测一个瓶子所用的时间为 秒。一分钟可以检测多少个瓶子？ 1 分钟＝ 60 秒 60÷ ＝ 60×25 ＝ 1500 （个） 答：一分钟可以检测 1500 个瓶子。 照这个速度，老爷爷每天慢跑要用多少时间？ 方法 1 ： 6÷ ＝ 12 （个） 2×12 ＝ 24 （分） 方法 2 ： 2÷ ＝ 4 （分） 4×6 ＝ 24 （分） 答：老爷爷每天慢跑要用 24 分。 半圈就是 圈 ; 半圈用 2 分钟，那么一圈用 4 分钟。 这幢楼共有 15 层，我家住 7 楼。 小萍家的地板离地有多高？ 7 楼楼板到地面的高度实际上只有 6 层楼的高度。 这幢楼共有 15 层，我家住 7 楼。 答：小萍家的地板离地有 20 米高。 小萍家的地板离地有多高？ 50÷15× （ 7-1 ） =50÷15×6 =50× ×6 =20 （米） 方法一 这幢楼共有 15 层，我家住 7 楼。 =50× =20 （米） 答：小萍家的地板离地有 20 米高。 方法二 15× （ 7-1 ） ÷15 6 层是 15 层的几分之几 小萍家的地板离地有多高？ 得数 = 原数 7 15 2 3 7 10 14 15 7 15 3 4 1 2 ÷ 按下面的步骤计算，将把最后的得数与开始的数比较，你能发现什么，你知道为什么吗？ ÷ × 2 3 ÷ ÷ 3 4 1 2 × 7 15 = 3 2 × 4 3 × 1 2 × 7 15 = × 1 7 15 1. 分数除法 的计算方法。 这节课你们都学会了哪些知识？ 2. 分数四则混合运算的 运算顺序 。 3. 只有乘、除法的分数四混合运算可以 改写成连乘 的形式使计算简便。 练习八 分数除法 3 已知一个数的几分之几是多少，求这个数 2 1 设单位 ”1” 的量为 x ，列方程解答。 已知量 ÷ 已知量占单位“ 1 ”的几分之几 = 单位“ 1 ”的量 你能说一说解决这类问题的方法吗？ 操场上打篮球的有4人。 打篮球的人数是踢足球人数的 ，踢足球的有多少人？ 解：设踢足球的有 x 人。 x = 9 答：有9人踢足球。 跟踪训练 4 x = x ÷ = 4 ÷ 已知比一个数多（或少）几分之几的数是多少，求这个数 2 1 找题中 单位“ 1’ 量 ，计算已知量占单位” 1 “的几分之几，再根据分数除法的意义列 除法 算式解答。 单位“ 1 ”的量 × （ 1± 几分之几） = 已知量或单位 “ 1 ”的量 ± 单位“ 1 ”的量 × 几分之几 = 已知量 跟踪训练 一种药品现在的售价是 12 元，价格比原来降低了 。 这种药品原价是多少元？ 解：设这种药品原价是 x 元。 答：这种药品原价是 72 元。 x = 72 x － = 12 x 单位“ 1 ” “ 1 ” 还剩 读了 35 页 ？页 这本课外读物一共有多少页？ 这本课外读物我读了 35 页，还剩下 没读。 35÷ （ 1- ） =35÷ =49( 页） 答：这本课外读物一共 49 页。 （ 1 ）图书馆共有多少本书？ 320÷ ＝ 800 （本） 答：图书馆共有 800 本书。 （ 2 ）图书馆有多少本故事书？ 320÷ ＝ 240 （本） 答：图书馆有 240 本故事书。 武汉火神山医院的建成，让世界的目光再一次聚焦到了中国，使他们再一次被 “ 中国速度 ” 所震撼！火神山医院是参照抗击非典期间北京小汤山医院模式建设，已知建成小汤山医院共花费 7 天的时间，比火神山医院用时少 ，建成火神山医院共用多少天？ 7 ÷（ 1- ） =10 （天） 答：建成火神山医院共用 10 天。 30 人 ？人 篮球队人数： 足球队人数： “ 1 ” 学校足球队一共有 30 人，比篮球队的人数多 ，篮球队有多少人？ 多 30÷ （ 1 ＋ ） =25( 人） 答：篮球队有 25 人。 找题中的等量关系，再列出方程。 西安到兰州的铁路长 676km ，比兰州到乌鲁木齐铁路长的 少 180km 。兰州到乌鲁木齐的铁路长多少千米？ 解：设兰州到乌鲁木齐的铁路长 x km 。 答：兰州到乌鲁木齐的铁路长 2568km 。 x =856 兰州到乌鲁木齐的铁路长的 － 180 = 676 x － 180=676 x = 2568 （ 1 ）大齿轮有 140 个齿，小齿轮的齿数是大齿轮的 。小齿轮有多少个齿？ 140× =28 （个） 答：小齿轮有 28 个。 单位“ 1 ”已知，用乘法计算。 有一组互相咬合的齿轮 （ 2 ）小齿轮有 28 个齿，是大齿轮的 。大齿轮有多少个齿？ 28÷ =140 （个） 答：大齿轮有 140 个齿。 单位“ 1 ”未知，用除法计算。 有一组互相咬合的齿轮 （ 3 ）小齿轮每分钟转 400 周，大齿轮每分钟转的周数比小齿轮少 。大齿轮每分钟转多少周？ 400× （ 1 - ） =80 （周） 答：大齿轮每分钟转 80 周。 有一组互相咬合的齿轮 有一组互相咬合的齿轮 （ 4 ）大齿轮每分钟转 80 周，比小齿轮每分钟转的周数少 。小齿轮每分钟转多少周？ 80÷ （ 1- ） =400 （周） 答：小齿轮每分钟转 400 周。 电脑公司要修 144 台电脑，已经修了这批电脑的 ，又送来一些电脑需要维修，这时已经修好的电脑占电脑总数的 ，又送来多少台电脑？ 解：设又送来 x 台电脑 。 x = 14 4 × (144 ＋ ） × x = 288 答：又送来 288 台电脑。 电脑总数前后发生变化，单位“ 1 ”也变了。 小提示 这节课你们都学会了哪些知识？ 列方程解决问题的方法 （ 1) 找单位“ 1 ” ，设 x ； （ 2 ）找 数量关系 ； （ 3 ） 列方程 ， 解方程 。 （ 4 ） 检验写答语 。 练习九 分数除法 3 解决含有两个未知量的分数应用题 方法 有 两个量 都是未知的，先把谁看作 单位“1” 都可以，设其中 一个量为未知数 x ，用这个量表示 另一个量 ，然后找出 等量 关系，列方程解答出一个量，再解答第二个量。 你能说一说解决问题的方法吗？ 跟踪训练 航模小组和美术小组分别有多少人？ 航模小组和美术小组一共有 45 人。 美术小组的人数是航模小组的 。 5 4 解：设航模小组有 人，则美术小组有 人。 x x x ＋ =45 x x =45 x =25 25× =20 （人） 答 : 航模小组有 25 人，美术小组有 20 人。 （ 1 ）把工作总量看作单位“ 1” 。 （ 2 ）解决工程问题的关键是用单位时间内完成工作总量的几分之一来表示工作效率 （ 3 ）工作总量 ÷ 工作效率之和 = 工作时间 工程问题 生活中，类似于修公路等问题，统称为“工程问题”。它是分数问题的特例，工作总量与工作效率都不是具体的数，而是用抽象的分数来表示。 挖一条水渠，王伯伯每天挖整条水渠的 ，李叔叔每天挖整条水渠的 。两人合作，几天能挖完？ 1÷ （ ） ＝ 1÷ ＝ 12 （天） 答：两人合作， 12 天能挖完。 跟踪训练 选择 （ 1 ）加工一批服装，甲组单独做每天完成 ，乙组单独做每天完成 ，两组同时加工多少天完成？正确列式是（ ） A. B.1÷ （ ） C.1÷ （ 1÷ ） B 选择 A. 360÷20+360÷30 B.360÷ （ － ） C （ 2 ）一个游泳池可装水 360 吨，单开进水管 20 小时注满水池，单开出水管 30 小时可把满池水放完，现在同时打开两管，几小时可把水池注满？正确列式是（ ）。 C.1÷ （ － ） 甲、乙两人打一篇稿件 , 甲单独打 ,5 天打完 , 乙单独打 ,6 天打完。两人合作 , 几天打完 ? 1÷ （ + ） =1÷ = ( 天） 答：两队合作， 天打完。 一项工程，甲队单独需要 小时，乙队需要 小时，两队合做，多少小时可以完成？ 1÷ （ 1÷ +1÷ ） = 1÷14 = ( 小时） 答：两队合作， 小时可以完成。 两个分数后边都有单位 “小时”，这两个分数是 工作时间而不是工作效率。 一共有 300 棵树，如果我们一队单独种，需要 8 天。 如果我们二队单独种，需要 10 天。 现在两队合种， 5 天能种完吗？ 1÷ （ 1÷8 +1÷10 ） =1÷ （ + ） = ( 天） ＜ 5 答：现在两队两队合种， 5 天能种完。 自新冠病毒爆发以来，口罩作为重要的防护物资一度售罄，某厂计划生产一批口罩用于支援一线医护人员。厂长把任务交给甲车间，甲车间主任说：“我们20天内刚好可以完成任务”。甲车间生产了5天后由于疫情危机，要求6天后送到一线医护人员手中，厂长于是把剩下的生产任务交给乙车间，乙车间主任说：“这些任务我们需要12天才能完成”，厂长决定让甲乙两个车间共同完成这些任务，请你算一算，他们能在6天内完成剩下的任务吗？ 甲的工作效率： 1 ÷ 20= 未完成的任 务： 1- = 乙的工作效率： ÷ 12= 共同完成需要的天数： ÷（ + ） = ＞ 6 答 : 不能完成。 中国农历中的“夏至”是一年中白昼最长、黑夜最短的一天。这一天，北京的黑夜时间是白天时间的 。白昼和黑夜分别是多少小时？ 你能找到题目中的隐含条件并解决问题吗？ 解：设白天的时间是 x 小时，黑夜的时间是 x 小时。 x ＋ x ＝ 24 x ＝ 24 x ＝ 15 15× ＝ 9 （小时） 答：白昼是 15 小时，黑夜是 9 小时。 一天一共有 24 个小时 也就是白昼＋黑夜＝ 24 小时 一个两位数，已知它的十位上的数是个位上的数的 。如果把这个两位数上的数与个位上的数交换位置，那么所得的新数就比原数大 27 。求原来这个两位数是多少。 新数 - 原数 =27 解：设原来这个两位数的个位上的数是 x 。 10 x ＋ x －（ x ×10 ＋ x ）= 27 x =9 十位上的数： 9× =6 所求两位数： 6×10 ＋ 9=69 答：这个两位数是 69 。 这节课你们都学会了哪些知识？ （ 1) 找单位“ 1 ” ； （ 2 ）找 数量关系 ；，含有两个未知量，找出如何用未知量表示另一个未知量 （ 3 ） 列方程 ， 解方程 。 （ 4 ） 检验写答语 。 练习十 分数除法 3 分数除法 计算方法 分数应用题 已知一个数的几分之几是多少， 求这个数。 已知比一个数多（少）几分之几 的数是多少，求这个数。 已知两个数的和（差）及这两个数的倍数关系求这两个数。 工程问题。 一个机械加工厂，九月份生产一种零件 1000 个，比原计划多生产 。原计 划 生产多少个零件？ 跟踪训练 解：设原计划生产 x 个零件。 答：原计划生产 800 个零件。 x ＋ =1000 x x =800 跟踪训练 解：设小麦有 x 吨。 x ＋（ 1 ＋ ） =390 x x =390 x =180 390 － 180=210 （吨） 答 : 大米有 210 吨，小麦有 180 吨。 仓库有大米和小麦共 390 吨，大米比小麦多 ，仓库有大米、小麦各多少吨？ 跟踪训练 一份稿件，甲每小时打这份稿件的 ，乙单独打完这份稿件要 6 小时。如果两人合打这份稿件，几小时才能完成这份稿件的 ? ＝ 3 （小时） （ ＋ ） ＝ ÷ ÷ （ ＋ 1÷6 ） 答： 3 小时才能完成这份稿件的 。 填一填。 （ 1 ） 40÷ =40× （ ） 36÷ =36× （ ） （ 2 ） 16 的 是（ ）；一个数的 是 15 ，这个数是（ ）。 （ 3 ）甲数是乙数的 ，就是把（ ）看作单位“ 1 ”，平均分成（ ）份，甲数相当于这样的（ ）份。 10 24 2 乙数 5 8 判断 （ 1 ）两个分数相除，商一定大于被除数。 ( ) （ 2 ）如果 a÷b= ， b 就是 a 的 3 倍。 ( ) （ 3 ）如果 a÷b= ，那么 a=3 ， b=5 。 ( ) × × √ 1 － ÷ （ ＋ ） × = － × 1 = 1 － = 计算下面各题 = × ＋ × = ＋ = 冰融化成水后，水的体积是冰的体积的 。现有一块冰，融化成水以后的体积是 30dm 3 ，这块冰的体积是多少立方分米？ 30÷ =33 （ dm 3 ） 已知一个数的几分之几是多少求这个数用除法计算 答：这块冰的体积是 33 立方分米。 解：设这块冰的体积是 x 立方分米。 x 11 10 =30 x =33 答：这块冰的体积是 33 立方分米。 冰融化成水后，水的体积是冰的体积的 。现有一块冰，融化成水以后的体积是 30dm 3 ，这块冰的体积是多少立方分米？ 狮子奔跑时的最高时速可以达到 60 千米 / 时，比猎豹慢 。猎豹奔跑时的最高时速是多少？ 单位“ 1 ”未知，用除法计算。 60÷(1- ) =60÷ =110 （千米 / 时） 答：猎豹奔跑时的最高时速是 110 千米 / 时。 小明和爷爷一起去操场散步。小明走一圈要 8 分钟，爷爷走一圈需要 10 分钟。 （ 1) 如果两人同时同地出发，相背而行，多少分钟后相遇？ 把两人共同行走的路程看作单位“ 1 ”， 用路程除以速度和就是相遇时间 1÷ （ 1÷8 ＋ 1÷10 ） ＝ 1÷ ＝ （分） 答：如果两人同时同地出发，相背而行， 分钟后相遇。 （ 2) 如果两人同时同地出发，同方向而行，多少分钟后小明超出爷爷一整圈？ 把超出一整圈看作单位“ 1 ”，用路程除以速度差就是所用时间 1÷ （ 1÷8 － 1÷10 ） ＝ 1÷ ＝ （分） 40 答：如果两人同时同地出发，相背而行， 分钟后相遇。 40 小明和爷爷一起去操场散步。小明走一圈要 8 分钟，爷爷走一圈需要 10 分钟。 北京大兴国际机场，是建设在北京市大兴区与河北省廊坊市广阳区之间的超大型国际航空综合交通枢纽。为了配合机场运营，某地准备建设一批相关配套设施，如果把建设工作分给甲、乙两队合作完成，则要36天完成，乙、丙两队合作要45天完成，甲、丙两队合作要60天完成。那么甲队独做需要多少天完成？ 甲、乙两队的工作效率： 1 ÷ 36= 乙、丙两队的工作效率： 1 ÷ 45= 甲、丙两队的工作效率： 1 ÷ 60= 甲队的工作效率：（ + - ）÷ 2= 甲单独做需要： 1 ÷ =90 （天） 答： 甲队独做需要 90 天完成 。 1. 根据数据的特点灵活运用方法，使计算简便。 这节课你们都学会了哪些知识？ 2. 用方程解答实际问题时，关键是找准单位“ 1 ”，再找出数量间的相等关系，并列出方程。