五年级上册数学课件-5解简易方程

五年级上册数学课件-5解简易方程

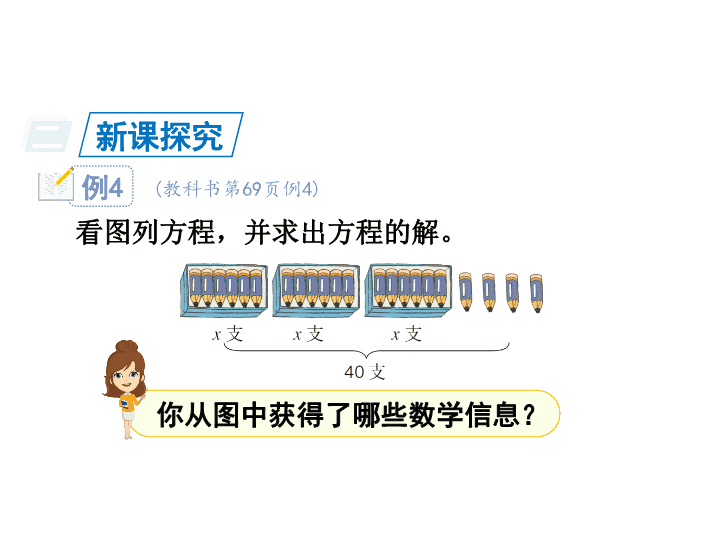
简易方程 人教版五年级数学上册 2 解简易方程 第 6 课时 解稍复杂的方程 5 一 复习导入 后面括号中哪 个 x 的值是方程的解？请画“√”。 （ 1 ） 8 x = 24 （ x = 2. 5 ， x = 3 ） （ 2 ） 1 8+ x = 29 （ x = 11 ， x = 47 ） （ 3 ） x ÷ 4= 0.2 （ x = 20 ， x = 0.8 ） （ 4 ） 6.3 ÷ x = 7 （ x = 0.9 ， x = 9 ） 二 新课探究 ( 教科书第 69 页例 4) 例 4 看图列方程，并求出方程的解。 你从图中获得了哪些数学信息？ 盒子里的铅笔数 量 列式： 3 x +4= 40 + 盒子外的铅笔数 量 = 铅笔总数量 你会算吗？ 3 x +4= 40 3 x + 4 − 4= 4 0 − 4 3 x = 36 3 x ÷ 3= 36 ÷ 3 x = 12 解： 解法分析 你算对了吗？ 先 把 3 x 看成一个整体，求出“ 3 x ”，最后 求 x 。 ( 教科书第 69 页例 5) 例 5 解方 程 2 （ x − 16 ） = 8 。 2 （ x − 16 ） = 8 2 （ x − 16 ） ÷ 2= 8÷ 2 x − 1 6= 4 x − 1 6 + 1 6 = 4+ 16 x = 20 请你自己把这个方程解完。 把什么看成一个整体？ 把括号内“ x − 16 ”看成一个整体，先求出“ x − 16 ”的值再求 出 x 。 x − 16 解： 也可以这样解： 2 x − 3 2= 8 2 x − 3 2+ 3 2= 8+ 32 2 x = 40 2 x ÷ 2= 40÷2 x = 20 解： 运用了什么运算定律？ 乘法分配律 方程左 边 = 2 （ x − 16 ） = = = 方程右边 2 × （ 2 0− 16 ） 2 ×4 所 以 x = 2 0 是方程的解。 别忘了检验！ 三 随堂练习 1. 看图列方程，并求出方程的解。 5 x + 1. 5= 7.5 x = 1.2 x 元 / 本 1. 5 元 7. 5 元 （教科书 第 69 页做一做） 2. 解下列方程。 （教科书 第 69 页做一做） 6 x − 3 5= 13 3 x − 12× 6= 6 x = 8 x = 2 6 （ 5 x − 12 ） × 8= 24 x = 3 （ 10 0 −3 x ） ÷ 2= 8 x = 28 6 x − 3 5= 13 6 x − 3 5+ 3 5= 1 3+ 35 3 x − 12× 6= 6 3 x − 7 2= 6 x = 8 6 x = 48 6 x ÷ 6= 48÷ 6 x = 2 6 3 x − 7 2+ 7 2= 6+ 72 3 x = 78 解： 解： 返回 （ 5 x − 12 ） × 8= 24 （ 5 x − 12 ） × 8 ÷ 8= 24÷ 8 x = 3 5 x − 12 = 3 5 x = 15 解： 返回 （ 10 0 −3 x ） ÷ 2= 8 （ 10 0 −3 x ） ÷2× 2= 8× 2 10 0 = 1 6+3 x 10 0 −3 x = 16 10 0 −3 x +3 x = 1 6+3 x 解： 1 6+3x− 1 6 = 10 0− 1 6 1 6+3 x= 10 0 返回 3 x ÷ 3= 84÷3 3 x = 84 x = 28 四 培优训练 1. 看图列方程，并解答。 x 元 / 个 748. 5 元 11 2 元 / 个 5 x + 112× 3= 748.5 x = 82.5 350 105 x x 105 2 （ 10 5 + x ） = 350 x = 70 2. 方 程 ɑ x + 2. 5= 2.9 5 与 7 （ x − 0.15 ） = 1.0 5 的解相 同， 求 ɑ + 3.7 8 的值。 7 （ x − 0.15 ） = 1.0 5 ɑ x + 2. 5= 2.9 5 x = 0.3 ɑ= 1.5 ɑ+ 3.7 8= 1. 5+ 3.7 8= 5.28 所 以 ɑ + 3.7 8 的值 是 5.2 8 。 五 课堂小结 如解形 如 b（ x ± ɑ ） = c 的方程，可以把 （ x ± ɑ ） 看作一个整体，先求出这个整体是多少 ， 再 求 x 是多少 ； 或利用乘法分配律将其化 为 b x ± ɑ b= c 的形式，再解方程。 形 如 ɑ x b=c 的方程的解法： 解： ɑ x b b=c b ɑ x =c b ɑ x ÷ ɑ = （ c b ） ÷ ɑ x = （ c b ） ÷ ɑ 解稍复杂的方程时，要灵活运用等式的基本性质求解。 课后作业 1. 从课后习题中选取； 2. 完成练习册本课时的习题。