五年级上册数学课件-3因数和倍数

五年级上册数学课件-3因数和倍数

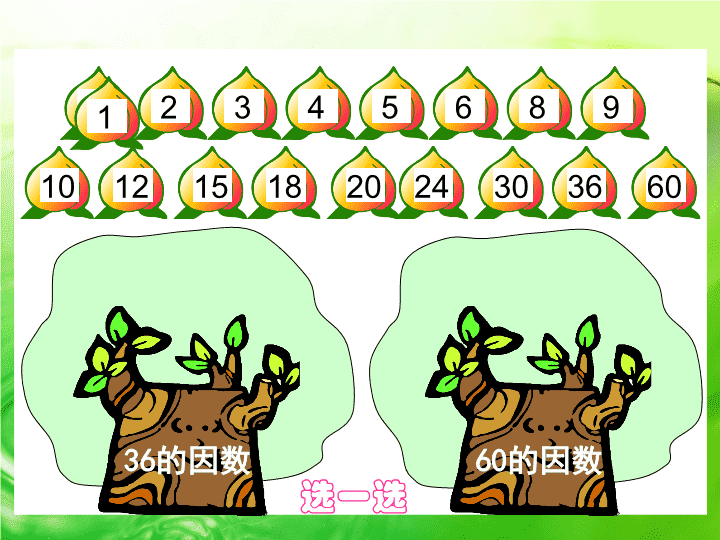
因数和倍数 　　规则：老师出一个数，看你卡片上的数是否符合条件，符合的请站起来 , 举起你的卡片上 , 看谁反应快 ? 我是 5 ，我找我的倍数。 我是 24 ，我找我的因数。 我是 30 ，我找我的因数。 我是 1 ，我找我的倍数。 轻松游戏: 36 的因数 60 的因数 选一选 12 15 18 20 24 30 36 60 10 5 8 9 2 2 1 1 3 3 4 4 6 6 12 知识导入 （一）因数与倍数： 如果 a × b=c （ a 、 b 、 c 都是非0的自然数，那么 和 就是 的因数， 就是 和 的倍数）.例如 3 × 4=12 ， 是 的倍数， 也是 的倍数， 4 和3都是12的 . a b c c a b 12 3 12 4 因数 （二）因数的特点： 一个数的因数的个数是 的，其中最小的因数是 最大的因数是 . 有限 1 它本身 （三）倍数的特点： 一个数的倍数的个数是 的，其中最小的倍数是 ， 最大的倍数. 2的倍数： ； 3的倍数： ； 5的倍数： . 无限 它本身 没有 个位上是0，2，4，6，8的数 各个数位上的数字和是3的倍数 个位上是0或5的数 例1、优胜路小学五年级（ 4 ）班48名学生参加体操表演，要求排成长方形队形，每行或每列不得少于3人，如果你是体育委员，你会怎么排列队形，共有多少种排列方法？ 王牌例题①: ∵ 每行或每列不得少于 3 人 ∴ 行列分别是 3 行 16 列 16 行 3 列 4 行 12 列 12 行 4 列 6 行 8 列 8 行 6 列 ∴ 共有 6 种排列方法。 答： 共有 6 种排列方法。 总结：先找总人数（总量）的所有因数，再根据条件一一讨论所有因数的可能性 1. 把64个玻璃球装在盒子里，每个盒子装得同样多，刚好装完，要求每个盒子里的玻璃球不得少于3个，问：共有多少种不同的装法？ ∵ 每个盒子的玻璃球不得少于 3 个 ∴ 每个盒子里可装 64 个共 1 个盒子 32 个共 2 个盒子 16 个共 4 个盒子 4 个共 16 个盒子 8 个共 8 个盒子 ∴ 共有 5 种不同的装法。 答： 共有 5 种不同的装法。 例2、某一个数可以写成 ，这个数有很多因数，全部的因数有 个？在这些因数中最小的因数是 ？最大的因数是 ？两位因数有 ？ 王牌例题②: 分析：这个数的因数可以由 3 与 5 组成， x 的因数最小为 1 ，依次是一个 3 ，一个 5 ，两个 3 的积，一个 3 与 5 的积。 9 1 225 75 、 45 、 25 、 15 总结：数因数个数时，因数从小到大数；找两位因数时，从大到小找 . 2. 某一个数可以写成 ，这个数有很多因数，全部的因数有 个？在这些因数中最小的因数是 ？最大的因数是 ？两位因数有 ？ 12 1 84 84 、 42 、 28 、 21 、 14 、 12 例3、一个数是40的因数，同时又是5的倍数，这个数可能是多少？ 王牌例题③: ∵5 的倍数中不大于 40 的有 5 、 10 、 15 、 20 、 25 、 30 、 35 、 40 40 的因数有 1 、 2 、 4 、 5 、 8 、 10 、 20 、 40 ∴ 既是 40 的因数，又是 5 的倍数的数有： 5 、 10 、 20 、 40 答： 这个数可能是 5 、 10 、 20 、 40 。 3. 一个数既是36的因数，又是4的倍数，这个数可能是多少？ ∵4 的倍数中不大于 36 的有 4 、 8 、 12 、 16 、 20 、 24 、 28 、 32 、 36 36 的因数有 1 、 2 、 3 、 4 、 6 、 9 、 12 、 18 、 36 ∴ 既是 36 的因数，又是 4 的倍数的数有： 4 、 12 、 36 答： 这个数可能是 4 、 12 、 36 。 例4、猜电话号码0371-A B C D E F G,提示： A是5的最小倍数 B是最小的自然数 C是5的最大因数 D既是4的倍数又是4的因数 E的所有因数是1、2、3、6 F的所有因数是1、3 G只有一个因数 问：这个电话号码是多少？ 王牌例题④: 5 0 5 4 6 3 1 ∵A=5 、 B=0 、 C=5 、 D=4 、 E=6 、 F=3 、 G=1 ∴ 电话号码为 0371-5054631 答： 这个电话号码是 5054631 。 例 5 、 (1)用0、3、4组成的各位数字互不相同的三位数，其中2的倍数有 ，既是2的倍数又是5的倍数的有 ； (2)五个连续自然数的和是120，那么其中最小的是 ； 王牌例题⑤: （ 1 ） ∵ 百位上不能为 0 、且三位数为 2 的倍数 ∴ 百位上可以放 3 或 4 ，个位上只能放 0 或 4 ∴ 这样的三位数 个位为 0 时有： 340 、 430 个位为 4 时有： 304 340 、 430 、 304 ∵5 的倍数个位是 0 或 5 ，同时是 2 的倍数 ∴ 三位数的个位数只能为 0 ∴ 这样的三位数有 340 、 430 （ 2 ） ∵ 中间的数为 120 ÷ 5=24 ∴ 最小的数为 24-2=22 340 、 430 22 例 6 、 有个四位数 同时是2、3和5的倍数，那么这个四位数最大是多少？最小是多少？ 王牌例题⑥: 答： 这个四位数最大是 6390 ，最小是 6300 。