- 2021-12-23 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
五年级下册数学单元测试-3长方体和正方体 冀教版 (含答案)
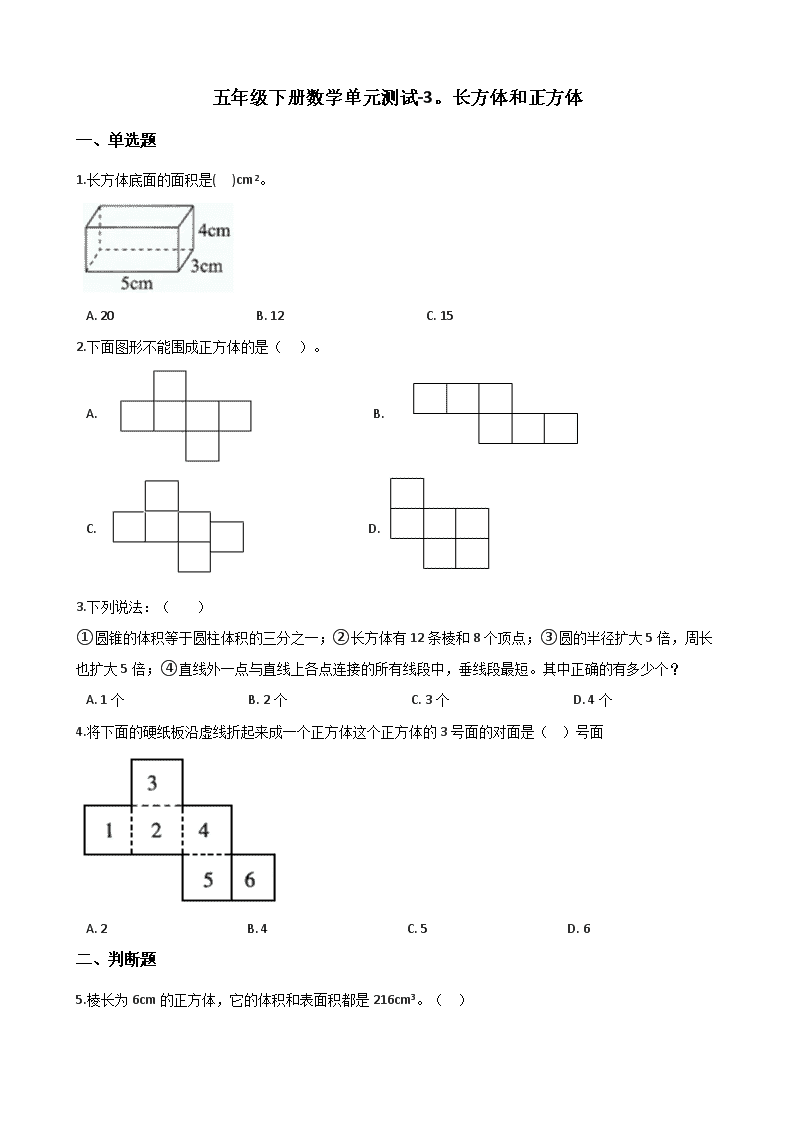
五年级下册数学单元测试-3。长方体和正方体 一、单选题 1.长方体底面的面积是( )cm2。 A. 20 B. 12 C. 15 2.下面图形不能围成正方体的是( )。 A. B. C. D. 3.下列说法:( ) ①圆锥的体积等于圆柱体积的三分之一;②长方体有 12 条棱和 8 个顶点;③圆的半径扩大 5 倍,周长 也扩大 5 倍;④直线外一点与直线上各点连接的所有线段中,垂线段最短。其中正确的有多少个? A. 1 个 B. 2 个 C. 3 个 D. 4 个 4.将下面的硬纸板沿虚线折起来成一个正方体这个正方体的 3 号面的对面是( )号面 A. 2 B. 4 C. 5 D. 6 二、判断题 5.棱长为 6cm 的正方体,它的体积和表面积都是 216cm3。( ) 6.如果一个长方体的棱长总和是 36cm,那么这个长方体相交于一个顶点的三条棱的长度之和是 9cm。( ) 7.长方体最多有 4 个面是正方形。 ( ) 8.体积相等的长方体,表面积一定相等。( ) 三、填空题 9.算出右图长方体中上、下、前、后、左、右六个面的面积分别是多少? 上面是________平方分米;下面是________平方分米; 前面是________平方分米;后面是________平方分米; 左面是________平方分米;右面是________平方分米. 10.如图所示,这个长方体的棱长总和是________cm。如果把它锯成两个长方体,并使表面积之和增加 24cm2 , 可以怎样锯,请在图中画出示意图。________ 11.用 3 个棱长 4 分米的正方体粘合成一个长方体,长方体的表面积是________平方厘米,体积是________ 立方厘米。 12.一个正方体的表面积是 24 平方厘米,它的体积是________。 四、解答题 13.现要用彩带捆扎一个长方体礼盒(如图),结头处的彩带长 40 厘米,捆扎一个这样的礼盒至少需要多 少厘米彩带? 14.一间长方体库房,长 5m、宽 4m、高 3m,在房顶和四面刷油漆(门窗忽略不计),刷油漆的面积是多 少平方米? 五、应用题 15.一块正方体魔方的棱长是 8 厘米,它的表面积是多少? 参考答案 一、单选题 1.【答案】 C 【解析】【解答】5×3=15(cm2). 故答案为:C. 【分析】根据题意,要求长方体的底面的面积,用长×宽=长方体的底面的面积,据此列式解答. 2.【答案】 D 【解析】【解答】解:D 选项中的展开图重新组合后会有重叠的面,这个图形不能围成正方体. 故答案为:D 【分析】判断能不能组成正方体,可以把任意一个面作为底面,然后确定其它面组合后有没有重叠的面, 如果有重叠的面就不能组成正方体,如果没有重叠的面就能组成正方体. 3.【答案】 C 【解析】【解答】①根据圆柱和圆锥的体积公式可得:等底等高的圆锥的体积是圆柱的体积的三分之一, ①错误; ②根据长方体的特点可得长方体有 12 条棱长,有 8 个顶点,②正确; ③根据圆的周长=2πr,其中 2π是一个定值,当 r 扩大 5 倍时,根据积的变化规律可得圆的周长也会扩大 5 倍,③正确; ④直线外一点与直线上各点连接的所有线段中,垂线段最短,是公理,④正确; 所以正确的有 3 个. 故答案为:C. 【分析】根据圆柱和圆锥的体积公式可知,等底等高的圆锥的体积是圆柱的体积的三分之一,只有在等底 等高的体积下,才能说圆锥体积是圆柱体积的三分之一;长方体的特征是:6 个面,12 条棱,8 个顶点; 圆的周长公式:C=2πr,半径 r 扩大或缩小几倍,周长也扩大或缩小相同的倍数;根据点到直线的距离可知, 直线外一点与直线上各点连接的所有线段中,垂线段最短,据此判断. 4.【答案】 C 【解析】【解答】解:这个正方体的 3 号面的对面是 5 号面。 故答案为:C。 【分析】如果是 2 号为底面,则 1 号是左面,4 号是右面;3 号是后面,5 号是前面;6 号是上面。由此确 定相对的面即可。 二、判断题 5.【答案】 错误 【解析】【解答】体积是表示物体所占空间的大小,它的常用单位有:m³,dm³,cm³····;面积是指一个平 面图形表面的大小,它的常用单位有:m²,dm²,cm²·····;它们的意义不同,单位不同。 故答案为:错误。 【分析】根据体积与面积的定义和单位进行判断。表面积不能用体积单位。 6.【答案】 正确 【解析】【解答】36÷4=9(cm),所以原题说法正确。 故答案为:正确。 【分析】长方体的每一个矩形都叫做长方体的面,面与面相交的线叫做长方体的棱,三条棱相交的点叫做 长方体的顶点,相交于一个顶点的三条棱的长度分别叫做长方体的长、宽、高。长方体有 12 条棱,相对 的四条棱长度相等。按长度可分为三组,每一组有 4 条棱,即(长+宽+高)×4=棱长总和。 7.【答案】错误 【解析】【解答】解:因长方体是 4 个面都是长方形,两个面是正方形,故错误。 故答案为:错误。 【分析】长方体共有 6 个面,有一组对面是正方形,有两组对面是相同的长方形,否则不能组合成长方体; 如果有 4 个面是正方形,不能组成长方体,一定是正方体。据此可求解。 8.【答案】 错误 【解析】【解答】体积相等的长方体,表面积不一定相等,原说法错误。 故答案为:错误。 【分析】长方体的体积=长×宽×高,长方体的表面积=(长×宽+长×高+宽×高)×2,体积相等说明长、宽、 高的乘积相等,但表面积不一定相等。 三、填空题 9.【答案】 15;15;20;20;12;12 【解析】【解答】 , 上面是 5×3=15 平方分米;下面是 5×3=15 平方分米; 前面是 5×4=20 平方分米;后面是 5×4=20 平方分米; 左面是 4×3=12 平方分米;右面是 4×3=12 平方分米. 故答案为:15;15;20;20;12;12. 【分析】长方体的 6 个面都是长方形,相对的两个面的面积相等,上面或下面的面积=长×宽,前面或后面 的面积=长×高,左面或右面的面积=宽×高,据此列式解答. 10.【答案】 60; 【解析】【解答】(8+4+3)×4 =15×4 =60(cm) 24÷2=12(cm2) 12=4×3 作图如下: 故答案为:60; 。 【分析】已知长方体的长、宽、高,求长方体的棱长总和,用公式:长方体的棱长总和=(长+宽+高)×4, 据此列式解答; 将这个长方体锯成两个长方体,表面积会增加两个截面的面积,增加的面积÷2=一个截面的面积,然后判 断怎么锯,据此作图。 11.【答案】 22400;192000 【解析】【解答】4×3=12(分米) 长方体的表面积: (12×4+12×4+4×4)×2 =(48+48+16)×2 =112×2 =224(平方分米) =22400(平方厘米) 长方体的体积: 12×4×4 =48×4 =192(立方分米) =192000(立方厘米) 故答案为:22400;192000。 【分析】 用 3 个棱长 4 分米的正方体粘合成一个长方体,长方体的长是 4×3=12 分米,宽是 4 分米,高 是 4 分米;已知长方体的长、宽、高,求长方体的表面积,用公式:长方体的表面积=(长×宽+长×高+宽× 高)×2,求长方体的体积,用公式:长方体的体积=长×宽×高,据此列式解答,注意:单位要换算。 12.【答案】 8 立方厘米 【解析】【解答】正方体一个面的面积:24÷6=4(平方厘米), 正方体的棱长为 2 厘米,它的体积是: 2×2×2 =4×2 =8(立方厘米). 故答案为:8 立方厘米. 【分析】已知正方体的表面积,求正方体的体积,先求出正方体的棱长,用正方体的表面积÷6=一个面的 面积,根据一个面的面积=棱长×棱长,可以求出正方体的棱长,然后用公式:正方体的体积=棱长×棱长× 棱长,据此列式解答. 四、解答题 13.【答案】 解: (厘米) 答:需要 140 厘米彩带。 【解析】【分析】根据题意可知,用长×2+宽×2+高×4+结头处的彩带长度=一共需要的彩带长度,据此列式 解答. 14.【答案】 解:房顶:5×4=20(平方米) 前后:5×3×2=30(平方米) 左右::4×3×2=24(平方米) 总面积:20+30+24=74(平方米) 答:刷油漆的面积是 74 平方米。 【解析】【分析】刷油漆的面积一共是 5 个面的面积,长方体上面的面积+前后左右的面积=刷油漆的面积; 长×宽=上面的面积,长×高×2=前后面的面积;宽×高×2=左右面的面积。 五、应用题 15.【答案】 解:8×8×6=384(平方厘米) 【解析】【解答】 8×8×6 =64×6 =384(平方厘米). 答:它的表面积是 384 平方厘米. 【分析】已知正方体的棱长,要求它的表面积,用公式:正方体的表面积=棱长×棱长×6,据此列式解答.查看更多