五年级上册数学教案-6 梯形的面积｜冀教版 (4)

五年级上册数学教案-6 梯形的面积｜冀教版 (4)

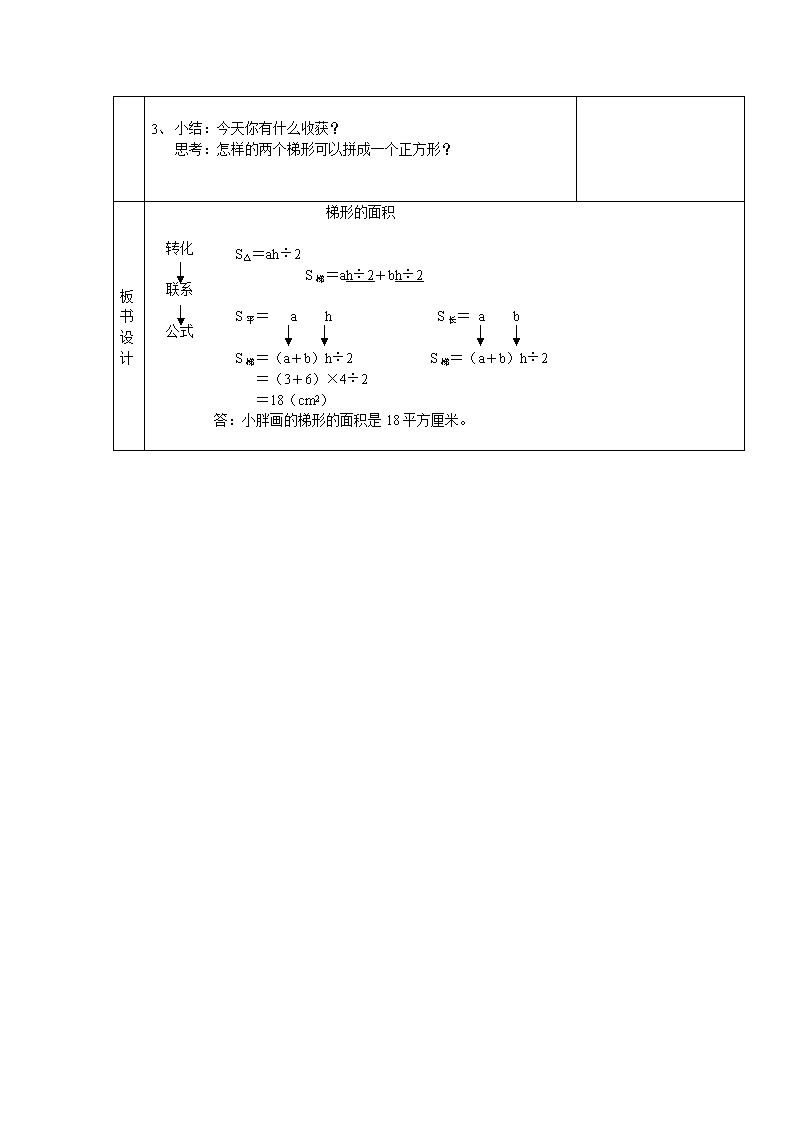
‎《梯形的面积》教学设计 教学目标 知识与技能：知道梯形的面积公式，‎ 会用公式正确计算梯形的面积。‎ 过程与方法：利用迁移规律，鼓励学生运用学具进行自主探究，推导出梯形的面积公式 。‎ 情感与态度：通过小组合作学习，培养学生团结协作、‎ 勇于创新的精神。‎ 教学重点：理解并掌握梯形面积公式的计算方法。‎ 教学难点：理解梯形面积公式的推导过程。‎ 教学准备：每个学生分别准备两个完全一样的一般梯形和两个完全一 样的直角梯形。‎ 设计说明 教学过程 一、复习引入：‎ ‎1、小巧和小亚谁画的图形的面积比较大?‎ 小巧： 小亚：‎ ‎ 小胖说：“我一看数据就知道小巧画的三角形的面积比较大。”‎ ‎ 同学们，你们认为呢？‎ ‎2、回顾三角形、平行四边形的面积公式推导过程：‎ 1) 计算三角形面积时，为什么底×高后要除以2？‎ 2) 平行四边形的面积公式又是怎样推导的？‎ 3) 板书：板书三角形、平行四边形的面积公式 ‎“转化――联系――公式”‎ ‎3、小丁丁也画了个梯形，他画的图形的面积有多大？‎ ‎（板书：梯形的面积）‎ 二、新授探究：‎ 1、 你准备把这个梯形转化成哪个我们学过的图形来计算它的面积？‎ ‎（生：正方形、长方形、三角形、平行四边形）‎ 2、 探究一：分成二个三角形进行计算 1） 学生独立尝试 ‎ 创设问题情景，复习已有知识，激发学习兴趣。‎ 回顾平行四边形、三角形面积公式及其推导的过程，为推导梯形的面积公式作迁移铺垫。‎ 出示小丁丁画的梯形，引入课题，激发学生的探究欲望 学生先猜测，再验证，培养学生的科学探究方法。‎ ‎2) 指名反馈 ‎3) 如果梯形的上底用a表示，下底用b表示，高用h表示，这个梯形的面积公式会是什么呢？‎ ‎（独立思考、同桌互说、全班交流）‎ 板书：s＝ah÷2＋bh÷2‎ ‎3、探究二：梯形转化成平行四边形 1) 怎样把梯形转化成平行四边形呢？‎ 2) 学生把2个完全相同的梯形在方格纸上拼一拼。‎ ‎（学生上台展示）‎ ‎ 3）思考：‎ A. 你所拼成的平行四边形的面积怎样计算？用含有字母的式子表示。‎ B. 每个梯形的面积又该怎样表示？‎ ‎（学生独立思考写一写，再小组内交流各自的想法）‎ 从学生最近发展区出发，改变课本上探究的顺序，放手让学生先用2个三角形的面积计算出梯形的面积。再用字母抽象出计算公式。‎ 每位学生都动手拼一拼，感悟二个完全相同的梯形可以拼成一个平行四边形。‎ 通过独立思考、小组合作交流等形式，培养学生的团结协作和创新能力。‎ ‎ 4) 全班交流：得出梯形的面积公式：‎ s＝（a＋b）h÷2‎ ‎4、前面二个梯形面积公式的区别和联系。‎ ‎5、利用公式s＝（a＋b）h÷2，计算小丁丁画的梯形的面积。‎ ‎ （板书计算过程）‎ 三、巩固深化：‎ ‎1、计算小胖画的梯形的面积：（单位：cm）‎ 1) 学生独立练习反馈 2) ‎（2＋3）×2.4表示什么呢？‎ 3) 这样两个完全相同的直角梯形是不是只能拼成一个平行四边形？（学生在方格纸上拼一拼：两个完全一样的直角梯形还可以拼成一个长方形）‎ 4) 怎样利用长方形的面积公式推导出梯形的面积公式？‎ 板书：长方形的面积＝长 × 宽 梯形的面积＝（a+b）×h÷2‎ ‎2、哪个梯形的面积比较大？（单位：dm）‎ 小巧： 小亚：‎ 利用乘法巧算的方法，把h÷2看做一个因数，把二个三角形计算公式归并到梯形面积公式。‎ 利用梯形面积公式计算直角梯形的面积，一方面让学生知道梯形的面积公式适合任何形状的梯形，另一方面又通过二个完全相同的直角梯形拼成一个长方形，通过长方形的面积也可推导出梯形的面积。‎ 及时巩固利用梯形的面积公式计算梯形面积的方法。梯形的形式有了些变化，特别是第二题要正确找出梯形的上底、下底、高等相关数据。‎ 1、 小结：今天你有什么收获？‎ 思考：怎样的两个梯形可以拼成一个正方形？‎ 板书设计 ‎ 梯形的面积 转化 联系 公式 ‎ ‎ ‎ S△＝ah÷2‎ ‎ S梯＝ah÷2＋bh÷2‎ ‎ S平＝ a h S长＝ a b S梯＝（a＋b）h÷2 S梯＝（a＋b）h÷2‎ ‎ ＝（3＋6）×4÷2‎ ‎ ＝18（cm2）‎ ‎ 答：小胖画的梯形的面积是18平方厘米。‎ 附：课后作业设计 作业 说明 ‎1、完成书本p66的试一试（1）‎ ‎ 求出下列梯形的面积：（单位：cm）‎ ‎2、一个梯形的上底和下底的和是3.6分米，高是5分米。这个梯形的面积是多少平方分米？‎ ‎3、一个等腰梯形的周长是20厘米，一条腰长4厘米，高是7.5厘米。这个梯形的面积是多少平方厘米？‎ ‎4、一块直角梯形的土地，上底和下底分别是24米和44米，两条腰分别长15米和25米。这块梯形土地的面积是多少平方米？‎ ‎5、动手探究：‎ ‎1)能不能只用一个梯形，把它转化成一个平行四边形？‎ ‎（动手剪一剪、拼一拼，并画出草图，提示：上底、下底对折）‎ ‎2)思考：所拼成的平行四边形的面积又该怎样表示？‎ 基本训练：直接利用梯形的面积公式计算面积。‎ 变式训练：（层层递进）‎ 虽然没有具体告诉梯形的上底、下底的数据，但通过上底下底的和，计算梯形的面积。‎ 通过周长－腰长×2＝上底、下底的和的方法计算梯形的面积 通过找准直角梯形高（高比另一条腰短）的数据来计算梯形的面积。 ‎ 课后探究为下节课的学习作准备。并以此提高学生的动手操作能力和学习探究能力。‎ 总之，练习设计层层递进、形式多样、重点突出，既抓住了本节课的教学重点（理解并掌握梯形面积的计算方法），又发展了学生的的思维，培养了学生的动手实践能力。‎