2020-2021学年度第一学期广东省东莞市莞城区三校联考九年级第一次月考数学试卷（含答案）

2020-2021学年度第一学期广东省东莞市莞城区三校联考九年级第一次月考数学试卷（含答案）

‎2020-2021学年度第一学期广东省东莞市莞城区三校联考九年级第一次月考数学试卷（2020 09 30）‎ ‎（考试时间：90分钟 总分：120分）‎ 一、选择题（共10题；共30分）‎ ‎1.若关于x的方程ax2+3x+1＝0是一元二次方程，则a满足的条件是(   ) ‎ A. a≤ ‎9‎‎4‎                        B. a ‎>‎ 0                        C. a≠0                    D. a≤ ‎‎4‎‎9‎ ‎2.用配方法解方程x2﹣6x﹣4＝0，下列配方正确的是（  ） ‎ A. （x﹣3）2＝13           B. （x+3）2＝13          C. （x﹣6）2＝4              D. （x﹣3）2＝5‎ ‎3.若方程 x‎2‎‎-3x-k=0‎ 有实数根，则常数k的值可以是（    ） ‎ A. ‎-10‎                      B. ‎-5‎                         C. ‎-3‎                   D. ‎‎-1‎ ‎4.二次函数y＝2（x﹣3）2+2图象向左平移6个单位，再向下平移2个单位后，所得图象的函数表达式是（   ） ‎ A. y＝2x2﹣12x     B. y＝﹣2x2+6x+12     C. y＝2x2+12x+18      D. y＝﹣2x2﹣6x+18‎ ‎5.在同一坐标系中，二次函数 y=ax‎2‎+bx 与一次函数 y=ax-a 的图象可能是（    ） ‎ A.    B.      C.        D. ‎ ‎6.要组织一次排球邀请赛，参赛的每个队之间都要比赛一场，根据场地和时间等条件，赛程计划7天，每天安排4场比赛.设比赛组织者应邀请 x 个队参赛，则 x 满足的关系式为（   ） ‎ A. ‎1‎‎2‎x(x-1)=28‎      B. ‎1‎‎2‎x(x+1)=28‎          C. x(x-1)=28‎          D. ‎x(x+1)=28‎ ‎7.已知x1 ， x2是一元二次方程x2+x﹣3＝0的两个根，则x1+x2﹣x1x2的值为（　　） ‎ A. 1                      B. 2                    C. 3                               D. 4‎ ‎8.小明在研究抛物线 y=-‎(x-h)‎‎2‎-h+1‎ （ h 为常数）时，得到如下结论，其中正确的是（    ） ‎ A. 无论x取何实数，y的值都小于0 B. 该抛物线的顶点始终在直线 y=x-1‎ 上 C. 当 ‎-12h ，则 ‎y‎1‎‎>‎y‎2‎ ‎9.已知二次函数y＝ax2+bx+c自变量x与函数值y之间满足下列数量关系： ‎ x ‎2‎ ‎4‎ ‎5‎ y ‎0.38‎ ‎0.38‎ ‎6‎ ‎ ‎ 则（a+b+c）（ ‎-b+‎b‎2‎‎-4ac‎2a + ‎-b-‎b‎2‎‎-4ac‎2a ）值为（   ）‎ A. 24                        B. 36                       C. 6                          D. 4‎ ‎10.二次函数y＝ax2+bx+c（a≠0）的图象如图所示，c＜﹣1，其对称轴为直线x＝﹣1，与x轴的交点为（x1 ， 0）、（x2 ， 0），其中0＜x1＜1，有下列结论：①abc＞0；②﹣3＜x2＜﹣2；③4a﹣2b+c＜﹣1；④a﹣b＞am2+bm（m≠﹣1）；其中，正确的结论个数是（　　） ‎ A. 1个                   B. 2个                     C. 3个                      D. 4个 二、填空题（共7题；共28分）‎ ‎11.关于x的一元二次方程 ‎(k+2)x‎2‎+6x+k‎2‎+k-2=0‎ 有一个根是 ‎0‎ ，则k的值是________. ‎ ‎12.一元二次方程 ‎4x(x-2)=x-2‎ 的解为________． ‎ ‎13.某种植物的主干长出若干数目的支干，每个支干又长出同样数目的小分支，主干、支干和小分支的总数是21，则每个支干长出________． ‎ ‎14.如图，抛物线 y=ax‎2‎+1‎ 与 y 轴交于点 A ，过点 A 与 x 轴平行的直线交抛物线 y=4‎x‎2‎ 于点 B 、 C ，则线段 BC 的长为________.‎ ‎15.一个小球从水平面开始竖直向上发射，小球的高度h(m)关于运动时间t(s)的函数表达式为h=at2+bt，其图象如图所示．若小球在发射后第2s与第6s时的高度相等，则小球从发射到回到水平面共需时间________(s)。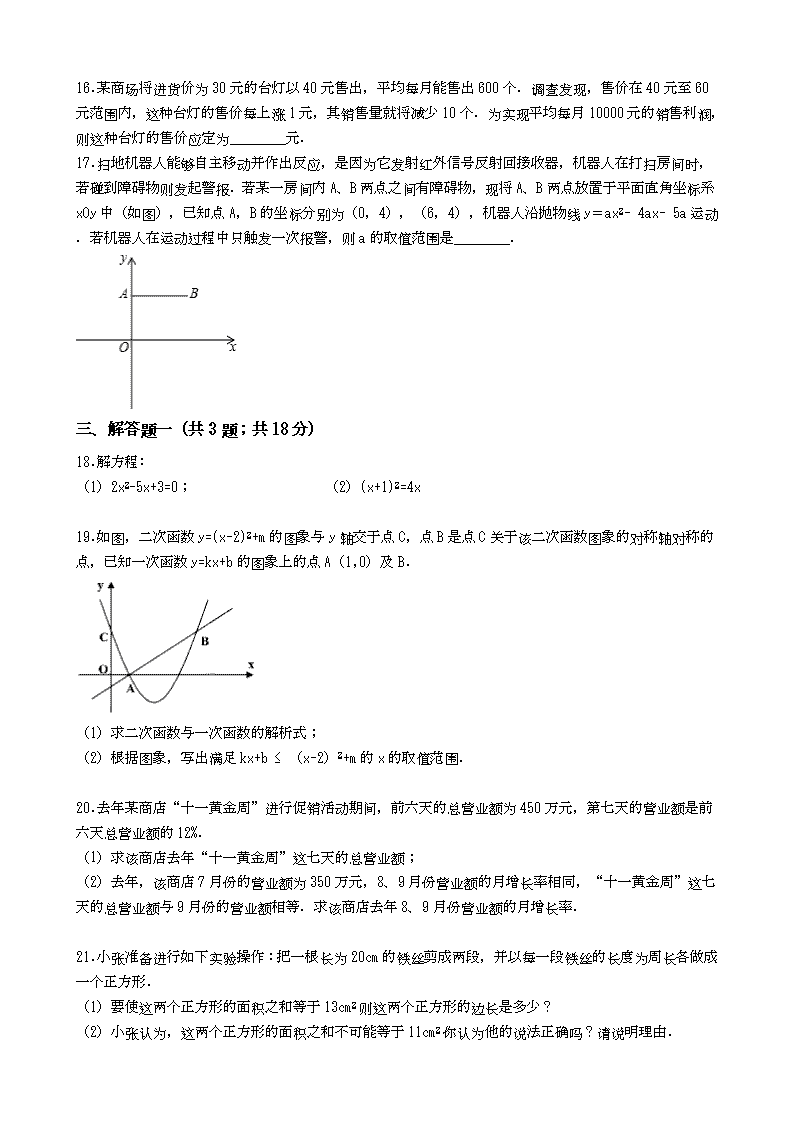 ‎ ‎ ‎ ‎16.某商场将进货价为30元的台灯以40元售出，平均每月能售出600个．调查发现，售价在40元至60元范围内，这种台灯的售价每上涨1元，其销售量就将减少10个．为实现平均每月10000元的销售利润，则这种台灯的售价应定为________元． ‎ ‎ ‎ ‎17.扫地机器人能够自主移动并作出反应，是因为它发射红外信号反射回接收器，机器人在打扫房间时，若碰到障碍物则发起警报．若某一房间内A、B两点之间有障碍物，现将A、B两点放置于平面直角坐标系xOy中（如图），已知点A，B的坐标分别为（0，4），（6，4），机器人沿抛物线y＝ax2﹣4ax﹣5a运动．若机器人在运动过程中只触发一次报警，则a的取值范围是________． ‎ 三、解答题一（共3题；共18分）‎ ‎18.解方程: ‎ ‎（1）2x2-5x+3=0； （2）(x+1)2=4x ‎ ‎19.如图，二次函数y=(x-2)2+m的图象与y轴交于点C，点B是点C关于该二次函数图象的对称轴对称的点，已知一次函数y=kx+b的图象上的点A（1,0）及B. （1）求二次函数与一次函数的解析式； （2）根据图象，写出满足kx+b‎≤‎（x-2）2+m的x的取值范围.‎ ‎20.去年某商店“十一黄金周”进行促销活动期间，前六天的总营业额为450万元，第七天的营业额是前六天总营业额的12%． ‎ ‎（1）求该商店去年“十一黄金周”这七天的总营业额； ‎ ‎（2）去年，该商店7月份的营业额为350万元，8、9月份营业额的月增长率相同，“十一黄金周”这七天的总营业额与9月份的营业额相等．求该商店去年8、9月份营业额的月增长率． ‎ ‎21.小张准备进行如下实验操作：把一根长为20cm的铁丝剪成两段，并以每一段铁丝的长度为周长各做成一个正方形. ‎ ‎（1）要使这两个正方形的面积之和等于13cm2则这两个正方形的边长是多少？ ‎ ‎（2）小张认为，这两个正方形的面积之和不可能等于11cm2你认为他的说法正确吗？请说明理由. ‎ ‎ ‎ 四、解答题二（共3题；共24分）‎ ‎22.已知关于 x 的一元二次方程 ‎(a+c)x‎2‎+2bx+c+(a-c)=0‎ ，其中 a 、 b 、 c 分别为 ‎△ABC 三边的长． ‎ ‎（1）如果 x=-1‎ 是方程的根，试判断 ‎△ABC 的形状，并说明理由； ‎ ‎（2）如果 ‎△ABC 是等边三角形，试求这个一元二次方程的根． ‎ ‎23.已知，在平面直角坐标系中，抛物线 y=x‎2‎-2mx+m‎2‎+2m-1‎ 的顶点为A，点B的坐标为 ‎(3,5)‎ ‎ ‎（1）求抛物线过点B时顶点A的坐标 ‎ ‎（2）点A的坐标记为 ‎(x,y)‎ ，求y与x的函数表达式； ‎ ‎（3）已知C点的坐标为 ‎(0,2)‎ ，当m取何值时，抛物线 y=x‎2‎-2mx+m‎2‎+2m-1‎ 与线段 BC 只有一个交点 ‎ 五、解答题（共2题；共20分）‎ ‎24.某游乐园有一个直径为16米的圆形喷水池，喷水池的周边有一圈喷水头，喷出的水柱为抛物线，在距水池中心3米处达到最高，高度为5米，且各方向喷出的水柱恰好在喷水池中心的装饰物处汇合．如图所示，以水平方向为x轴，喷水池中心为原点建立直角坐标系． ‎ ‎（1）求水柱所在抛物线（第一象限部分）的函数表达式； ‎ ‎（2）王师傅在喷水池内维修设备期间，喷水管意外喷水，为了不被淋湿，身高1.8米的王师傅站立时必须在离水池中心多少米以内？ ‎ ‎（3）经检修评估，游乐园决定对喷水设施做如下设计改进：在喷出水柱的形状不变的前提下，把水池的直径扩大到32米，各方向喷出的水柱仍在喷水池中心保留的原装饰物（高度不变）处汇合，请探究扩建改造后喷水池水柱的最大高度． ‎ ‎ ‎ ‎25.二次函数 y=ax‎2‎+bx+3‎ 的图象与x轴交于A(2，0)，B(6，0)两点，与y轴交于点C，顶点为E. ‎ ‎（1）求这个二次函数的表达式，并写出点E的坐标； ‎ ‎（2）如图①，D是该二次函数图象的对称轴上一个动点，当BD的垂直平分线恰好经过点C时，求点D的坐标； ‎ ‎（3）如图②，P是该二次函数图象上的一个动点，连接OP，取OP中点Q，连接QC，QE，CE，当△CEQ的面积为12时，求点P的坐标. ‎ ‎ ‎ 答案 一、选择题 ‎1.解：∵ 关于x的方程ax2+3x+1＝0是一元二次方程，根据一元二次方程的定义可得：a≠0. ‎ 故答案为：C ‎2.解：方程x2﹣6x﹣4＝0变形得：x2﹣6x＝4， ‎ 配方得：x2﹣6x+9＝13，即（x﹣3）2＝13.‎ 故答案为：A.‎ ‎3.解：∵关于x的方程 x‎2‎‎-3x-k=0‎ 有实数根， ‎ ‎∴△≥0，即（－3）2＋4k≥0，解得 k≥-‎‎9‎‎4‎ ，‎ ‎∴k的值可以是 ‎-1‎ ，‎ 故答案为：D ． ‎ ‎4.解： 二次函数y＝2（x﹣3）2+2图象向左平移6个单位，再向下平移2个单位后，所得图象的函数表达式是y＝2（x﹣3+6）2+2-2，即y＝2x2+12x+18. 故答案为：C. 5.由一次函数 y=ax-a 可知，一次函数的图象与x轴交于点（1，0），即可排除B、C、D， ‎ 对于A选项，‎ 观察二次函数 y=ax‎2‎+bx 的图象，‎ ‎∵开口向上，‎ ‎∴ a>0‎ ，‎ 当 a>0‎ 时，一次函数 y=ax-a 经过一、二、四象限，‎ ‎∴A选项符合题意，‎ 故答案为：A．‎ ‎6.解：由题可得： ‎1‎‎2‎x(x-1)=4×7‎ ‎ 即： ‎‎1‎‎2‎x(x-1)=28‎ 故答案是：A.‎ ‎7.解：∵x1 ， x2是一元二次方程x2+x﹣3＝0的两个根， ‎ ‎∴x1+x2＝﹣1，x1x2＝﹣3，‎ 则原式＝﹣1﹣（﹣3）＝﹣1+3＝2.‎ 故答案为：B.‎ ‎8.解：A、由函数表达式的性质可得，抛物线的顶点坐标为（h，-h+1），抛物线的最大值为-h+1，若h<1，则y>0，故A项不符合题意； ‎ B、由题可得出抛物线的顶点坐标为（h，-h+1），‎ 当x=h时，代入y=x-1得 y=h-1≠1-h ，故B项不符合题意；‎ C、由题意得，抛物线在x=h左侧时，y随x的增大而增大，‎ ‎∴ h≥2‎ ，故C项不符合题意；‎ ‎ ‎ D、∵x12h，‎ ‎∴x1在x=h左侧且更靠近x=h，‎ ‎∵在 y=-‎(x-h)‎‎2‎-h+1‎ 中，x离x=h越近，y值越大，‎ ‎∴y1>y2 ， 故D项符合题意；‎ 故答案为：D．‎ ‎9.由表格数据可知抛物线的对称轴为x＝﹣ b‎2a ＝ ‎2+4‎‎2‎ ＝3， ‎ ‎∴﹣ ba ＝6，‎ ‎∴x＝1与x＝5时的函数值相等，‎ ‎∴x＝1时，y＝6，即a+b+c＝6，‎ ‎∴（a+b+c）（ ‎-b+b‎2‎-4ac‎2a‎+‎‎-b-b‎2‎-4ac‎2a ）＝6×（﹣ ba ）＝6×6＝36．‎ 故答案为：B ． ‎ ‎10. ‎∵‎ 抛物线开口向上 ‎‎∴a>0‎ ‎∵‎‎ 对称轴为 ‎x=-b‎2a=-1‎ ‎∴‎‎ a、b同号，则 b>0‎ ‎‎∵c<-1‎ ‎∴abc<0‎‎ ，则①错误 ‎∵‎‎ 对称轴为 x=-1‎ ，与x轴的交点为 ‎‎(x‎1‎,0),(x‎2‎,0)‎ ‎∴x‎1‎‎+‎x‎2‎‎2‎=-1‎‎ ，即 ‎x‎1‎‎=-2-‎x‎2‎ ‎∵0

查看更多