中考数学专题复习练习:综合函数考点探究
函数考点探究:六、综合探究
考点18:利用函数的图象解决问题
1、利用图象求一次函数的解析式
y
x
2
3
o
例43.如图,直线AB与x轴、y轴分别交于A、B两点,
(1)写出A、B两点的坐标;
(2)求直线AB的函数解析式。
x
y
o
-4
2、利用图象确定变量的取值范围
例44.如图,直线y=kx+b与x轴交于(-4,0),
则当y>0时,x的取值为( )
x
y
o
-2
1
A.x>-4 B.x>0 C.x<-4 D.x<0
例45.已知一次函数y=kx+b的图象如图所示,
则当x<0时,y的取值范围是( )
A.y>0 B.y<0 C.-2
0的解为 。
4、利用特殊值化简或进行相应判断
x
y
o
1
-1
例47.已知一次函数y=ax+b的图象如图所示,
则下列说法中正确的有( )个。
(1)a<0,b<0; (2)a+b>0;
(3)a-b>0; (4)|a+b|-|a-b|=-2b
A.1 B.2 C.3 D.4
(本题利用特殊值:x=1时,y=a+b;x=-1时,y=b-a进行判断)
5、利用图象求几何图形的面积
在平面直角坐标系中求△的面积,关键在于以在坐标轴上的一边为底,再
利用△的面积公式求解;
若所求△没有一边在坐标轴上时,则要利用有边在坐标轴上的△来转换。
(同量也涉及到点坐标的求法和点到坐标轴的距离)
例48.如图,一次函数y=x+5的图像交x轴于点B,交正比例函数的图像于点A,
且点A的横坐标为-4,
(1)求正比例函数的解析式.
(2)求△AOB的面积。
例49.已知直线y=-x+5与x轴交于点A,直线上有一点p,满足△POA的面积为
10,求点p的坐标。
考点19:利用函数知识解决生活中的实际问题
1、“分段性”问题
这种问题在变化过程中,规律是动态的,在解决时应按以下步骤:
(1)把具有相同变化规律的自变量取值范围看作一段,先分段建立函数关系式;
(2)然后按要求分段进行处理。
例50.某自来水公司为鼓励居民节约用水,每月按用水量分段收费的方法,若某户居
民应交水费y(元)与用水量x(吨)的函数关系如图所示。
(1)分别写出当0≤x≤15和x≥15时,y与x的函数关系式;
(2)若某用户该月用水21吨,则应交水费多少元?
y
x
o
39.5
27
15
20
例51.某市计程车收费标准如下:前5公里起步价为8元,超出5公里每公里多收费1.6元(不足1公里按1公里计算)。
(1)写出收费y(元)与行程x(公里)之间的函数关系式;
(2)分别求出行程为4公里、13公里的收费情况。
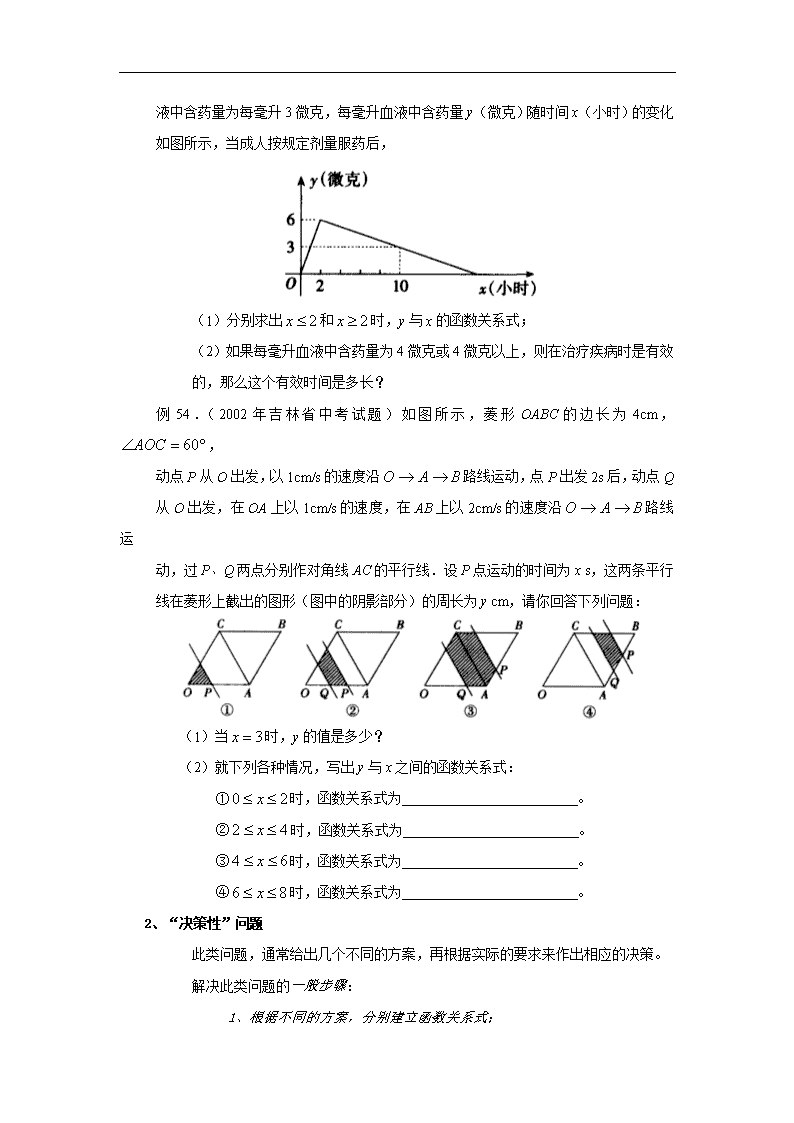
例53.某医药研究所开发一种新药,在试验药效时发现,如果成人按规定剂量服用,
那么服药2小时后血液中含药量最高,达每毫升6微克,接着逐步衰减,10小时后血
液中含药量为每毫升3微克,每毫升血液中含药量y(微克)随时间x(小时)的变化
如图所示,当成人按规定剂量服药后,
(1)分别求出和时,y与x的函数关系式;
(2)如果每毫升血液中含药量为4微克或4微克以上,则在治疗疾病时是有效
的,那么这个有效时间是多长?
例54.(2002年吉林省中考试题)如图所示,菱形OABC的边长为4cm,,
动点P从O出发,以1cm/s的速度沿路线运动,点P出发2s后,动点Q
从O出发,在OA上以1cm/s的速度,在AB上以2cm/s的速度沿路线运
动,过P、Q两点分别作对角线AC的平行线.设P点运动的时间为x s,这两条平行
线在菱形上截出的图形(图中的阴影部分)的周长为y cm,请你回答下列问题:
(1)当时,y的值是多少?
(2)就下列各种情况,写出y与x之间的函数关系式:
①时,函数关系式为 。
②时,函数关系式为 。
③时,函数关系式为 。
④时,函数关系式为 。
2、“决策性”问题
此类问题,通常给出几个不同的方案,再根据实际的要求来作出相应的决策。
解决此类问题的一般步骤:
1、根据不同的方案,分别建立函数关系式;
2、在实际要求中,分别计算出函数值;
3、通过比较函数值的大小,确定相应的策略。
例55.(2002年哈尔滨市中考试题)哈尔滨市移动通讯公司开设了两种通讯业务:“全
球通”使用者先缴50元月基础费,然后每通话1min,再付电话费0.4元;“神州行”
不缴月基础费,每通话1min,付话费0.6元(这里均指市内通话).若一个月内通话
x min,两种通讯方式的费用分别为和元.
(1)写出与x之间的函数关系式;
(2)一个月内通话多少分钟,两种通讯方式的费用相同?
(3)若某人预计一个月内使用话费200元,则应选择哪种通讯方式较合算?
例56.(2003年贵阳市中考试题)某校准备在甲、乙两家公司为毕业班学生制作一批
纪念册.甲公司提出:每册收材料费5元,另收设计费1500元;乙公司提出:每册
收材料费8元,不收设计费.
(1)请写出制作纪念册的册数x与甲公司的收费(元)的函数关系式;
(2)请写出制作纪念册数x与乙公司的收费(元)的函数关系式;
(3)如果学校派你去甲、乙两家公司订做纪念册,你会选择哪家公司?
3、“规律性”问题
某一量随另一量的变化而呈规律性变化的问题。利用函数思想是解决这类问
题的一般步骤:
1、列表;2、猜想(函数关系式);
3、得到规律;4、验证规律;
5、运用规律解决问题。
例57.用黑白两种颜色的正六边形地面砖按如下的规律拼成若干个图案:
(1) (2) (3)
问(1)第4个图案中有白色地砖 块;
(2)第n个图案中有白色地砖 块。
4、“最值性”问题
就是利用在实际问题中自变量受到的限制(可能出现最大值或最小值),来
解决诸如“成本最低”、“利润最大”、“费用最少”的问题。一般步骤:
1、列出函数解析式;
2、根据实际问题,求出自变量的取值范围;
3、根据函数的性质(一次函数的性质由k决定),在自变量的取值范围中,确
定函数的最值。
例58.某饮料厂为了开发新产品,用A、B两种
果汁原料各19千克、17.2千克,试制甲、乙两
种新型饮料50千克,右表是相关的数据:
(1)设甲种饮料配制x千克,试求x的取值范围;
(2)若甲、乙两种饮料每千克的成本分别为4元、3元,设两种饮料的总成
本为y元,请写出y与x之间的函数关系式;并确定当甲配制多少千克时,成本总额最少。