人教版九年级数学上册专题训练(十二)与圆的切线有关的计算与证明

人教版九年级数学上册专题训练(十二)与圆的切线有关的计算与证明

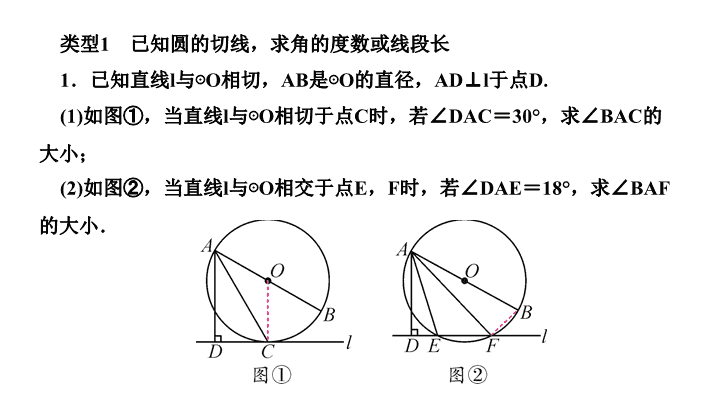
第二十四章　圆 人教版 专题训练(十二)　与圆的切线有关的计算与证明 类型 1 　已知圆的切线，求角的度数或线段长 1 ．已知直线 l 与⊙ O 相切， AB 是⊙ O 的直径， AD⊥l 于点 D. (1) 如图①，当直线 l 与⊙ O 相切于点 C 时，若∠ DAC ＝ 30° ，求∠ BAC 的大小； (2) 如图②，当直线 l 与⊙ O 相交于点 E ， F 时，若∠ DAE ＝ 18° ，求∠ BAF 的大小． 2 ． ( 玉林中考 ) 如图，在△ ABC 中， AB ＝ AC ＝ 5 ， BC ＝ 6 ，以 AB 为直径作⊙ O 分别交于 AC ， BC 于点 D ， E ，过点 E 作⊙ O 的切线 EF 交 AC 于点 F ，连接 BD. (1) 求证： EF 是△ CDB 的中位线； (2) 求 EF 的长． 类型 2 　三角形或四边形的内切圆问题 3 ．如图，在△ ABC 中， AB ＝ AC ，⊙ O 是△ ABC 的内切圆，它与 AB ， BC ， CA 分别相切于点 D 、 E 、 F. (1) 求证： BE ＝ CE ； (2) 若∠ A ＝ 90° ， AB ＝ AC ＝ 2 ，求⊙ O 的半径． 4 ．如图，⊙ O 是四边形 ABCD 的内切圆，切点为 E ， F ， G ， H ，已知 AD∥BC ， AB ＝ CD ， DO ＝ 6 cm ， CO ＝ 8 cm. (1) 求证： AB ＋ CD ＝ AD ＋ BC ； (2) 求四边形 ABCD 的周长． 类型 3 　先证圆的切线，再解决问题 5 ．如图， AB ＝ BC ，以 AB 为直径的⊙ O 交 AC 于点 D ，过点 D 作 DE⊥BC ，垂足为 E. (1) 求证： DE 是⊙ O 的切线； (2) 作 DG⊥AB 交⊙ O 于点 G ，垂足为 F ，若∠ A ＝ 30° ， AB ＝ 8 ，求弦 DG 的长． 6 ． ( 天水中考 ) 如图， AB ， AC 分别是⊙ O 的直径和弦， OD⊥AC 于点 D. 过点 A 作⊙ O 的切线与 OD 的延长线交于点 P ， PC ， AB 的延长线交于点 F. (1) 求证： PC 是⊙ O 的切线； (2) 若∠ ABC ＝ 60° ， AB ＝ 10 ，求线段 CF 的长． 类型 4 　平面直角坐标系与圆的切线综合 7 ．如图，在平面直角坐标系中，⊙ O 是以原点 O 为圆心，半径为 2 的圆， P 是在第一象限内的⊙ O 上一动点，过点 P 作⊙ O 的切线分别与 x ， y 轴相交于点 A 、 B. (1) 当点 P 为 AB 中点时，请直接写出 P 点坐标； (2) 点 P 在运动时，线段 AB 的长度也在发生变化，请求线段 AB 的最小值，并说明理由； (3) 在⊙ O 上是否存在一点 Q ，使得以 Q ， O ， A ， P 为顶点的四边形是平行四边形？若存在，请求出 Q 点的坐标；若不存在，请说明理由． (2) 线段 AB 长度的最小值为 4 ，理由如下：如图②，连接 OP ，∵ AB 切⊙ O 于点 P ，∴ OP⊥AB ，取 AB 的中点 C ， 则 AB ＝ 2OC ；当 OC ＝ OP 时， OC 最短，即 AB 最短，此时 AB ＝ 4