2019年安徽省合肥市长丰县中考二模数学试卷

2019年安徽省合肥市长丰县中考二模数学试卷

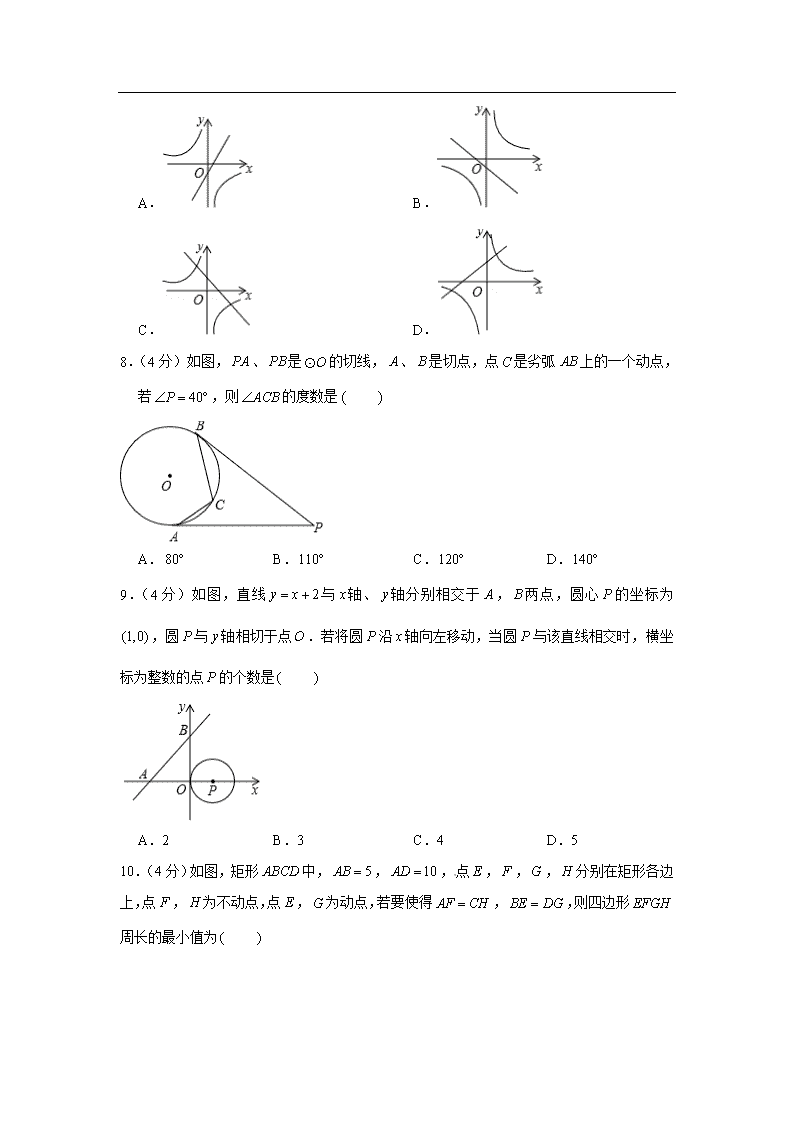
‎2019年安徽省合肥市长丰县中考数学二模试卷 一、选择题（本大题共10小题，每小题4分，满分40分）‎ ‎1．（4分）4的相反数是　　‎ A．4 B． C． D．‎ ‎2．（4分）2018年国庆假日第二天安徽省黄山风景区接待游客2.96万人次，同比下降，门票收人479.87万元万元用科学记数法表示为　　‎ A．元 B．元 ‎ C．元 D．元 ‎3．（4分）下列计算正确的是　　‎ A． B． C． D．‎ ‎4．（4分）下面几何体中，其主视图与俯视图相同的是　　‎ A． B． C． D．‎ ‎5．（4分）不等式组的解集是　　‎ A． B． C． D．‎ ‎6．（4分）如图，已知直线，，，则的度数是　　‎ A． B． C． D．‎ ‎7．（4分）在同一平面直角坐标系中，函数与的图象可能是　　‎ A． B． ‎ C． D．‎ ‎8．（4分）如图，、是的切线，、是切点，点是劣弧上的一个动点，若，则的度数是　　‎ A． B． C． D．‎ ‎9．（4分）如图，直线与轴、轴分别相交于，两点，圆心的坐标为，圆与轴相切于点．若将圆沿轴向左移动，当圆与该直线相交时，横坐标为整数的点的个数是　　‎ A．2 B．3 C．4 D．5‎ ‎10．（4分）如图，矩形中，，，点，，，分别在矩形各边上，点，为不动点，点，为动点，若要使得，，则四边形周长的最小值为　　‎ A． B． C． D．‎ 二、填空题（本大题共4小题，每小题5分，满分20分）‎ ‎11．（5分）因式分解：　　．‎ ‎12．（5分）如图，菱形的三个顶点在二次函数的图象上，点，分别是该抛物线的顶点和抛物线与轴的交点，则点的坐标为　　．‎ ‎[来源:学科网ZXXK]‎ ‎13．（5分）已知关于的一元二次方程有两个不相等的实数根，则的取值范围是　 　．‎ ‎14．（5分）如图，矩形中，，．点为射线上的一个动点，将沿着折叠，当△为直角三角形时，的长为　　．‎ 三、（本大题共2小题，每小题8分，满分16分）‎ ‎15．（8分）计算：．‎ ‎16．（8分）两位数相乘：，，，，‎ ‎（1‎ ‎）认真观察、分析：以上各式中的因数的十位数与个位数有何关系，因数与积之间有何规律，请用字母将规律表示出来；‎ ‎（2）验证你得到的规律．‎ 四、（本大题共2小题，每小题8分，满分16分）‎ ‎17．（8分）已知如图，四边形是正方形，点是边上任意一点，，且交正方形外角平分线于点，求证：．‎ ‎18．（8分）“有求胜的这种心态很好，但是不可能常胜，也不可能全胜，一个人能力毕竞是有限的，希望你们能集中自己的特长，在某一方面去集中发展．”在习近平总书记视察学校时的讲话启发下，今年，我市某学校开展了“跳绳大课间“活动，现需要购进100个某品牌的跳绳供学生使用．经调查，该品牌跳绳2017年单价为25元，2019年单价为36元．‎ ‎（1）求2017年到2019年该品牌跳绳单价平均每年增长的百分率；‎ ‎（2）选购期间发现该品牌跳绳在两个文体用品商场有不同的促销方案：甲商场买十送一，乙商场全场九折，试问去哪个商场购买更优惠？‎ 五、（本大题共2小题，每小题10分，满分20分）‎ ‎19．（10分）如图，在中，，，，，求的长．（最后结果精确到，参考数据：，，，，‎ ‎20．（10分）如图，是的外接圆，，，连接并延长至点，使，交于点．‎ ‎（1）求证：是的切线；‎ ‎（2）求的长．‎ 六、（本题满分12分）‎ ‎21．（12分）我市某水果经销商为了解市民对销量较好的梨子、橘子、香蕉、苹果（以下分别用、、、表示）这四种水果的喜爱情况，对某居民区市民进行了抽样调查，并将调查情况绘制成如下两幅统计图（尚不完整）‎ 请根据以上信息回答：‎ ‎（1）本次参加抽样调查的市民有多少人？‎ ‎（2）将两幅不完整的图补充完整；‎ ‎（3）若居民区有8000人，请估计爱吃苹果的人数；‎ ‎（4）若取、、、各一个，分别放在四个形状相同且不透明的盒子里，小王吃了两个，用列表或画树状图的方法，求他第二个吃到的恰好是的概率 七、（本题满分12分）‎ ‎22．（12分）某公司销售一种产品，产品成本为40元千克，经市场调查，若按50元千克销售，每月可销售，销售单价每上涨2元，月销售量就减少 ‎（1）写出月销售利润（单位：元）与销售单价（单位：元千克）之间的函数解析式（不要求写出的取值范围）；‎ ‎（2）当销售单价定为60元时，计算月销售量和月销售利润；‎ ‎（3）当销售单价定为多少元时能获得最大利润？最大利润是多少？‎ 八、（本题满分14分）‎ ‎23．（14分）如图①，在矩形中，点是边上的一点，连接交于点．‎ ‎（1）若，点是边的中点，求的值；[来源:学科网ZXXK]‎ ‎（2）如图②，若，点是边的三等分点，求的值；‎ ‎（3）如图③，若点是边的中点，，求的值．‎ ‎2019年安徽省合肥市长丰县中考数学二模试卷 参考答案与试题解析 一、选择题（本大题共10小题，每小题4分，满分40分）‎ ‎1．（4分）4的相反数是　　‎ A．4 B． C． D．‎ ‎【解答】解：根据概念，的相反数）（4），则4的相反数是．‎ 故选：．‎ ‎2．（4分）2018年国庆假日第二天安徽省黄山风景区接待游客2.96万人次，同比下降，门票收人479.87万元万元用科学记数法表示为　　‎ A．元 B．元 ‎ C．元 D．元 ‎【解答】解：将479.87万用科学记数法表示为：．‎ 故选：．‎ ‎3．（4分）下列计算正确的是　　‎ A． B． C． D．‎ ‎【解答】解：．，此选项错误；‎ ‎．，此选项正确；‎ ‎．，此选项错误；‎ ‎．，此选项错误；‎ 故选：．‎ ‎4．（4分）下面几何体中，其主视图与俯视图相同的是　　‎ A． B． C． D．‎ ‎【解答】解：、圆柱主视图是矩形，俯视图是圆；‎ ‎、圆锥主视图是三角形，俯视图是圆；‎ ‎、正方体的主视图与俯视图都是正方形；‎ ‎、三棱柱的主视图是矩形与俯视图都是三角形；‎ 故选：．‎ ‎5．（4分）不等式组的解集是　　‎ A． B． C． D．‎ ‎【解答】解：解不等式，得：，‎ 解不等式，得：，‎ 则不等式组的解集为，‎ 故选：．‎ ‎6．（4分）如图，已知直线，，，则的度数是　　‎ A． B． C． D．‎ ‎【解答】解：如图，，‎ ‎，‎ ‎．，‎ ‎，‎ 故选：．‎ ‎7．（4分）在同一平面直角坐标系中，函数与的图象可能是　　‎ A． B． ‎ C． D．‎ ‎【解答】解：、由反比例函数图象得，则一次函数图象经过第二、三、四象限，所以选项错误；‎ ‎、由反比例函数图象得，则一次函数图象经过第一、二、三象限，所以选项错误；‎ ‎、由反比例函数图象得，则一次函数图象经过第二、三、四象限，所以选项错误；‎ ‎、由反比例函数图象得，则一次函数图象经过第一、二、三象限，所以选项正确．‎ 故选：．‎ ‎8．（4分）如图，、是的切线，、是切点，点是劣弧上的一个动点，若，则的度数是　　‎ A． B． C． D．‎ ‎【解答】解：连接，，在优弧上任取一点（不与、重合），‎ 连接，，如图所示：‎ ‎、是的切线，‎ ‎，，‎ ‎，又，‎ ‎，‎ 圆周角与圆心角都对弧，‎ ‎，‎ 又四边形为圆内接四边形，‎ ‎，‎ 则．‎ 故选：．‎ ‎9．（4分）如图，直线与轴、轴分别相交于，两点，圆心的坐标为，圆与轴相切于点．若将圆沿轴向左移动，当圆与该直线相交时，横坐标为整数的点的个数是　　‎ A．2 B．3 C．4 D．5‎ ‎【解答】解：直线与轴、轴分别相交于，两点，‎ 圆心的坐标为，‎ 点的坐标为：，‎ 点的坐标为：，‎ ‎，‎ 将圆沿轴向左移动，当圆与该直线相切于时，，‎ 根据△，‎ ‎，‎ ‎，‎ 的坐标为：，‎ 将圆沿轴向左移动，当圆与该直线相切于时，，‎ 根据△，‎ ‎，‎ ‎，‎ 的坐标为：，，‎ 从到，整数点有，，故横坐标为整数的点的个数是2个．‎ 故选：．‎ ‎10．（4分）如图，矩形中，，，点，，，分别在矩形各边上，点，为不动点，点，为动点，若要使得，，则四边形周长的最小值为　　‎ A． B． C． D．‎ ‎【解答】解：作点关于的对称点，连接交于点，此时四边形周长取最小值，过点作于点，如图所示．‎ ‎，，‎ ‎，‎ ‎，‎ ‎，‎ ‎．‎ 故选：．‎ 二、填空题（本大题共4小题，每小题5分，满分20分）‎ ‎11．（5分）因式分解：　　．‎ ‎【解答】解：‎ ‎．‎ 故答案为：．‎ ‎12．（5分）如图，菱形的三个顶点在二次函数的图象上，点，分别是该抛物线的顶点和抛物线与轴的交点，则点的坐标为　　．‎ ‎【解答】解：的对称轴是，与轴的交点坐标是，‎ 点的坐标是，‎ 菱形的三个顶点在二次函数的图象上，‎ 点、分别是该抛物线的顶点和抛物线与轴的交点，‎ 点与点关于直线对称，‎ 点的坐标为．‎ 故答案为：．‎ ‎13．（5分）已知关于的一元二次方程有两个不相等的实数根，则的取值范围是　，且　．‎ ‎【解答】解：关于的一元二次方程有两个不相等的实数根，‎ ‎△，即，‎ 解这个不等式得，，‎ 又二次项系数是，‎ ‎．‎ 故的取值范围是且．‎ ‎14．（5分）如图，矩形中，，．点为射线上的一个动点，将沿着折叠，当△为直角三角形时，的长为　3或27　．‎ ‎【解答】解：分两种情况：‎ ‎①当点在线段上时，如图1所示，，‎ 在△中，．‎ ‎，‎ ‎、、三点共线．‎ 设，则，，‎ 在中，利用勾股定理可得 ‎，[来源:Zxxk.Com]‎ 解得，即；‎ ‎②当点在延长线上时，如图2所示，，‎ 根据折叠的对称性可知，‎ ‎、、三点共线．‎ 在△中，．[来源:Zxxk.Com]‎ 设，则，，‎ 在中，利用勾股定理可得 ‎，‎ 解得，即，‎ 故答案为3或27．‎ 三、（本大题共2小题，每小题8分，满分16分）‎ ‎15．（8分）计算：．‎ ‎【解答】解：原式．‎ ‎16．（8分）两位数相乘：，，，，‎ ‎（1）认真观察、分析：以上各式中的因数的十位数与个位数有何关系，因数与积之间有何规律，请用字母将规律表示出来；‎ ‎（2）验证你得到的规律．‎ ‎【解答】解：（1）上述等式的规律是：两因数的十位数相等，个位数相加等于10，而积后两位是两因数个位数相乘、前两位是十位数乘以（十位数；‎ 如果用表示十位数，表示个位数，‎ 则第一个因数为，第二个因数为，积为；‎ 表示出来为：；‎ ‎（2）左边 右边 ‎ 成立．‎ 四、（本大题共2小题，每小题8分，满分16分）‎ ‎17．（8分）已知如图，四边形是正方形，点是边上任意一点，，且交正方形外角平分线于点，求证：．‎ ‎【解答】证明：在上截取，连接，‎ ‎，‎ ‎，‎ ‎，‎ ‎，，‎ ‎，‎ 在和中，‎ ‎，‎ ‎．‎ ‎18．（8分）“有求胜的这种心态很好，但是不可能常胜，也不可能全胜，一个人能力毕竞是有限的，希望你们能集中自己的特长，在某一方面去集中发展．”在习近平总书记视察学校时的讲话启发下，今年，我市某学校开展了“跳绳大课间“活动，现需要购进100个某品牌的跳绳供学生使用．经调查，该品牌跳绳2017年单价为25元，2019年单价为36元．‎ ‎（1）求2017年到2019年该品牌跳绳单价平均每年增长的百分率；‎ ‎（2）选购期间发现该品牌跳绳在两个文体用品商场有不同的促销方案：甲商场买十送一，乙商场全场九折，试问去哪个商场购买更优惠？‎ ‎【解答】解：（1）设2017年到2019年该品牌跳绳单价平均每年增长的百分率为，‎ 依题意，得：，‎ 解得：，（舍去）．‎ 答：2017年到2019年该品牌跳绳单价平均每年增长的百分率为．‎ ‎（2）（根，‎ 在甲商场需购买91根．‎ 在甲商场购买所需费用为（元，‎ 在乙商场购买所需费用为（元，‎ ‎．‎ 答：去乙商场购买更优惠．‎ 五、（本大题共2小题，每小题10分，满分20分）‎ ‎19．（10分）如图，在中，，，，，求的长．（最后结果精确到，参考数据：，，，，‎ ‎【解答】解：，，，‎ ‎，，，‎ 是等腰三角形，，‎ 在中，，‎ ‎，‎ ‎，‎ ‎；‎ ‎20．（10分）如图，是的外接圆，，，连接并延长至点，使，交于点．‎ ‎（1）求证：是的切线；‎ ‎（2）求的长．‎ ‎【解答】解：（1）连接、，‎ ‎，‎ ‎，‎ 为直径，‎ ‎，‎ ‎，‎ ‎，，‎ ‎，，‎ ‎，‎ ‎，‎ 即，‎ 为半径，‎ 是的切线．‎ ‎（2），‎ ‎．‎ ‎，‎ ‎，即，‎ ‎，‎ ‎．‎ 在中，，‎ ‎，，‎ ‎，即．‎ 六、（本题满分12分）‎ ‎21．（12分）我市某水果经销商为了解市民对销量较好的梨子、橘子、香蕉、苹果（以下分别用、、、表示）这四种水果的喜爱情况，对某居民区市民进行了抽样调查，并将调查情况绘制成如下两幅统计图（尚不完整）‎ 请根据以上信息回答：‎ ‎（1）本次参加抽样调查的市民有多少人？‎ ‎（2）将两幅不完整的图补充完整；‎ ‎（3）若居民区有8000人，请估计爱吃苹果的人数；‎ ‎（4）若取、、、各一个，分别放在四个形状相同且不透明的盒子里，小王吃了两个，用列表或画树状图的方法，求他第二个吃到的恰好是的概率 ‎【解答】解：（1）本次参加抽样调查的市民总人数为（人；‎ ‎（2）类的人数是：（人，‎ 类所占的百分比是：，‎ 类所占的百分比是：．‎ ‎（3）估计爱吃苹果的人数为（人；‎ ‎（4）如图，‎ 得到所有等可能的情况有12种，他第二个吃到的恰好是的有3种结果，‎ 所以他第二个吃到的恰好是的概率为．‎ 七、（本题满分12分）‎ ‎22．（12分）某公司销售一种产品，产品成本为40元千克，经市场调查，若按50元千克销售，每月可销售，销售单价每上涨2元，月销售量就减少 ‎（1）写出月销售利润（单位：元）与销售单价（单位：元千克）之间的函数解析式（不要求写出的取值范围）；‎ ‎（2）当销售单价定为60元时，计算月销售量和月销售利润；‎ ‎（3）当销售单价定为多少元时能获得最大利润？最大利润是多少？‎ ‎【解答】解：（1）由题意得：，‎ 即月销售利润（单位：元）与销售单价（单位：元千克）之间的函数解析式为：‎ ‎．‎ ‎（2）当元，月销量为，[来源:学科网]‎ 将代入，解得，‎ 故月销售利润为8000元．‎ ‎（3），‎ 当时，．‎ 故当销售单价定位70元时可获得最大利润，最大利润为9000元．‎ 八、（本题满分14分）‎ ‎23．（14分）如图①，在矩形中，点是边上的一点，连接交于点．‎ ‎（1）若，点是边的中点，求的值；‎ ‎（2）如图②，若，点是边的三等分点，求的值；‎ ‎（3）如图③，若点是边的中点，，求的值．‎ ‎【解答】解：（1）如图①，作交于点，则，‎ ‎，‎ ‎，‎ ‎，‎ 点是的中点，‎ ‎，‎ ‎，‎ ‎；‎ ‎（2）如图②，作交于，则，‎ ‎，‎ ‎，‎ ‎，‎ 点是的三等分点，‎ ‎，‎ ‎，‎ ‎；‎ ‎（3）如图③，作交于，则，‎ ‎，‎ ‎，‎ ‎，‎ 点是的中点，‎ ‎，‎ ‎，‎ ‎．‎ 声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布 日期：2019/6/6 17:25:09；用户：老王；邮箱：41608708@qq.com；学号：1007195‎