江西专版2020中考数学复习方案第三单元函数第10课时一次函数课件

江西专版2020中考数学复习方案第三单元函数第10课时一次函数课件

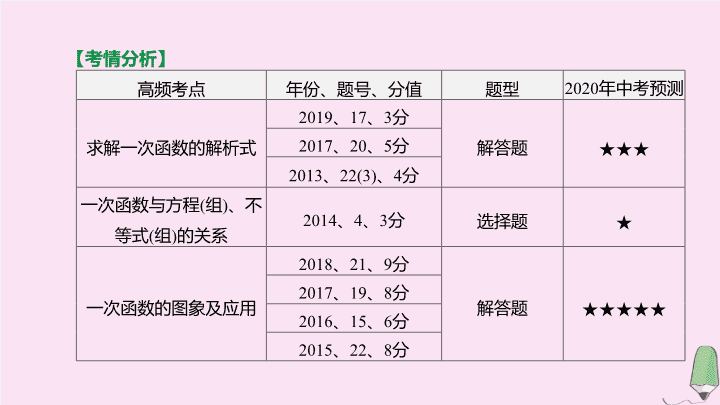
第 10 课时 一次函数 第三单元　函数 【 考情分析 】 高频考点 年份、题号、分值 题型 2020 年中考预测 求解一次函数 的解析 式 2019 、 17 、 3 分 解答题 ★★★ 2017 、 20 、 5 分 2013 、 22(3) 、 4 分 一次函数与方程 ( 组 ) 、不等式 ( 组 ) 的关系 2014 、 4 、 3 分 选择题 ★ 一次函数 的图象 及应用 2018 、 21 、 9 分 解答题 ★★★★★ 2017 、 19 、 8 分 2016 、 15 、 6 分 2015 、 22 、 8 分 1 . 一般地 , 形如 y=kx ( k 是常数 , k ≠0) 的函数 , 叫做正比例函数 , 其中 k 叫做比例系数 . 考点一　一次函数的概念 考点聚焦 2 . 一般地 , 形如 y=kx + b ( k , b 是常数 , k ≠0) 的函数 , 叫做一次函数 . 当 b= 0 时 , y=kx + b 即 y=kx , 所以说正比例函数是一种特殊的一次函数 . 考点二　一次函数的图象与性质 k> 0 k< 0 图象 经过的 象限 b> 0 b= 0 b< 0 b> 0 b= 0 b< 0 一、二、 三 一、三 ①   ②   ③   二、三、 四 一、三、四 一、二、四 二、四 （续表） 增大 减小 b 考点三　一次函数的解析式的确定 1 . 方法 : 待定系数法 2 . 步骤 : (1) 设 : 设一般式 y=kx + b ( k ≠0); (2) 列 : 找出直线上两点的坐标 , 分别代入 y=kx + b , 得到关于 k , b 的方程组 ; (3) 解 : 解方程组 , 求得 k , b 的值 ; (4) 依据 k , b 的值 , 写出一次函数的解析式 . 考点四　一次函数与一次方程 ( 组 ) 、一元一次不等式的关系 x 0 图 1 0 -1 2 . 一次函数与不等式的关系 (1) 不等式 kx + b> 0( kx + b< 0) 的解集 ⇔ 函数 y=kx + b ( k ≠0) 的图象在 x 轴上方 ( 下方 ) 的部分对应的 x 的取值范围 ⇔ 函数 y=kx + b ( k ≠0) 中 , y ⑩ 　　 0( y ⑪ 　 　 0) 时 x 的取值 ;  (2) 如图 10-1, 不等式 k 1 x + b 1 >k 2 x + b 2 的解集是 x>m ; 不等式 k 1 x + b 1 ≤ k 2 x + b 2 的解集是 ⑫ 　　　 .  > < x ≤ m 图 1 0 -1 考点五　一次函数的应用 1 . 图象类问题 : 注意利用图象上已知的特殊两点的坐标 , 运用待定系数法求出一次函数的解析式 , 注意写上自变量的取值范围 , 自变量的取值要符合实际意义 . 2 . 表格类问题 : 注意根据表中的数据 , 在坐标系中描出各点 , 分析两变量符合的函数类型 , 再设出表达式 , 用待定系数法求解 . 1 . [2019· 益阳 ] 下列函数中 , y 总随 x 的增大而减小的是 ( 　　 ) A .y= 4 x B .y= -4 x C .y=x -4 D .y=x 2 2 . [2019· 扬州 ] 若点 P 在一次函数 y= - x +4 的图象上 , 则点 P 一定不在 ( 　　 ) A . 第一象限 B . 第二象限 C . 第三象限 D . 第四象限 题组一　必会题 对点演练 B C 3 . [2019· 杭州 ] 已知一次函数 y 1 =ax + b 和 y 2 =bx + a ( a ≠ b ), 函数 y 1 和 y 2 的图象可能是 ( 　　 ) 图 10-2 [ 答案 ] A 　 [ 解析 ] ①当 a> 0, b> 0 时 , y 1 , y 2 的图象都经过第一、二、三象限 ; ②当 a< 0, b< 0 时 , y 1 , y 2 的图象都经过第二、三、四象限 ; ③当 a< 0, b> 0 时 , y 1 的图象经过第一、二 、四象限 , y 2 的图象经过第一、三、四象限 ; ④当 a> 0, b< 0 时 , y 1 的图象经过第一、三、四象限 , y 2 的图象经过第一、二、四象限 . 满足题意的只有 A . 4 . [2018· 荆州 ] 已知 : 将直线 y=x -1 向上平移 2 个单位长度后得到直线 y=kx + b , 则下列关于直线 y=kx + b 的说法正确的是 ( 　　 ) A . 经过第一、二、四象限 　 B . 与 x 轴交于 (1,0) C . 与 y 轴交于 (0,1) 　 D .y 随 x 的增大而减小 C D 图 10-3 6 . 直线 y= 3 x +1 向下平移 2 个单位长度 , 所得直线的解析式是 ( 　　 ) A .y= 3 x +3 B .y= 3 x -2 C .y= 3 x +2 D .y= 3 x -1 题组二　易错题 【 失分点 】 一次函数 y=kx + b 的图象是通过 y=kx 的图象平移得到的 , 易忽略平移方向与系数关系而出错 ; 由一次函数的性质求其表达式时 , 考虑不周 , 导致漏解 ; 由线段的长度或图形的面积求 k , b 的值时 , 如果没有指明图象的具体位置 , 这时要分情况讨论 , 否则易漏解 . D 7 . 若一次函数 y=kx + b 的图象经过点 (-1,-3), 且与 x 轴和 y 轴的交点到原点的距离相等 , 那么它的解析式不可能是 ( 　　 ) A .y=x -2 B .y= -3 x -6 C .y= 3 x D .y= - x -4 [ 答案 ] B 　 [ 解析 ] 由题意得 : ①若 k 的值为 1 或 -1, 将 (-1,-3) 代入 A 选项 , 得 y= -3, x -2 = -3, 符合题意 ; 将 (-1,-3) 代入 D 选项 , 得 y= -3,- x -4 = -3, 符合题意 ; ② k ≠±1, b= 0 . 将 (-1,-3) 代入 C 选项 , 得 y= -3,3 x= -3, 符合题意 . 只有 B 选项 k 既不等于 ±1, b 也不为 0, 不符合题意 . 9 或 1 8 . 已知一次函数 y=kx + b , 且当 -3≤ x ≤1 时 ,1≤ y ≤9, 则 k + b 的值为 　　　　 .  考向一　一次函数的图象与性质 例 1 一次函数 y= ( m -1) x +( m -2) 的图象上有点 M ( x 1 , y 1 ) 和点 N ( x 2 , y 2 ), 且 x 1 >x 2 , 下列叙述正确的是 ( 　　 ) A . 若该函数图象交 y 轴于正半轴 , 则 y 1 0, 故 m -1 > 0, 若 x 1 >x 2 , 则 y 1 >y 2 , 故 A 错误 ; 把 x= -1 代入 y= ( m -1) x +( m -2), 得 y= -1, 则该函数图象必经过点 (-1,-1), 故 B 正确 ; 当 m> 2 时 , m -1 > 0, m -2 > 0, 函数图象过第一、二、三象限 , 不过第四象限 , 故 C 错误 ; 函数图象向上平移 1 个单位长度后 , 函数变为 y= ( m -1) x +( m -1), 所以当 y= 0 时 , x= -1, 故函数图象向上平移 1 个单位长度后 , 会与 x 轴负半轴有交点 , 故 D 错误 . 故选 B . 【 方法点析 】 对于一次函数 y=kx + b ( k ≠0), k 和 b 的符号作用 : k 的符号决定函数的增减性 , k> 0 时 , y 随 x 的增大而增大 , k< 0 时 , y 随 x 的增大而减小 ; b 的符号决定图象与 y 轴的交点在 x 轴上方还是下方 ( 上正下负 ) . | 考向精练 | 1 . 已知一次函数 y=kx + b ( k , b 为常数 , k ≠0) 的图象经过第一、三、四象限 , 则下列结论正确的是 ( 　　 ) A .kb> 0 B .kb< 0 C .k + b> 0 D .k + b< 0 B 2 . 点 P 1 ( x 1 , y 1 ) 和点 P 2 ( x 2 , y 2 ) 是一次函数 y= -4 x +3 图象上的两个点 , 且 x 1 y 2 B .y 1 >y 2 > 0 C .y 1 1 时 , y< 0; ②它的图象经过第一、二、三象限 ; ③它的图象必经过点 (-2,2); ④ y 的值随 x 的增大而增大 . 其中正确结论的个数是 ( 　　 ) A . 1 B . 2 C . 3 D . 4 A A [ 答案 ] D 考向二　用待定系数法求一次函数解析式 例 2 已知直线 l 1 与 x 轴的正半轴交于点 A , 与 y 轴的负半轴交于点 B , OA= 2, OB= 4, 直线 l 2 的函数解析式为 x= 4, 与 x 轴交于点 D , 两直线相交于点 C. (1) 求直线 l 1 对应的函数解析式和点 C 的坐标 ; (2) 点 P 是直线 l 2 上的一点 , 且 DP= 2, 过点 P 作 PE ∥ x 轴 , 交直线 l 1 于点 E , 求线段 PE 的长 . 例 2 已知直线 l 1 与 x 轴的正半轴交于点 A , 与 y 轴的负半轴交于点 B , OA= 2, OB= 4, 直线 l 2 的函数解析式为 x= 4, 与 x 轴交于点 D , 两直线相交于点 C. (2) 点 P 是直线 l 2 上的一点 , 且 DP= 2, 过点 P 作 PE ∥ x 轴 , 交直线 l 1 于点 E , 求线段 PE 的长 . (2) ∵ DP= 2, ∴点 P 的坐标为 (4,±2) . ∵ PE ∥ x 轴 , ∴点 E 的纵坐标为 ±2 . 当点 E 的纵坐标为 2 时 ,2 = 2 x -4, 解得 x= 3 . ∴点 E 的坐标为 (3,2) . ∴ PE= 4-3 = 1 . 当点 E 的纵坐标为 -2 时 ,-2 = 2 x -4, 解得 x= 1 . ∴点 E 的坐标为 (1,-2) . ∴ PE= 4-1 = 3 . ∴线段 PE 的长为 1 或 3 . | 考向精练 | 1 . [2014· 江西 4 题 ] 直线 y=x +1 与 y= -2 x + a 的交点在第一象限 , 则 a 的取值可以是 ( 　　 ) A . -1 B . 0 C . 1 D . 2 [ 答案 ] D 图 10-4 图 10-4 图 10- 5 图 10- 5 考向三　一次函数与方程、不等式的关系 图 10-6 解 :(1) ∵点 P (1, b ) 在直线 y=x +1 上 , ∴当 x= 1 时 , b= 1+1 = 2 . 图 10-6 【 方法点析 】 解答这类题时 , 一要明确一次函数、一次方程和一元一次不等式的内在联系 , 二要在观察图象时特别关注直线与横轴的交点 , 若两直线相交 , 其交点也就是关键点 . | 考向精练 | 图 10-7 [ 答案 ] A 2 . 如图 10-8, 经过点 B (-2,0) 的直线 y=kx + b 与直线 y= 4 x +2 相交于点 A (-1,-2), 则不等式 4 x +2 y 2 , 求 x 的取值范围 . (2) 当 x< 1 时 , y 1 >y 2 . 结合图象 , 直接写出 k 的取值范围 . 4 . 如图 10-9, 直线 y=kx -6 经过点 A (4,0), 直线 y= -3 x +3 与 x 轴交于点 B , 且两直线交于点 C. 求 :(1) k 的值 ; (2)△ ABC 的面积 . 图 10-9 考向四　一次函数的实际应用 例 4 [2019· 齐齐哈尔 ] 甲、乙两地间的直线公路长为 400 千米 , 一辆轿车和一辆货车分别沿该公路从甲、乙两地以各自的速度匀速相向而行 , 货车比轿车早出发 1 小时 , 途中轿车出现了故障 , 停下维修 , 货车仍继续行驶 ,1 小时后轿车故障排除 , 此时接到通知 , 轿车立刻掉头按原路原速返回甲地 ( 接到通知及掉头时间不计 ), 最后两车同时到达甲地 . 已知两车距各自出发地的距离 y ( 千米 ) 与轿车所用的时间 x ( 小时 ) 的关系如图 10-10 所示 , 请结合图象解答下列问题 : (1) 货车的速度是 　　　　 千米 / 时 ; 轿车的速度是 　　　　 千米 / 时 ; t 的值为 　　　　 ;  图 10-10 (2) 求轿车距其出发地的距离 y ( 千米 ) 与所用时间 x ( 小时 ) 之间的函数解析式 , 并写出自变量 x 的取值范围 ; (3) 请直接写出货车出发多长时间两车相距 90 千米 . 图 10-10 解 :(1) 货车的速度是 50 千米 / 时 , 轿车出发后货车行驶时间为 (400-50)÷50 = 7( 时 ), ∴轿车的速度为 480÷(7-1) = 80( 千米 / 时 ) .t= 240÷80 = 3 . 故答案为 :50;80;3 . 例 4 [2019· 齐齐哈尔 ] 甲、乙两地间的直线公路长为 400 千米 , 一辆轿车和一辆货车分别沿该公路从甲、乙两地以各自的速度匀速相向而行 , 货车比轿车早出发 1 小时 , 途中轿车出现了故障 , 停下维修 , 货车仍继续行驶 ,1 小时后轿车故障排除 , 此时接到通知 , 轿车立刻掉头按原路原速返回甲地 ( 接到通知及掉头时间不计 ), 最后两车同时到达甲地 . 已知两车距各自出发地的距离 y ( 千米 ) 与轿车所用的时间 x ( 小时 ) 的关系如图 10-10 所示 , 请结合图象解答下列问题 : (2) 求轿车距其出发地的距离 y ( 千米 ) 与所用时间 x ( 小时 ) 之间的函数解析式 , 并写出自变量 x 的取值范围 ; 图 10-10 例 4 [2019· 齐齐哈尔 ] 甲、乙两地间的直线公路长为 400 千米 , 一辆轿车和一辆货车分别沿该公路从甲、乙两地以各自的速度匀速相向而行 , 货车比轿车早出发 1 小时 , 途中轿车出现了故障 , 停下维修 , 货车仍继续行驶 ,1 小时后轿车故障排除 , 此时接到通知 , 轿车立刻掉头按原路原速返回甲地 ( 接到通知及掉头时间不计 ), 最后两车同时到达甲地 . 已知两车距各自出发地的距离 y ( 千米 ) 与轿车所用的时间 x ( 小时 ) 的关系如图 10-10 所示 , 请结合图象解答下列问题 : (3) 请直接写出货车出发多长时间两车相距 90 千米 . 图 10-10 (3) 设货车出发 x 小时后两车相距 90 千米 . 根据题意 , 得 50 x +80( x -1) = 400-90 或 50 x +80( x -2) = 400+90, 解得 x= 3 或 5 . 答 : 货车出发 3 小时或 5 小时后两车相距 90 千米 . | 考向精练 | 1 . [2017· 江西 19 题 ] 如图 10-11, 是一种斜挎包 , 其挎带由双层部分、单层部分和调节扣构成 . 小敏用后发现 , 通过调节扣加长或缩短单层部分的长度 , 可以使挎带的长度 ( 单层部分与双层部分长度的和 , 其中调节扣所占的长度忽略不计 ) 加长或缩短 . 设单层部分的长度为 x cm, 双层部分的长度为 y cm, 经测量 , 得到如下数据 : (1) 根据表中数据的规律 , 完成以上表格 , 并直接写出 y 关于 x 的函数解析式 ; 单层部分的长度 x/ cm … 4 6 8 10 … 150 双层部分的长度 y/ cm … 73 72 71 … 图 10-11 (2) 根据小敏的身高和习惯 , 挎带的长度为 120 cm 时 , 背起来正合适 , 请求出此时单层部分的长度 ; (3) 设挎带的长度为 l cm, 求 l 的取值范围 . 解 :(1) 从左至右 , 依次填 70,0; y 关于 x 的函数解析式为 y= -0 . 5 x +75 . 1 . [2017· 江西 19 题 ] 如图 10-11, 是一种斜挎包 , 其挎带由双层部分、单层部分和调节扣构成 . 小敏用后发现 , 通过调节扣加长或缩短单层部分的长度 , 可以使挎带的长度 ( 单层部分与双层部分长度的和 , 其中调节扣所占的长度忽略不计 ) 加长或缩短 . 设单层部分的长度为 x cm, 双层部分的长度为 y cm, 经测量 , 得到如下数据 : (2) 根据小敏的身高和习惯 , 挎带的长度为 120 cm 时 , 背起来正合适 , 请求出此时单层部分的长度 ; 单层部分的长度 x/ cm … 4 6 8 10 … 150 双层部分的长度 y/ cm … 73 72 71 … 图 10-11 (2) 当挎带的长度为 120 cm 时 , x + y= 120, ∴ x -0 . 5 x +75 = 120, 解得 x= 90 . 答 : 此时挎带单层部分的长度为 90 cm . 1 . [2017· 江西 19 题 ] 如图 10-11, 是一种斜挎包 , 其挎带由双层部分、单层部分和调节扣构成 . 小敏用后发现 , 通过调节扣加长或缩短单层部分的长度 , 可以使挎带的长度 ( 单层部分与双层部分长度的和 , 其中调节扣所占的长度忽略不计 ) 加长或缩短 . 设单层部分的长度为 x cm, 双层部分的长度为 y cm, 经测量 , 得到如下数据 : (3) 设挎带的长度为 l cm, 求 l 的取值范围 . 单层部分的长度 x/ cm … 4 6 8 10 … 150 双层部分的长度 y/ cm … 73 72 71 … 图 10-11 (3) 根据题意 , 得 l=x + y= 0 . 5 x +75, ∵ 0≤ x ≤150, ∴ 75≤ l ≤150, 即 l 的取值范围为 75≤ l ≤150 . 2 . [2015· 江西 22 题 ] 甲、乙两人在 100 m 直道 AB 上练习匀速往返跑 , 若甲、乙分别在 A , B 两端同时出发 , 分别到另一个端点处掉头 , 掉头时间不计 . 速度分别为 5 m/s 和 4 m/s . (1) 在坐标系中 , 虚线表示乙离 A 端的距离 s ( 单位 :m) 与运动时间 t ( 单位 :s) 之间的函数图象 (0≤ t ≤200), 请在同一坐标系中用实线画出甲离 A 端的距离 s ( 单位 :m) 与运动时间 t ( 单位 :s) 之间的函数图象 (0≤ t ≤200) . 图 10-12 (2) 根据 (1) 中所画图象 , 完成下列表格 : (3) ①直接写出甲、乙两人分别在第一个 100 m 内 , s 与 t 的函数解析式 , 并指出自变量 t 的取值范围 ; ②求甲、乙第 6 次相遇时 t 的值 . 两人相遇次数 / 次 1 2 3 4 … n 两人所跑路程之和 / m 100 300 … 图 10-12 解 :(1) 甲离 A 端的距离 s ( 单位 :m) 与时间 t ( 单位 :s) 的图象如图 . 2 . [2015· 江西 22 题 ] 甲、乙两人在 100 m 直道 AB 上练习匀速往返跑 , 若甲、乙分别在 A , B 两端同时出发 , 分别到另一个端点处掉头 , 掉头时间不计 . 速度分别为 5 m/s 和 4 m/s . (2) 根据 (1) 中所画图象 , 完成下列表格 : 两人相遇次数 / 次 1 2 3 4 … n 两人所跑路程之和 / m 100 300 … (2) 完成表格如下 : 两人相遇次数 / 次 1 2 3 4 … n 两人所跑路程之和 / m 100 300 500 700 … 200 n -100 2 . [2015· 江西 22 题 ] 甲、乙两人在 100 m 直道 AB 上练习匀速往返跑 , 若甲、乙分别在 A , B 两端同时出发 , 分别到另一个端点处掉头 , 掉头时间不计 . 速度分别为 5 m/s 和 4 m/s . (3) ①直接写出甲、乙两人分别在第一个 100 m 内 , s 与 t 的函数解析式 , 并指出自变量 t 的取值范围 ; ②求甲、乙第 6 次相遇时 t 的值 .