九年级上册数学同步练习22-1-4 第1课时 二次函数y=ax2+bx+c的图象和性质 人教版

九年级上册数学同步练习22-1-4 第1课时 二次函数y=ax2+bx+c的图象和性质 人教版

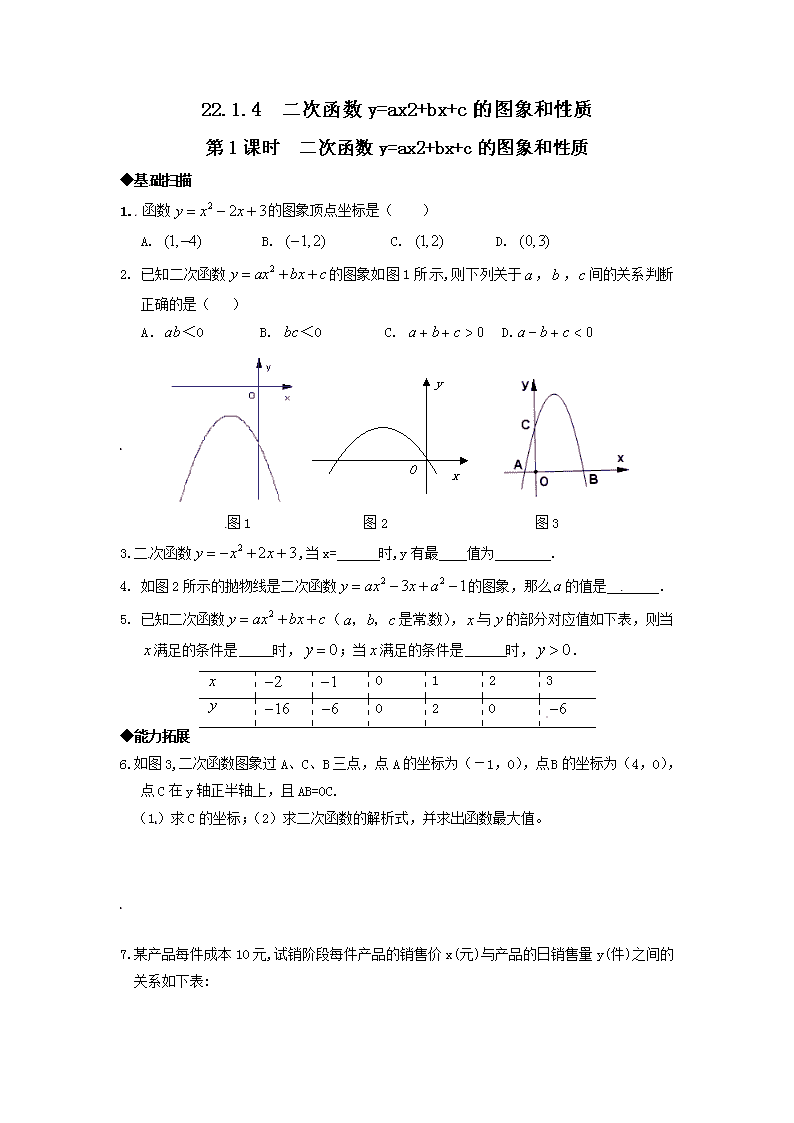
‎22.1.4 二次函数y=ax2+bx+c的图象和性质 第1课时 二次函数y=ax2+bx+c的图象和性质 ‎◆基础扫描 ‎1. 函数的图象顶点坐标是（ ）‎ A. B. C. D. ‎ ‎2. 已知二次函数的图象如图1所示,则下列关于，，间的关系判断正确的是（ ）‎ A．＜0 B. ＜0 C. D. [来源:学科网ZXXK]‎ O y x ‎ 图1 图2 图3‎ ‎3.二次函数,当x= 时,y有最 值为 .‎ ‎4. 如图2所示的抛物线是二次函数的图象，那么的值是 ．‎ ‎5. 已知二次函数（是常数），与的部分对应值如下表，则当满足的条件是 时，；当满足的条件是 时，．‎ ‎0‎ ‎1[来源:Z。xx。k.Com]‎ ‎2[来源:Zxxk.Com]‎ ‎3‎ ‎0‎ ‎2‎ ‎0‎ ‎◆能力拓展 ‎6. 如图3,二次函数图象过A、C、B三点，点A的坐标为（－1，0），点B的坐标为（4，0），点C在y轴正半轴上，且AB=OC.‎ ‎（1）求C的坐标；（2）求二次函数的解析式，并求出函数最大值。‎ ‎7.某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:‎ X(元)‎ ‎15‎ ‎20‎ ‎30‎ ‎…‎ y(件)[来源:学科网]‎ ‎25‎ ‎20‎ ‎10‎ ‎…‎ ‎ ‎ 若日销售量y是销售价x的一次函数.‎ ‎(1)求出日销售量y(件)是销售价x(元)的函数关系式;‎ ‎(2)要使每日的销售利润最大,每件产品的销售价应定为多少元? 此时每日的销售利润是多少元?‎ ‎[来源:学科网]‎ ‎◆创新学习 ‎8．如图，对称轴为直线x＝的抛物线经过点A（6，0）和B（0，4）．‎ ‎（1）求抛物线解析式及顶点坐标；‎ ‎（2）设点E（x，y）是抛物线上一动点，且位于第四象限，四边形OEAF是以OA为对角线的平行四边形，求四边形OEAF的面积S与x之间的函数关系式，并写出自变量x的取值范围；‎ ‎（3）①当四边形OEAF的面积为24时，请判断OEAF是否为菱形？‎ ‎②是否存在点E，使四边形OEAF为正方形？若存在，求出点E的坐标；若不存在，请说明理由．‎ 参考答案 ‎1．C 2．D 3． 大 4 4．－1 ‎ ‎5．0或2 0＜＜2 ‎ ‎6．(1)C(0,5) ‎ ‎ (2) ‎ ‎7．(1)设此一次函数关系式为,‎ 则{,解得 ‎ 故一次函数的关系式为.‎ ‎(2)设所获利润为元,‎ 则 ‎ 所以产品的销售价应定为25元,此时每日的销售利润为225元． ‎ ‎8．（1）由抛物线的对称轴是，可设解析式为．‎ 把A、B两点坐标代入上式，得 ‎ 解之，得 故抛物线解析式为，顶点为 ‎（2）∵点在抛物线上，位于第四象限，且坐标适合.‎ ‎，‎ ‎∴y<0，即 －y>0,－y表示点E到OA的距离．‎ ‎∵OA是的对角线，‎ ‎∴．‎ 因为抛物线与轴的两个交点是（1，0）的（6，0），‎ 所以，自变量的取值范围是1＜＜6．[来源:学科网ZXXK]‎ ‎①根据题意，当S = 24时，即．‎ 化简，得 解之，得 故所求的点E有两个，分别为E1（3，－4），E2（4，－4）．‎ 点E1（3，－4）满足OE = AE，所以是菱形；‎ 点E2（4，－4）不满足OE = AE，所以不是菱形．‎ ‎②当OA⊥EF，且OA = EF时，是正方形，‎ 此时点E的坐标只能是（3，－3）．‎ 而坐标为（3，－3）的点不在抛物线上，‎ 故不存在这样的点E，使为正方形．‎