2019-2020学年山东省济南市市中区九年级(上)期中数学试卷
2019-2020学年山东省济南市市中区九年级(上)期中数学试卷
一、选择题(本大题共12小题,每小题3分,共36分)
1. 用配方法解方程x2−2x−5=0时,原方程应变形为( )
A.(x+1)2=6 B.(x−1)2=6 C.(x+2)2=9 D.(x−2)2=9
2.
根据下面表格中的对应值:
x
3.23
3.24
3.25
3.26
ax2+bx+c
−0.06
−0.02
0.03
0.09
判断方程ax2+bx+c=0(a≠0,a,b,c为常数)的一个解x的范围是( )
A.3
y1>0 D.y1>y2>0
10. (人教版)如图,直线y=x与双曲线y=kx(k>0)的一个交点为A,且OA=2,则k的值为( )
A.1 B.2 C.2 D.22
第21页 共22页 ◎ 第22页 共22页
11. 如图,在平面直角坐标系中,Rt△ABO的顶点O与原点重合,顶点B在x轴上,∠ABO=90∘,OA与反比例函数y=kx的图象交于点D,且OD=2AD,过点D作x轴的垂线交x轴于点C.若S四边形ABCD=10,则k的值为( )
A.−16 B.16 C.−15 D.15
12. 如图,在边长为2的正方形ABCD中,点E是边AD中点,点F在边CD上,且FE⊥BE,设BD与EF交于点G,则△DEG的面积是( )
A.15 B.16 C.17 D.18
二、填空题(本大题共6小题,每小题3分,共18分)
若yx=34,则x+yx的值为________.
如果关于x的方程x2−6x+m=0有两个相等的实数根,那么m=________.
点P既在反比例函数y=−3x(x>0)的图象上,又在一次函数y=−x−2的图象上,则P点的坐标是________.
反比例函数y=m−2x的图象在第二、四象限,那么实数m的取值范围是________.
如图所示,在平行四边形ABCD中,AC与BD相交于O,E为OD的中点,连接AE并延长交CD于点F,则DF:FC等于________.
如图,正方形ABCD的边CD在正方形ECGF的边CE上,O是EG的中点,∠EGC的平分线GH过点D,交BE于点H,连接OH,FH,EG与FH交于点M,对于下面四个结论:
①GH⊥BE;②BG=EG;③△MFG为等腰三角形;④DE:AB=1+2,
其中正确结论的序号为________.
二、解答题(本大题共66分)
解方程
(1)x2−4x−1=0;
(2)x2+3x−2=0;
(3)2x2+3x+3=0
已知关于x的方程x2+(2k−1)x+k2−1=0有两个实数根x1,x2.
(1)求实数k的取值范围;
(2)若x1,x2满足x12+x22=16+x1x2,求实数k的值.
某服装店出售某品牌的棉衣,进价为100元/件,当售价为150元/件时,平均每天可卖30件;为了尽快减少库存迎接“元旦”的到来,商店决定降价销售,增加利润,经调查每件降价5元,则每天可多卖10件,现要想平均每天获利2000元,且让顾客得到实惠,那么每件棉衣应降价多少元?
第21页 共22页 ◎ 第22页 共22页
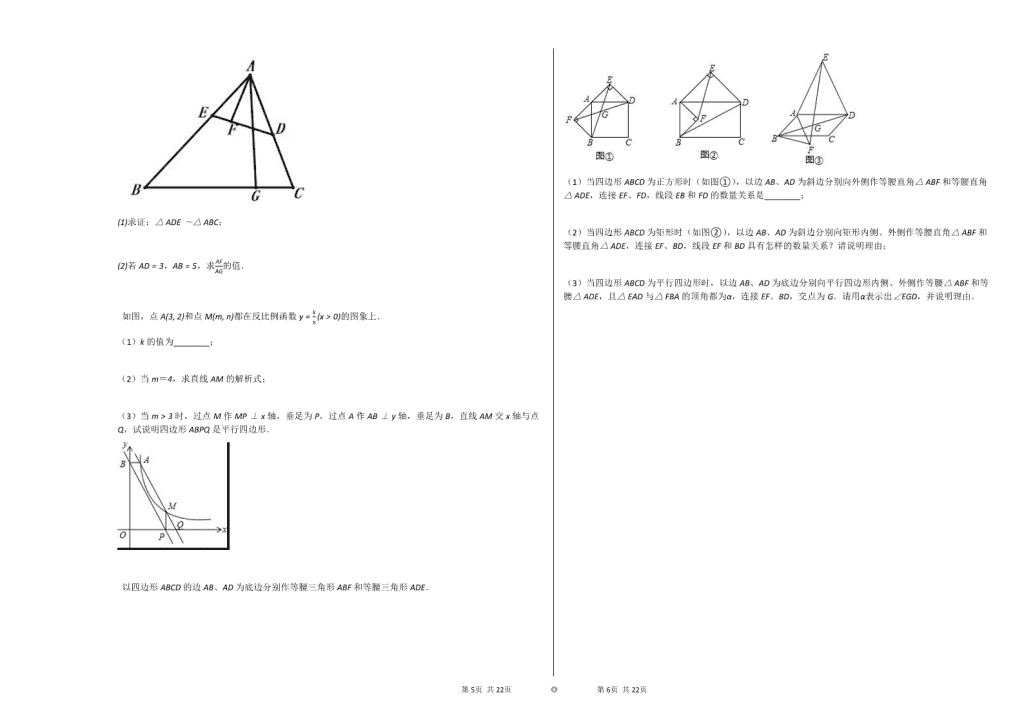
如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∼△ABC;
(2)若AD=3,AB=5,求AFAG的值.
如图,点A(3, 2)和点M(m, n)都在反比例函数y=kx(x>0)的图象上.
(1)k的值为________;
(2)当m=4,求直线AM的解析式;
(3)当m>3时,过点M作MP⊥x轴,垂足为P,过点A作AB⊥y轴,垂足为B,直线AM交x轴与点Q,试说明四边形ABPQ是平行四边形.
以四边形ABCD的边AB、AD为底边分别作等腰三角形ABF和等腰三角形ADE.
(1)当四边形ABCD为正方形时(如图①),以边AB、AD为斜边分别向外侧作等腰直角△ABF和等腰直角△ADE,连接EF、FD,线段EB和FD的数量关系是________;
(2)当四边形ABCD为矩形时(如图②),以边AB、AD为斜边分别向矩形内侧、外侧作等腰直角△ABF和等腰直角△ADE,连接EF、BD,线段EF和BD具有怎样的数量关系?请说明理由;
(3)当四边形ABCD为平行四边形时,以边AB、AD为底边分别向平行四边形内侧、外侧作等腰△ABF和等腰△ADE,且△EAD与△FBA的顶角都为α,连接EF、BD,交点为G.请用α表示出∠EGD,并说明理由.
第21页 共22页 ◎ 第22页 共22页
参考答案与试题解析
2019-2020学年山东省济南市市中区九年级(上)期中数学试卷
一、选择题(本大题共12小题,每小题3分,共36分)
1.
【答案】
B
【考点】
解一元二次方程-配方法
【解析】
方程常数项移到右边,两边加上1变形即可得到结果.
【解答】
解:方程移项得x2−2x=5,
配方得x2−2x+1=6,
即(x−1)2=6.
故选B.
2.
【答案】
C
【考点】
估计一元二次方程的近似解
【解析】
根据表中数据得到x=3.24时,ax2+bx+c=−0.02;x=3.25时,ax2+bx+c=0.01,则x取2.24到2.25之间的某一个数时,使ax2+bx+c=0,于是可判断关于x的方程ax2+bx+c=0(a≠0)的一个解x的范围是3.240,函数图象位于第一,三象限.
故选A.
9.
【答案】
D
【考点】
反比例函数图象上点的坐标特征
反比例函数的性质
【解析】
把两点P1(1, y1)和P2(2, y2)分别代入反比例函数y=−1x求出y2、y1的值即可.
【解答】
解:把点P1(1, y1)代入反比例函数y=1x得,y1=1;
点P2(2, y2)代入反比例函数y=1x得,y2=12;
∵ 1>12>0,
∴ y1>y2>0.
故选D.
10.
【答案】
B
【考点】
反比例函数与一次函数的综合
【解析】
A在直线y=x上,且OA=2,可求得A点坐标为(2, 2)把已知点的坐标代入解析式可得,k=2.
【解答】
设A(x, y),则y=xy=kxx2+y2=4 ,
解得k=2.
11.
【答案】
A
【考点】
反比例函数系数k的几何意义
【解析】
证△DCO∽△ABO,推出DCAB=OCOB=ODOA=23,求出S△ODCS△OAB=(23)2=49,求出S△ODC=8,根据三角形面积公式得出12OC×CD=8,求出OC×CD=16即可.
【解答】
∵ OD=2AD,
∴ ODOA=23,
∵ ∠ABO=90∘,DC⊥OB,
∴ AB // DC,
∴ △DCO∽△ABO,
∴ DCAB=OCOB=ODOA=23,
∴ S△ODCS△OAB=(23)2=49,
∵ S四边形ABCD=10,
∴ S△ODC=8,
∴ 12OC×CD=8,
第21页 共22页 ◎ 第22页 共22页
OC×CD=16,
∴ k=−16,
12.
【答案】
B
【考点】
相似三角形的性质与判定
正方形的性质
【解析】
过点G作GM⊥AD于M,如图,先证明△ABE∽△DEF,利用相似比计算出DF=12,再利用正方形的性质判断△DGM为等腰直角三角形得到DM=MG,设DM=x,则MG=x,EM=1−x,然后证明△EMG∽△EDF,则利用相似比可计算出GM,再利用三角形面积公式计算S△DEG即可.
【解答】
过点G作GM⊥AD于M,如图,
∵ FE⊥BE,
∴ ∠AEB+∠DEF=90∘,
而∠AEB+∠ABE=90∘,
∴ ∠ABE=∠DEF,
而∠A=∠EDF,
∴ △ABE∽△DEF,
∴ AB:DE=AE:DF,即2:1=1:DF,
∴ DF=12,
∵ 四边形ABCD为正方形,
∴ ∠ADB=45∘,
∴ △DGM为等腰直角三角形,
∴ DM=MG,
设DM=x,则MG=x,EM=1−x,
∵ MG // DF,
∴ △EMG∽△EDF,
∴ MG:DF=EM:ED,即x:12=(1−x):1,解得x=13,
∴ S△DEG=12×1×13=16.
二、填空题(本大题共6小题,每小题3分,共18分)
【答案】
74
【考点】
比例的性质
【解析】
根据合比性质,可得答案.
【解答】
解:由合比性质,得
x+yx=3+44=74.
故答案为:74.
【答案】
9
【考点】
根的判别式
【解析】
因为一元二次方程有两个相等的实数根,所以△=b2−4ac=0,根据判别式列出方程求解即可.
【解答】
∵ 关于x的方程x2−6x+m=0有两个相等的实数根,
∴ △=b2−4ac=0,
即(−6)2−4×1×m=0,
解得m=9
【答案】
(1, −3)
【考点】
一次函数图象上点的坐标特点
反比例函数图象上点的坐标特征
【解析】
点P既在反比例函数y=−3x(x>0)的图象上,又在一次函数y=−x−2的图象上,则点P的坐标是这两个函数的解.两个函数组成方程组,解这个方程组即可.
【解答】
根据题意可得:−3x=−x−2,则x2+2x−3=0,
即(x−1)(x+3)=0,
解得:x=1或x=−3,
因为x>0,所以x=1,此时y=−3,
所以P点的坐标是(1, −3).
【答案】
m<2
【考点】
反比例函数的性质
【解析】
由于反比例函数y=m−2x的图象在二、四限内,则m−2<0,解得m的取值范围即可.
【解答】
第21页 共22页 ◎ 第22页 共22页
由题意得,反比例函数y=m−2x的图象在二、四象限内,
则m−2<0,
解得m<2.
【答案】
1:2
【考点】
平行四边形的性质
相似三角形的性质与判定
相似三角形的性质
【解析】
先证明△DEF∽△BEA,得出DFAB=13,即可得出结论.
【解答】
∵ 四边形ABCD是平行四边形,
∴ AB // CD,AB=CD,OD=OB,
∴ △DEF∽△BEA,
∴ DFBA=DEBE,
∵ E为OD的中点,
∴ BE=3DE,
∴ DFBA=13,
∴ AB=3DF,
∴ DF:CD=1:3,
∴ DF:FC=1:2.
【答案】
①②③
【考点】
三角形中位线定理
四边形综合题
等腰三角形的判定
全等三角形的性质与判定
等腰直角三角形
【解析】
证明△BCE≅△DCG,即可证得∠BEC=∠DGC,然后根据三角形的内角和定理证得∠EHG=90∘,则HG⊥BE,然后证明△BGH≅△EGH,则H是BE的中点,则OH是△BGE的中位线,根据三角形的中位线定理即可得到HO=12BG,HO // BG,以及∠MOH=∠EGC=45∘,再根据等腰直角三角形的性质,得出OF=12EG,∠OFG=45∘,以及OH=OF,根据∠MHO+∠HOM=∠OFH+∠OFG,即可得出∠FMG=∠MFG,最后根据等腰直角三角形的边角关系,得出DB:AB=2:1,即可得到DE:AB=2:1.
【解答】
∵ 正方形ABCD的边CD在正方形ECGF的边CE上,
∴ ∠BCE=∠DCG=90∘,BC=DC,EC=GC,
∴ △BCE≅△DCG(SAS),
∴ ∠CGD=∠CEB,
又∵ ∠CDG=∠HDE,
∴ ∠EHD=∠GCD=90∘,
∴ GH⊥BE,故①正确;
∵ ∠EGC的平分线GH过点D,
∴ ∠BGH=∠EGH,
∵ GH⊥BE,
∴ ∠BHG=∠EHG=90∘,
∴ △BGH≅△EGH(ASA),
∴ BG=EG,故②正确;
∵ BG=EG,GH⊥BE,
∴ H为BE的中点,
又∵ O是EG的中点,
∴ HO是△BEG的中位线,
∴ HO=12BG,HO // BG,
∴ ∠MOH=∠EGC=45∘,
如图,连接FO,
∵ O是EG的中点,
∴ 等腰Rt△EFG中,OF=12EG,∠OFG=45∘,
∴ OH=OF,
∴ ∠OHF=∠OFH,
∴ ∠MHO+∠HOM=∠OFH+∠OFG,即∠FMG=∠MFG,
∴ FG=MG,即△MFG是等腰三角形,故③正确;
如图,连接BD,
∵ HG垂直平分BE,
∴ DE=DB,
∵ Rt△ABD中,DB:AB=2:1,
∴ DE:AB=2:1,故④错误;
二、解答题(本大题共66分)
【答案】
∵ x2−4x−1=0,
∴ x2−4x=1,
∴ x2−4x+4=5,
∴ (x−2)2=5,
∴ x=2±5;
∵ x2+3x−2=0,
∴ a=1,b=3,c=−2,
∴ △=9+8=17,
∴ x=−3±172;
∵ 2x2+3x+3=0,
∴ a=
第21页 共22页 ◎ 第22页 共22页
2,b=3,c=3,
∴ △=9−24=−15<0,
故原方程无解
【考点】
解一元二次方程-配方法
解一元二次方程-公式法
解一元二次方程-因式分解法
【解析】
(1)根据配方法即可求出答案;
(2)根据公式法即可求出答案;
(3)根据公式法即可求出答案.
【解答】
∵ x2−4x−1=0,
∴ x2−4x=1,
∴ x2−4x+4=5,
∴ (x−2)2=5,
∴ x=2±5;
∵ x2+3x−2=0,
∴ a=1,b=3,c=−2,
∴ △=9+8=17,
∴ x=−3±172;
∵ 2x2+3x+3=0,
∴ a=2,b=3,c=3,
∴ △=9−24=−15<0,
故原方程无解
【答案】
解:(1)∵ 关于x的方程x2+(2k−1)x+k2−1=0有两个实数根x1,x2,
∴ Δ=(2k−1)2−4(k2−1)=−4k+5≥0,
解得:k≤54,
∴ 实数k的取值范围为k≤54.
(2)∵ 关于x的方程x2+(2k−1)x+k2−1=0有两个实数根x1,x2,
∴ x1+x2=1−2k,x1⋅x2=k2−1.
∵ x12+x22=(x1+x2)2−2x1⋅x2=16+x1⋅x2,
∴ (1−2k)2−2×(k2−1)=16+(k2−1),即k2−4k−12=0,
解得:k=−2或k=6(不符合题意,舍去).
∴ 实数k的值为−2.
【考点】
根与系数的关系
根的判别式
【解析】
(1)根据方程的系数结合根的判别式,即可得出△=−4k+5≥0,解之即可得出实数k的取值范围;
(2)由根与系数的关系可得x1+x2=1−2k、x1⋅x2=k2−1,将其代入x12+x22=(x1+x2)2−2x1⋅x2=16+x1⋅x2中,解之即可得出k的值.
【解答】
解:(1)∵ 关于x的方程x2+(2k−1)x+k2−1=0有两个实数根x1,x2,
∴ Δ=(2k−1)2−4(k2−1)=−4k+5≥0,
解得:k≤54,
∴ 实数k的取值范围为k≤54.
(2)∵ 关于x的方程x2+(2k−1)x+k2−1=0有两个实数根x1,x2,
∴ x1+x2=1−2k,x1⋅x2=k2−1.
∵ x12+x22=(x1+x2)2−2x1⋅x2=16+x1⋅x2,
∴ (1−2k)2−2×(k2−1)=16+(k2−1),即k2−4k−12=0,
解得:k=−2或k=6(不符合题意,舍去).
∴ 实数k的值为−2.
【答案】
每件棉衣应降价25元
【考点】
一元二次方程的应用
【解析】
设每件棉衣应降价x元,根据平均每天获利2000元,即可得出关于x的一元二次方程,解方程即可得出x的值,取其中较大的值,此题得解.
【解答】
设每件棉衣应降价x元,由题意得:(150−x−100)(30+10×x5)=2000,
整理得:x2−35x+250=0,
解得:x1=10,x2=25,
∵ 25>10,
∴ x的值选25.
【答案】
(1)证明:∵ AG⊥BC,AF⊥DE,
∴ ∠AFE=∠AGC=90∘,
∵ ∠EAF=∠GAC,
∴ ∠AED=∠ACB,
∵ ∠EAD=∠BAC,
∴ △ADE∼△ABC.
第21页 共22页 ◎ 第22页 共22页
(2)解:方法一:由(1)可知:△ADE∼△ABC,
∴ ADAB=AEAC=35
由(1)可知:∠AFE=∠AGC=90∘,
又∵∠EAF=∠GAC,
∴ △EAF∼△CAG,
∴ AFAG=AEAC=35.
方法二:∵ AG⊥BC,AF⊥DE,
△ADE∼△ABC,
∴ AFAG=ADAB=35.
【考点】
相似三角形的性质与判定
【解析】
(1)由于AG⊥BC,AF⊥DE,所以∠AFE=∠AGC=90∘,从而可证明∠AED=∠ACB,进而可证明△ADE∽△ABC;
(2)△ADE∽△ABC,ADAB=AEAC,又易证△EAF∽△CAG,所以AFAG=AEAC,从而可知AFAG=ADAB.
【解答】
(1)证明:∵ AG⊥BC,AF⊥DE,
∴ ∠AFE=∠AGC=90∘,
∵ ∠EAF=∠GAC,
∴ ∠AED=∠ACB,
∵ ∠EAD=∠BAC,
∴ △ADE∼△ABC.
(2)解:方法一:由(1)可知:△ADE∼△ABC,
∴ ADAB=AEAC=35
由(1)可知:∠AFE=∠AGC=90∘,
又∵∠EAF=∠GAC,
∴ △EAF∼△CAG,
∴ AFAG=AEAC=35.
方法二:∵ AG⊥BC,AF⊥DE,
△ADE∼△ABC,
∴ AFAG=ADAB=35.
【答案】
6
将x=4代入反比例解析式y=6x得:y=32,即M(4, 32),
设直线AM解析式为y=ax+b,
把A与M代入得:3a+b=24a+b=32 ,
解得:a=−12,b=72,
∴ 直线AM解析式为y=−12x+72;
把M(m, n)代入y=6x得m=6n,
∴ M(6n, n)
把M,A点坐标代入y=kx+b得
k=−n3,b=2+n,
∴ 直线AM解析式为y=−n3x+2+n,
∴ Q(6n+3, 0),
∵ MP⊥x轴,
∴ P(6n, 0)
∴ PQ=OQ−OP=3,
∵ AB⊥y轴,
∴ AB // PQ,AB=3,
∴ AB=PQ,
∴ 四边形ABPQ是平行四边形.
【考点】
反比例函数与一次函数的综合
【解析】
(1)将A坐标代入反比例解析式求出k的值即可;
(2)由k的值确定出反比例解析式,将x=3代入反比例解析式求出y的值,确定出M坐标,设直线AM解析式为y=ax+b,将A与M坐标代入求出a与b的值,即可确定出直线AM解析式;
(3)由MP垂直于x轴,AB垂直于y轴,得到M与P横坐标相同,P与Q纵坐标相同,表示出P与Q坐标于是得到结论.
【解答】
将A(3, 2)代入反比例解析式得:k=6;
故答案为:6;
将x=4代入反比例解析式y=6x得:y=32,即M(4, 32),
设直线AM解析式为y=ax+b,
把A与M代入得:3a+b=24a+b=32 ,
解得:a=−12,b=72,
∴ 直线AM解析式为y=−12x+72;
把M(m, n)代入y=6x得m=6n,
∴ M(6n, n)
把M,A点坐标代入y=kx+b得
k=−n3,b=2+n,
∴ 直线AM解析式为y=−n3x+2+n,
∴ Q(6n+3, 0),
∵ MP⊥x轴,
∴ P(6n, 0)
∴ PQ=OQ−OP=3,
∵ AB⊥y轴,
∴ AB // PQ,
第21页 共22页 ◎ 第22页 共22页
AB=3,
∴ AB=PQ,
∴ 四边形ABPQ是平行四边形.
【答案】
BE=DF
结论:BD=2EF.
证明:如图②中,
∵ △ABF和△ADE是等腰直角三角形,
∴ ADAE=ABAF=2,∠EAD=45∘,∠BAF=45∘,
∵ 四边形ABCD是矩形,
∴ ∠BAD=90∘,
∴ ∠FAD=∠BAD−∠BAF=45∘,
∴ ∠EAF=∠FAD+∠EAD=90∘,
∴ ∠EAF=∠BAD=90∘,
∴ △EAF∼△DAB,
∴ BDEF=ADAE=2;
∴ BD=2EF.
如图③,设EF与AD的交点为P点,
∵ 等腰三角形ABF和ADE的顶角∠AED=∠AFB=α,
∴ ∠EAD=∠EDA=∠FAB=∠FBA=90∘−12α,
∴ △EAD∼△FAB,
∴ EAAF=ADAB,
∴ EAAD=AFAB,
∵ ∠EAD+∠DAF=∠FAB+∠DAF,
即:∠EAF=∠DAB,
∴ △EAF∼△DAB,
∴ ∠AEF=∠ADB,
又∵ ∠APE=∠GPD,
∴ △PAE∼△PGD,
∴ ∠EGD=∠EAD=90∘−12α.
【考点】
四边形综合题
【解析】
(1)先证明△ABF≅△ADE,再证明F、A、E共线,得四边形BFED是矩形,根据矩形的对角线相等得:BE=DF可得结论;
(2)证明△EAF∼△DAB,列比例式,根据等腰直角三角形斜边与直角边的比可得结论;
(3)设EF与AD的交点为P点,证明△EAD∽△FAB,再证明△EAF∼△DAB,最后证明△PAE∼△PGD,得∠EGD=∠EAD=90∘−12α.
【解答】
如图①,连接BD,
∵ 四边形ABCD是正方形,
∴ AB=AD,∠BAD=90∘,
∵ 等腰直角三角形ABF和ADE,
∴ ∠BAF=∠ABF=∠DAE=∠ADE=45∘,
∴ ∠FAB+∠BAD+∠DAE=180∘,△ABF≅△ADE(ASA),
∴ F、A、E共线,BF=DE,
∵ ∠AFB+∠AED=90∘+90∘=180∘,
∴ DE // BF,
∴ 四边形BFED是矩形,
∴ BE=DF.
故答案为BE=DF.
结论:BD=2EF.
证明:如图②中,
∵
第21页 共22页 ◎ 第22页 共22页
△ABF和△ADE是等腰直角三角形,
∴ ADAE=ABAF=2,∠EAD=45∘,∠BAF=45∘,
∵ 四边形ABCD是矩形,
∴ ∠BAD=90∘,
∴ ∠FAD=∠BAD−∠BAF=45∘,
∴ ∠EAF=∠FAD+∠EAD=90∘,
∴ ∠EAF=∠BAD=90∘,
∴ △EAF∼△DAB,
∴ BDEF=ADAE=2;
∴ BD=2EF.
如图③,设EF与AD的交点为P点,
∵ 等腰三角形ABF和ADE的顶角∠AED=∠AFB=α,
∴ ∠EAD=∠EDA=∠FAB=∠FBA=90∘−12α,
∴ △EAD∼△FAB,
∴ EAAF=ADAB,
∴ EAAD=AFAB,
∵ ∠EAD+∠DAF=∠FAB+∠DAF,
即:∠EAF=∠DAB,
∴ △EAF∼△DAB,
∴ ∠AEF=∠ADB,
又∵ ∠APE=∠GPD,
∴ △PAE∼△PGD,
∴ ∠EGD=∠EAD=90∘−12α.
第21页 共22页 ◎ 第22页 共22页