相似三角形判定定理的证明教案2

相似三角形判定定理的证明教案2

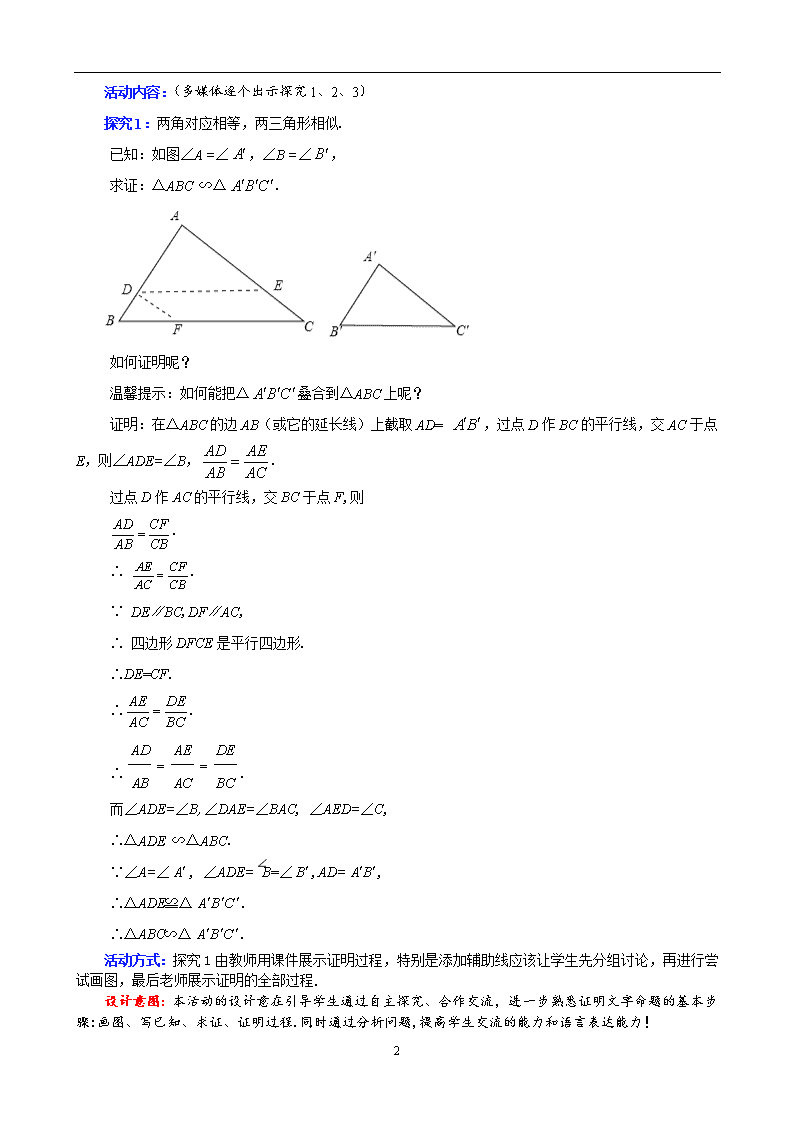
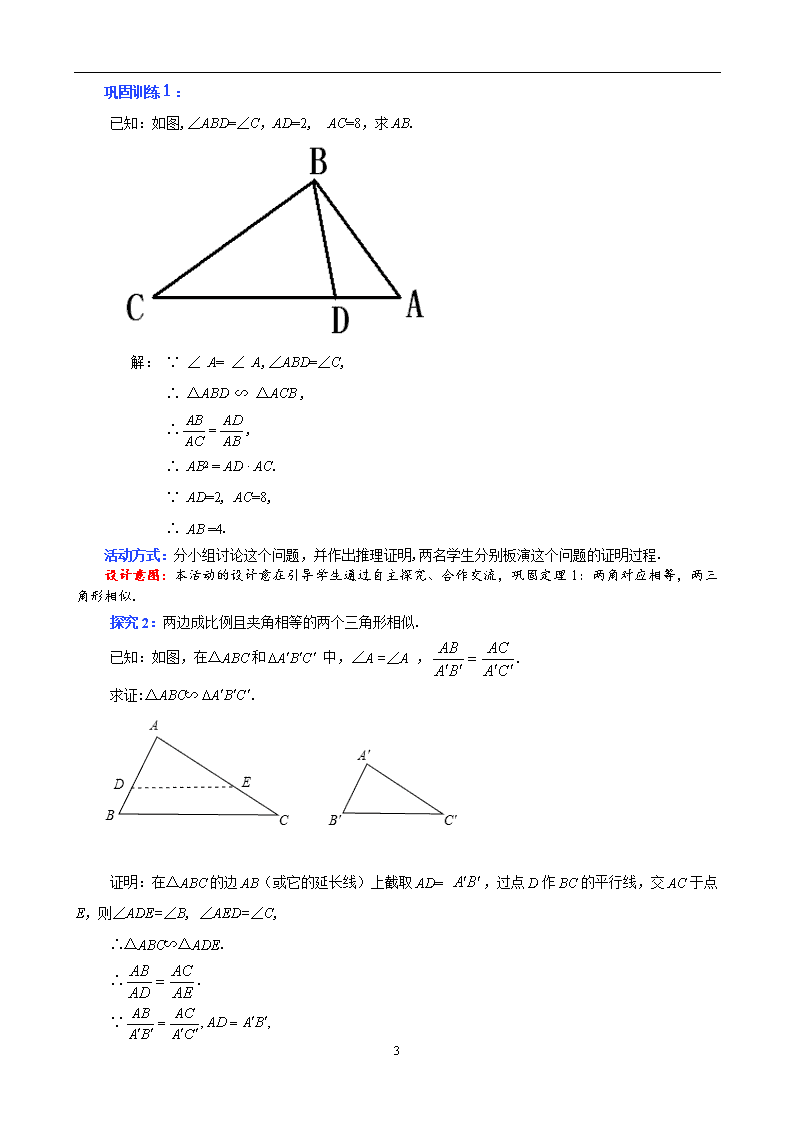
课题：4.5相似三角形判定定理的证明 课型：新授课 教学目标：‎ ‎1. 以问题的形式，创设一个有利于学生动手和探究的情境，达到学会本节课所学的相似三角形的判定方法. ‎ ‎2. 会证明相似三角形判定定理.‎ ‎3. 培养学生积极的思考、动手、观察的能力，使学生感悟几何知识在生活中的价值.掌握推理证明的方法，发展演绎推理能力.‎ 教学重点与难点：‎ 重点：证明相似三角形判定定理．抓住判定方法的条件，通过已知条件的分析，把握图形的结构特点.‎ 难点：证明相似三角形判定定理．‎ 关键：利用经典题目特别训练，并辅以课件的演示是突破难点的好方法．‎ 课前准备：制作多媒体课件.‎ 教学过程：‎ 一、创设情景，导入新课 活动内容：‎ ‎1.观察并思考，用叠合法证明这两个风筝图形相似.‎ ‎2.相似三角形的判定方法有哪些？‎ ‎3.判定两个三角形全等的方法有哪些？‎ 活动方式：问题1由教师演示动画，并适时强调叠合法在本节课有很大的作用，学生观察思考完成.对于问题2、3直接让学生口答：SAS，ASA，AAS，SSS，（HL）；（1）两角对应相等，两三角形相似. ‎ ‎（2）两边对应成比例且夹角相等,两三角形相似.（3）三边对应成比例,两三角形相似.‎ 设计意图: 利用学生感兴趣的动画演示开始本节课的学习和探讨，更有助于培养学生的学习兴趣，激发学生的求知欲，让学生在不知不觉中感受学习数学的乐趣，同时也让学生进一步回顾相关知识点，为进行新课做好准备.‎ 二、探究学习，感悟新知 6‎ 活动内容：（多媒体逐个出示探究1、2、3）‎ 探究1：两角对应相等，两三角形相似.‎ 已知：如图∠A =∠，∠B =∠， ‎ 求证：△ABC ∽△.‎ 如何证明呢？‎ 温馨提示：如何能把△叠合到△ABC上呢？‎ 证明：在△ABC的边AB（或它的延长线）上截取AD= ，过点D作BC的平行线，交AC于点E，则∠ADE=∠B，.‎ 过点D作AC的平行线，交BC于点F,则 ‎.‎ ‎∴ .‎ ‎∵ DE∥BC,DF∥AC,‎ ‎∴ 四边形DFCE是平行四边形.‎ ‎∴DE=CF.‎ ‎∴.‎ ‎∴.‎ 而∠ADE=∠B,∠DAE=∠BAC, ∠AED=∠C,‎ ‎∴△ADE ∽△ABC.‎ ‎∵∠A=∠, ∠ADE=∠B=∠,AD=,‎ ‎∴△ADE≌△.‎ ‎∴△ABC∽△.‎ 活动方式：探究1由教师用课件展示证明过程，特别是添加辅助线应该让学生先分组讨论，再进行尝试画图，最后老师展示证明的全部过程.‎ 设计意图：本活动的设计意在引导学生通过自主探究、合作交流，进一步熟悉证明文字命题的基本步骤:画图、写已知、求证、证明过程.同时通过分析问题,提高学生交流的能力和语言表达能力！‎ 6‎ 巩固训练１：‎ 已知：如图,∠ABD=∠C，AD=2, AC=8，求AB. ‎ 解： ∵ ∠ A= ∠ A,∠ABD=∠C, ‎ ‎ ∴ △ABD ∽ △ACB ,‎ ‎ ∴,‎ ‎ ∴ AB2 = AD · AC.‎ ‎ ∵ AD=2, AC=8,‎ ‎ ∴ AB =4.‎ 活动方式：分小组讨论这个问题，并作出推理证明,两名学生分别板演这个问题的证明过程.‎ 设计意图：本活动的设计意在引导学生通过自主探究、合作交流，巩固定理1：两角对应相等，两三角形相似.‎ 探究2：两边成比例且夹角相等的两个三角形相似.‎ 已知：如图，在△ABC和 中，∠A =∠A ，.‎ 求证:△ABC∽.‎ 证明：在△ABC的边AB（或它的延长线）上截取AD= ，过点D作BC的平行线，交AC于点E，则∠ADE=∠B, ∠AED=∠C,‎ ‎∴△ABC∽△ADE.‎ ‎∴.‎ ‎∵‎ 6‎ ‎∴.‎ ‎∴.‎ ‎∴.‎ 而 ‎∴△ADE≌.‎ ‎∴△ABC∽。‎ 活动方式: 探究2由教师用课件展示证明过程，特别是添加辅助线应该让学生借助探究1先分组讨论，再进行尝试画图，并由两名学生板书证明过程,最后老师展示证明的全部过程加以矫正.‎ 设计意图：由于学生已经有了探究1的基本方法和思路,因此,探究2处理起来应该很顺利,可以大胆放手给学生,这样更能激发学生的求知欲望,让学生在不知不觉中感受学习数学的乐趣和成功的喜悦.‎ 探究3：三 边成比例的两个三角形相似.‎ 已知:如图,在△ABC和△ 中, .‎ 求证：△ABC ∽△.‎ 证明:在△ABC的边AB,AC(或它们的延长线) 上分别截取,,连接DE.‎ ‎∵‎ ‎∴‎ 而 ‎∴△ABC ∽△ADE,‎ ‎∴‎ 又 ‎∴‎ ‎∴‎ ‎∴‎ ‎∴△ADE≌△.‎ ‎∴△ABC ∽△.‎ 6‎ 活动方式: 探究3应该让学生借助探究1、２先分组讨论，再进行尝试画图，并由两名学生板书证明过程,由教师用课件展示证明过程，特别是添加辅助线，学生完全可以模仿探究２进行.最后老师展示证明的全部过程加以矫正.‎ 设计意图：由于学生已经有了探究1、２的基本方法和思路,因此,探究３处理起来应该很顺利,可以大胆放手给学生,这样更能激发学生的求知欲望,让学生在不知不觉中感受学习数学的乐趣和成功的喜悦.‎ 巩固训练2:‎ 已知：如图，在四边形ABCD中，∠B=∠ACD，AB=6，BC=4，AC=5，CD= 7，‎ 求AD的长. ‎ 解：‎ ‎∴.‎ 又,‎ ‎∴∽,‎ ‎∴,‎ ‎∴.‎ 活动方式：分小组讨论这个问题，并作出推理证明,两名学生分别板演这个问题的证明过程.‎ 设计意图：本活动的设计意在引导学生通过自主探究、合作交流，巩固定理1、2、3.‎ 三、课时小结，畅谈收获 活动：学而不思则罔,通过本章的复习你有哪些收获和体会？‎ 活动方式：首先由学生抢答，通过对定理1、2、3的回顾与梳理，明白知识之间的联系．通过辅助线的添加，找到问题的关键点，抓住规律．强化相似三角形判定定理的证明：1.两角对应相等，两三角形相似；2.三边对应成比例,两三角形相似；3.两边对应成比例且夹角相等,两三角形相似.‎ 设计意图: 通过盘点收获，学生小结了本节课的知识要点及数学方法，进一步加深了对类比学习方法的感受，使知识系统化.‎ 四、达标检测，反馈提高 师：通过本节课的学习，同学们的收获真多！收获的质量如何呢？请完成达标检测题．（多媒体出示）‎ 图(1)‎ 已知：如图(1)，．‎ 求证：．‎ 图(2)‎ ‎2．找出图中所有的相似三角形． ‎ 6‎ 处理方式：学生做完后，教师出示答案，指导学生校对，并统计学生答题情况．学生根据答案进行纠错．‎ 设计意图：学以致用，当堂检测及时获知学生对所学知识掌握情况，并最大限度地调动全体学生学习数学的积极性，使每个学生都能有所收益、有所提高，明确哪些学生需要在课后加强辅导，达到全面提高的目的．‎ 六、布置作业，课堂延伸 必做题：课本 102页 习题4.9 第1、2、3题．‎ 选做题：课本 102页 习题4.9 第4题．‎ 板书设计：‎ ‎§4.5 相似三角形判定定理的证明 探究1:‎ 探究2:‎ 探究3:‎ 投 影 区 学 生 活 动 区 6‎