人教版九年级数学上册专题训练(五)二次函数图象信息的解读与应用

人教版九年级数学上册专题训练(五)二次函数图象信息的解读与应用

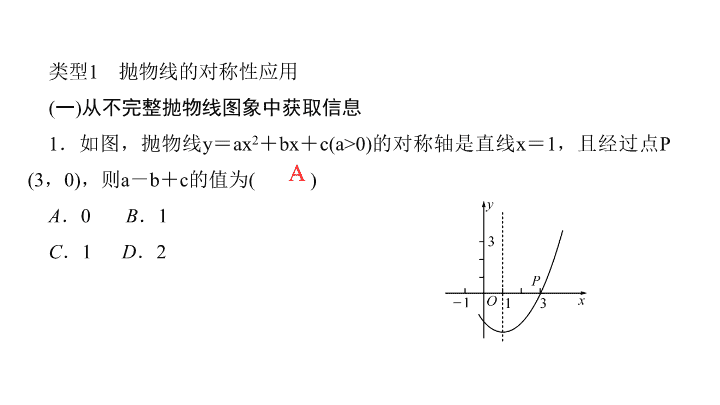
第二十二章　二次函数 人教版 专题训练(五)　二次函数图象信息的解读与应用 类型 1 　抛物线的对称性应用 ( 一 ) 从不完整抛物线图象中获取信息 1 ．如图，抛物线 y ＝ ax 2 ＋ bx ＋ c(a>0) 的对称轴是直线 x ＝ 1 ，且经过点 P(3 ， 0) ，则 a － b ＋ c 的值为 ( ) A ． 0 B ． 1 C ． 1 D ． 2 A 2 ．如图是二次函数 y ＝ ax 2 ＋ bx ＋ c 的部分图象，由图象可知不等式 ax 2 ＋ bx ＋ c>0 的解集是 ( ) A ．－ 1 ＜ x ＜ 5 B ． x ＞ 5 C ． x ＜－ 1 且 x ＞ 5 D ． x ＜－ 1 或 x ＞ 5 A 3 ．抛物线 y ＝ ax 2 ＋ ax ＋ a 2 ＋ 2 的一部分图象如图所示，那么该抛物线在 y 轴右侧与 x 轴交点的坐标是 ( ) A .(0.5 ， 0) B ． (1 ， 0) C ． (2 ， 0) D ． (3 ， 0) C ( 二 ) 求函数解析式 4 ．如图，抛物线 y ＝ x 2 ＋ bx ＋ c 与 y 轴交于点 A(0 ， 2) ，对称轴为直线 x ＝－ 2 ，平行于 x 轴的直线与抛物线交于 B 、 C 两点，点 B 在对称轴左侧， BC ＝ 6. (1) 求此抛物线的解析式； (2) 求直线 AB 的解析式． ( 三 ) 求两线段和的最小值 5 ．如图，抛物线 y ＝ x 2 ＋ 2x ＋ 1 ＋ k 与 x 轴交于 A ， B 两点，与 y 轴交于点 C(0 ，－ 3). (1) 求抛物线的对称轴及 k 的值； (2) 抛物线的对称轴上是否存在一点 P ，使得 PB ＋ PC 的值最小，若存在，求此时点 P 的坐标；若不存在，请说明理由． 解： (1)∵ 抛物线 y ＝ (x ＋ 1) 2 ＋ k 与 y 轴交于点 C(0 ，－ 3) ， ∴－ 3 ＝ 1 ＋ k ，∴ k ＝－ 4 ，∴抛物线的解析式为 y ＝ (x ＋ 1) 2 － 4 ， ∴抛物线的对称轴为 x ＝－ 1 A 7 ．二次函数 y ＝ ax 2 ＋ bx ＋ c(a≠0) 的图象如图所示，则一次函数 y ＝ ax 与一次函数 y ＝ bx － c 在同一坐标系内的图象大致是 ( ) A 8. (2019 · 湖州 ) 已知 a ， b 是非零实数， |a|>|b| ，在同一平面直角坐标系中，二次函数 y 1 ＝ ax 2 ＋ bx 与一次函数 y 2 ＝ ax ＋ b 的大致图象不可能是 ( ) D ( 二 ) 已知函数图象确定 a ， b ， c 及有关式子的符号 9 ．如果二次函数 y ＝ ax 2 ＋ bx ＋ c 的图象如图所示，那么 ( ) A ． a<0 ， b>0 ， c>0 B ． a>0 ， b<0 ， c>0 C ． a>0 ， b<0 ， c<0 D ． a>0 ， b>0 ， c<0 C 10 ． ( 成都中考 ) 在平面直角坐标系 xOy 中，二次函数 y ＝ ax 2 ＋ bx ＋ c 的图象如图所示，下列说法正确的是 ( ) A ． abc ＜ 0 ， b 2 － 4ac ＞ 0 B ． abc ＞ 0 ， b 2 － 4ac ＞ 0 C ． abc ＜ 0 ， b 2 － 4ac ＜ 0 D ． abc ＞ 0 ， b 2 － 4ac ＜ 0 B 11 ．已知二次函数 y ＝ ax 2 ＋ bx ＋ c(a≠0) 的图象如图所示，请结合图象，判断下列各式的符号． ① abc ；② b 2 － 4ac ；③ a ＋ b ＋ c ；④ a － b ＋ c. ( 三 ) 根据抛物线的特征判断有关方程 ( 等式 ) 和不等式是否成立 12 ． (2019 · 鄂州 ) 二次函数 y ＝ ax 2 ＋ bx ＋ c 的图象如图所示，对称轴是直线 x ＝ 1. 下列结论：① abc ＜ 0 ；② 3a ＋ c ＞ 0 ；③ (a ＋ c) 2 － b 2 ＜ 0 ；④ a ＋ b≤m(am ＋ b)(m 为实数 ). 其中结论正确的个数为 ( ) A ． 1 个 B ． 2 个 C ． 3 个 D ． 4 个 C 13 ． ( 孝感中考 ) 如图是抛物线 y ＝ ax 2 ＋ bx ＋ c(a≠0) 的部分图象，其顶点坐标为 (1 ， n) ，且与 x 轴的一个交点在点 (3 ， 0) 和 (4 ， 0) 之间．下列结论： ① a － b ＋ c>0 ；② 3a ＋ b ＝ 0 ；③ b 2 ＝ 4a(c － n) ；④一元二次方程 ax 2 ＋ bx ＋ c ＝ n － 1 有两个不相等的实数根，其中正确结论的个数是 ( ) A ． 1 个 B ． 2 个 C ． 3 个 D ． 4 个 C 14 ． ( 荆门中考 ) 二次函数 y ＝ ax 2 ＋ bx ＋ c(a≠0) 的大致图象如图所示，顶点坐标为 ( － 2 ，－ 9a) ，下列结论：① 4a ＋ 2b ＋ c>0 ；② 5a － b ＋ c ＝ 0 ；③若方程 a(x ＋ 5) · (x － 1) ＝－ 1 有两个根 x 1 和 x 2 ，且 x 1

查看更多