2019年四川省南充市中考数学试卷含答案

2019年四川省南充市中考数学试卷含答案

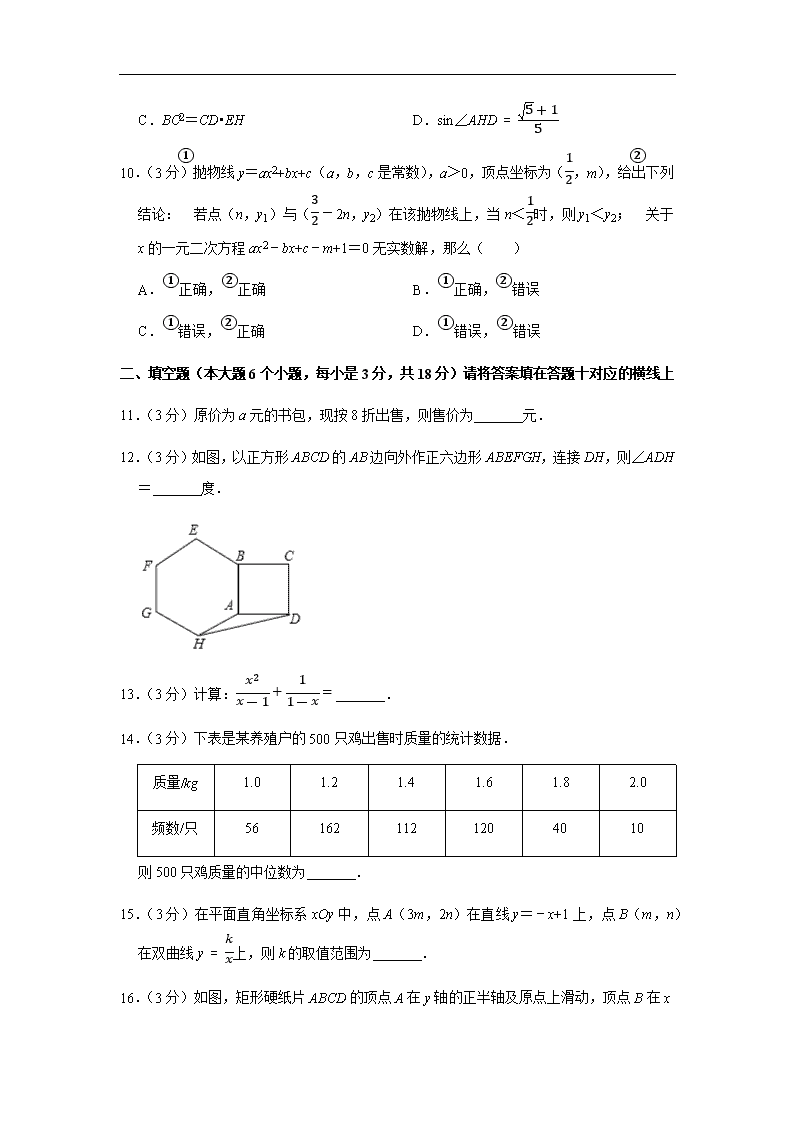
‎2019年四川省南充市中考数学试卷 一、选择题（本大题共10个小题，每小3分，共30分）每小题都有代号为A、B、C、D四个答案选项，其中只有一个是正确的，请根据正确选项的代号填涂答题卡对应位置，填涂正确记3分，不涂、填涂或多涂记0分．‎ ‎1．（3分）如果6a＝1，那么a的值为（　　）‎ A．6 B．‎1‎‎6‎ C．﹣6 D．‎‎-‎‎1‎‎6‎ ‎2．（3分）下列各式计算正确的是（　　）‎ A．x+x2＝x3 B．（x2）3＝x5 C．x6÷x2＝x3 D．x•x2＝x3‎ ‎3．（3分）如图是一个几何体的表面展开图，这个几何体是（　　）‎ A． B． C． D．‎ ‎4．（3分）在2019年南充市初中毕业升学体育与健康考试中，某校九年级（1）班体育委员对本班50名同学参加球类自选项目做了统计，制作出扇形统计图（如图），则该班选考乒乓球人数比羽毛球人数多（　　）‎ A．5人 B．10人 C．15人 D．20人 ‎5．（3分）如图，在△ABC中，AB的垂直平分线交AB于点D，交BC于点E，若BC＝6，AC＝5，则△ACE的周长为（　　）‎ A．8 B．11 C．16 D．17‎ ‎6．（3分）关于x的一元一次方程2xa﹣2+m＝4的解为x＝1，则a+m的值为（　　）‎ A．9 B．8 C．5 D．4‎ ‎7．（3分）如图，在半径为6的⊙O中，点A，B，C都在⊙O上，四边形OABC是平行四边形，则图中阴影部分的面积为（　　）‎ A．6π B．3‎3‎π C．2‎3‎π D．2π ‎8．（3分）关于x的不等式2x+a≤1只有2个正整数解，则a的取值范围为（　　）‎ A．﹣5＜a＜﹣3 B．﹣5≤a＜﹣3 C．﹣5＜a≤﹣3 D．﹣5≤a≤﹣3‎ ‎9．（3分）如图，正方形MNCB在宽为2的矩形纸片一端，对折正方形MNCB得到折痕AE，再翻折纸片，使AB与AD重合，以下结论错误的是（　　）‎ A．AB2＝10+2‎5‎ B．CDBC‎=‎‎5‎‎-1‎‎2‎ ‎ C．BC2＝CD•EH D．sin∠AHD‎=‎‎5‎‎+1‎‎5‎ ‎10．（3分）抛物线y＝ax2+bx+c（a，b，c是常数），a＞0，顶点坐标为（‎1‎‎2‎，m），给出下列结论：①若点（n，y1）与（‎3‎‎2‎‎-‎2n，y2）在该抛物线上，当n‎＜‎‎1‎‎2‎时，则y1＜y2；②关于x的一元二次方程ax2﹣bx+c﹣m+1＝0无实数解，那么（　　）‎ A．①正确，②正确 B．①正确，②错误 ‎ C．①错误，②正确 D．①错误，②错误 二、填空题（本大题6个小题，每小是3分，共18分）请将答案填在答题十对应的横线上 ‎11．（3分）原价为a元的书包，现按8折出售，则售价为　 　元．‎ ‎12．（3分）如图，以正方形ABCD的AB边向外作正六边形ABEFGH，连接DH，则∠ADH＝　 　度．‎ ‎13．（3分）计算：x‎2‎x-1‎‎+‎1‎‎1-x=‎　 　．‎ ‎14．（3分）下表是某养殖户的500只鸡出售时质量的统计数据．‎ 质量/kg ‎1.0‎ ‎1.2‎ ‎1.4‎ ‎1.6‎ ‎1.8‎ ‎2.0‎ 频数/只 ‎56‎ ‎162‎ ‎112‎ ‎120‎ ‎40‎ ‎10‎ 则500只鸡质量的中位数为　 　．‎ ‎15．（3分）在平面直角坐标系xOy中，点A（3m，2n）在直线y＝﹣x+1上，点B（m，n）在双曲线y‎=‎kx上，则k的取值范围为　 　．‎ ‎16．（3分）如图，矩形硬纸片ABCD的顶点A在y轴的正半轴及原点上滑动，顶点B在x 轴的正半轴及原点上滑动，点E为AB的中点，AB＝24，BC＝5．给出下列结论：①点A从点O出发，到点B运动至点O为止，点E经过的路径长为12π；②△OAB的面积最大值为144；③当OD最大时，点D的坐标为（‎25‎‎26‎‎26‎，‎125‎‎26‎‎26‎）．其中正确的结论是　 　．（填写序号）‎ 三、解答题（本大题共9个小题，共72分）解答应写出必要的文字说明，证明过程或演算步骤 ‎17．（6分）计算：（1﹣π）0+|‎2‎‎-‎‎3‎|‎-‎12‎+‎（‎1‎‎2‎）﹣1．‎ ‎18．（6分）如图，点O是线段AB的中点，OD∥BC且OD＝BC．‎ ‎（1）求证：△AOD≌△OBC；‎ ‎（2）若∠ADO＝35°，求∠DOC的度数．‎ ‎19．（6分）现有四张完全相同的不透明卡片，其正面分别写有数字﹣2，﹣1，0，2，把这四张卡片背面朝上洗匀后放在桌面上．‎ ‎（1）随机的取一张卡片，求抽取的卡片上的数字为负数的概率．‎ ‎（2）先随机抽取一张卡片，其上的数字作为点A的横坐标；然后放回并洗匀，再随机抽取一张卡片，其上的数字作为点A的纵坐标，试用画树状图或列表的方法求出点A 在直线y＝2x上的概率．‎ ‎20．（8分）已知关于x的一元二次方程x2+（2m﹣1）x+m2﹣3＝0有实数根．‎ ‎（1）求实数m的取值范围；‎ ‎（2）当m＝2时，方程的根为x1，x2，求代数式（x12+2x1）（x22+4x2+2）的值．‎ ‎21．（8分）双曲线y‎=‎kx（k为常数，且k≠0）与直线y＝﹣2x+b，交于A（‎-‎‎1‎‎2‎m，m﹣2），B（1，n）两点．‎ ‎（1）求k与b的值；‎ ‎（2）如图，直线AB交x轴于点C，交y轴于点D，若点E为CD的中点，求△BOE的面积．‎ ‎22．（8分）如图，在△ABC中，以AC为直径的⊙O交AB于点D，连接CD，∠BCD＝∠A．‎ ‎（1）求证：BC是⊙O的切线；‎ ‎（2）若BC＝5，BD＝3，求点O到CD的距离．‎ ‎23．（10分）在“我为祖国点赞“征文活动中，学校计划对获得一，二等奖的学生分别奖励一支钢笔，一本笔记本．已知购买2支钢笔和3个笔记本共38元，购买4支钢笔和5个笔记本共70元．‎ ‎（1）钢笔、笔记本的单价分别为多少元？‎ ‎（2）经与商家协商，购买钢笔超过30支时，每增加1支，单价降低0.1元；超过50支，均按购买50支的单价售，笔记本一律按原价销售．学校计划奖励一、二等奖学生共计100人，其中一等奖的人数不少于30人，且不超过60人，这次奖励一等奖学生多少人时，购买奖品总金额最少，最少为多少元？‎ ‎24．（10分）如图，在正方形ABCD中，点E是AB边上一点，以DE为边作正方形DEFG，DF与BC交于点M，延长EM交GF于点H，EF与CB交于点N，连接CG．‎ ‎（1）求证：CD⊥CG；‎ ‎（2）若tan∠MEN‎=‎‎1‎‎3‎，求MNEM的值；‎ ‎（3）已知正方形ABCD的边长为1，点E在运动过程中，EM的长能否为‎1‎‎2‎？请说明理由．‎ ‎25．（10分）如图，抛物线y＝ax2+bx+c与x轴交于点A（﹣1，0），点B（﹣3，0），且OB＝OC．‎ ‎（1）求抛物线的解析式；‎ ‎（2）点P在抛物线上，且∠POB＝∠ACB，求点P的坐标；‎ ‎（3）抛物线上两点M，N，点M的横坐标为m，点N的横坐标为m+4．点D是抛物线上M，N之间的动点，过点D作y轴的平行线交MN于点E．‎ ‎①求DE的最大值；‎ ‎②点D关于点E的对称点为F，当m为何值时，四边形MDNF为矩形．‎ ‎2019年四川省南充市中考数学试卷 参考答案与试题解析 一、选择题（本大题共10个小题，每小3分，共30分）每小题都有代号为A、B、C、D四个答案选项，其中只有一个是正确的，请根据正确选项的代号填涂答题卡对应位置，填涂正确记3分，不涂、填涂或多涂记0分．‎ ‎1．（3分）如果6a＝1，那么a的值为（　　）‎ A．6 B．‎1‎‎6‎ C．﹣6 D．‎‎-‎‎1‎‎6‎ ‎【解答】解：∵6a＝1，‎ ‎∴a‎=‎‎1‎‎6‎．‎ 故选：B．‎ ‎2．（3分）下列各式计算正确的是（　　）‎ A．x+x2＝x3 B．（x2）3＝x5 C．x6÷x2＝x3 D．x•x2＝x3‎ ‎【解答】解：A、x+x2，无法计算，故此选项错误；‎ B、（x2）3＝x6，故此选项错误；‎ C、x6÷x2＝x4，故此选项错误；‎ D、x•x2＝x3，故此选项正确；‎ 故选：D．‎ ‎3．（3分）如图是一个几何体的表面展开图，这个几何体是（　　）‎ A． B． C． D．‎ ‎【解答】解：由平面图形的折叠及三棱柱的展开图的特征可知，这个几何体是三棱柱．‎ 故选：C．‎ ‎4．（3分）在2019年南充市初中毕业升学体育与健康考试中，某校九年级（1）班体育委员对本班50名同学参加球类自选项目做了统计，制作出扇形统计图（如图），则该班选考乒乓球人数比羽毛球人数多（　　）‎ A．5人 B．10人 C．15人 D．20人 ‎【解答】解：∵选考乒乓球人数为50×40%＝20人，‎ 选考羽毛球人数为50‎×‎72°‎‎360°‎=‎10人，‎ ‎∴选考乒乓球人数比羽毛球人数多20﹣10＝10人，‎ 故选：B．‎ ‎5．（3分）如图，在△ABC中，AB的垂直平分线交AB于点D，交BC于点E，若BC＝6，AC＝5，则△ACE的周长为（　　）‎ A．8 B．11 C．16 D．17‎ ‎【解答】解：∵DE垂直平分AB，‎ ‎∴AE＝BE，‎ ‎∴△ACE的周长＝AC+CE+AE ‎＝AC+CE+BE ‎＝AC+BC ‎＝5+6‎ ‎＝11．‎ 故选：B．‎ ‎6．（3分）关于x的一元一次方程2xa﹣2+m＝4的解为x＝1，则a+m的值为（　　）‎ A．9 B．8 C．5 D．4‎ ‎【解答】解：因为关于x的一元一次方程2xa﹣2+m＝4的解为x＝1，‎ 可得：a﹣2＝1，2+m＝4，‎ 解得：a＝3，m＝2，‎ 所以a+m＝3+2＝5，‎ 故选：C．‎ ‎7．（3分）如图，在半径为6的⊙O中，点A，B，C都在⊙O上，四边形OABC是平行四边形，则图中阴影部分的面积为（　　）‎ A．6π B．3‎3‎π C．2‎3‎π D．2π ‎【解答】解：连接OB，‎ ‎∵四边形OABC是平行四边形，‎ ‎∴AB＝OC，‎ ‎∴AB＝OA＝OB，‎ ‎∴△AOB是等边三角形，‎ ‎∴∠AOB＝60°，‎ ‎∵OC∥AB，‎ ‎∴S△AOB＝S△ABC，‎ ‎∴图中阴影部分的面积＝S扇形AOB‎=‎60⋅π×36‎‎360‎=‎6π，‎ 故选：A．‎ ‎8．（3分）关于x的不等式2x+a≤1只有2个正整数解，则a的取值范围为（　　）‎ A．﹣5＜a＜﹣3 B．﹣5≤a＜﹣3 C．﹣5＜a≤﹣3 D．﹣5≤a≤﹣3‎ ‎【解答】解：解不等式2x+a≤1得：x‎≤‎‎1-a‎2‎，‎ 不等式有两个正整数解，一定是1和2，‎ 根据题意得：2‎≤‎1-a‎2‎＜‎3，‎ 解得：﹣5＜a≤﹣3．‎ 故选：C．‎ ‎9．（3分）如图，正方形MNCB在宽为2的矩形纸片一端，对折正方形MNCB得到折痕AE，再翻折纸片，使AB与AD重合，以下结论错误的是（　　）‎ A．AB2＝10+2‎5‎ B．CDBC‎=‎‎5‎‎-1‎‎2‎ ‎ C．BC2＝CD•EH D．sin∠AHD‎=‎‎5‎‎+1‎‎5‎ ‎【解答】解：在Rt△AEB中，AB‎=AE‎2‎+BE‎2‎=‎2‎‎2‎‎+‎‎1‎‎2‎=‎‎5‎，‎ ‎∵AB∥DH，BH∥AD，‎ ‎∴四边形ABHD是平行四边形，‎ ‎∵AB＝AD，‎ ‎∴四边形ABHD是菱形，‎ ‎∴AD＝AB‎=‎‎5‎，‎ ‎∴CD＝AD＝AD‎=‎5‎-‎1，‎ ‎∴CDBC‎=‎‎5‎‎-1‎‎2‎，故选项B正确，‎ ‎∵BC2＝4，CD•EH＝（‎5‎‎-‎1）（‎5‎‎+‎1）＝4，‎ ‎∴BC2＝CD•EH，故选项C正确，‎ ‎∵四边形ABHD是菱形，‎ ‎∴∠AHD＝∠AHB，‎ ‎∴sin∠AHD＝sin∠AHB‎=AEAH=‎2‎‎2‎‎2‎‎+(‎5‎+1‎‎)‎‎2‎=‎‎5‎‎+1‎‎5‎，故选项D正确，‎ 故选：A．‎ ‎10．（3分）抛物线y＝ax2+bx+c（a，b，c是常数），a＞0，顶点坐标为（‎1‎‎2‎，m ‎），给出下列结论：①若点（n，y1）与（‎3‎‎2‎‎-‎2n，y2）在该抛物线上，当n‎＜‎‎1‎‎2‎时，则y1＜y2；②关于x的一元二次方程ax2﹣bx+c﹣m+1＝0无实数解，那么（　　）‎ A．①正确，②正确 B．①正确，②错误 ‎ C．①错误，②正确 D．①错误，②错误 ‎【解答】解：①∵顶点坐标为（‎1‎‎2‎，m），n‎＜‎‎1‎‎2‎，‎ ‎∴点（n，y1）关于抛物线的对称轴x‎=‎‎1‎‎2‎的对称点为（1﹣n，y1），‎ ‎∴点（1﹣n，y1）与（‎3‎‎2‎‎-‎2n，y2）在该抛物线上，‎ ‎∵（1﹣n）﹣（‎3‎‎2‎‎-‎2n）＝n‎-‎1‎‎2‎＜‎0，‎ ‎∴1﹣n‎＜‎3‎‎2‎-‎2n，‎ ‎∵a＞0，‎ ‎∴当x‎＞‎‎1‎‎2‎时，y随x的增大而增大，‎ ‎∴y1＜y2，故此小题结论正确；‎ ‎②把（‎1‎‎2‎，m）代入y＝ax2+bx+c中，得m‎=‎‎1‎‎4‎a‎+‎‎1‎‎2‎b+c，‎ ‎∴一元二次方程ax2﹣bx+c﹣m+1＝0中，△＝b2﹣4ac+4am﹣4a＝b2﹣4ac+4a（‎1‎‎4‎a‎+‎‎1‎‎2‎b+c）﹣4a＝（a+b）2﹣4a＜0，‎ ‎∴一元二次方程ax2﹣bx+c﹣m+1＝0无实数解，故此小题正确；‎ 故选：A．‎ 二、填空题（本大题6个小题，每小是3分，共18分）请将答案填在答题十对应的横线上 ‎11．（3分）原价为a元的书包，现按8折出售，则售价为　‎4‎‎5‎a　元．‎ ‎【解答】解：依题意可得，‎ 售价为‎8‎‎10‎a=‎‎4‎‎5‎a，‎ 故答案为‎4‎‎5‎a．‎ ‎12．（3分）如图，以正方形ABCD的AB边向外作正六边形ABEFGH，连接DH，则∠ADH＝　15　度．‎ ‎【解答】解：∵四边形ABCD 是正方形，‎ ‎∴AB＝AD，∠BAD＝90°，‎ 在正六边形ABEFGH中，∵AB＝AH，∠BAH＝120°，‎ ‎∴AH＝AD，∠HAD＝360°﹣90°﹣120°＝150°，‎ ‎∴∠ADH＝∠AHD‎=‎‎1‎‎2‎（180°﹣150°）＝15°，‎ 故答案为：15．‎ ‎13．（3分）计算：x‎2‎x-1‎‎+‎1‎‎1-x=‎　x+1　．‎ ‎【解答】解：原式‎=x‎2‎x-1‎-‎1‎x-1‎=‎(x+1)(x-1)‎x-1‎=‎x+1．‎ 故答案为：x+1‎ ‎14．（3分）下表是某养殖户的500只鸡出售时质量的统计数据．‎ 质量/kg ‎1.0‎ ‎1.2‎ ‎1.4‎ ‎1.6‎ ‎1.8‎ ‎2.0‎ 频数/只 ‎56‎ ‎162‎ ‎112‎ ‎120‎ ‎40‎ ‎10‎ 则500只鸡质量的中位数为　1.4kg　．‎ ‎【解答】解：500个数据的中位数是第250、251个数据的平均数，‎ ‎∵第250和251个数据分别为1.4、1.4，‎ ‎∴这组数据的中位数为‎1.4+1.4‎‎2‎‎=‎1.4（kg），‎ 故答案为：1.4kg．‎ ‎15．（3分）在平面直角坐标系xOy中，点A（3m，2n）在直线y＝﹣x+1上，点B（m，n）在双曲线y‎=‎kx上，则k的取值范围为　k‎≤‎‎1‎‎24‎且k≠0　．‎ ‎【解答】解：∵点A（3m，2n）在直线y＝﹣x+1上，‎ ‎∴2n＝﹣3m+1，即n‎=‎‎-3m+1‎‎2‎，‎ ‎∴B（m，‎-3m+1‎‎2‎），‎ ‎∵点B在双曲线y‎=‎kx上，‎ ‎∴k＝m•‎-3m+1‎‎2‎‎=-‎‎3‎‎2‎（m‎-‎‎1‎‎6‎）2‎+‎‎1‎‎24‎，‎ ‎∵‎-‎3‎‎2‎＜‎0，‎ ‎∴k有最大值为‎1‎‎24‎，‎ ‎∴k的取值范围为k‎≤‎‎1‎‎24‎，‎ ‎∵k≠0，‎ 故答案为k‎≤‎‎1‎‎24‎且k≠0．‎ ‎16．（3分）如图，矩形硬纸片ABCD的顶点A在y轴的正半轴及原点上滑动，顶点B在x轴的正半轴及原点上滑动，点E为AB的中点，AB＝24，BC＝5．给出下列结论：①点A从点O出发，到点B运动至点O为止，点E经过的路径长为12π；②△OAB的面积最大值为144；③当OD最大时，点D的坐标为（‎25‎‎26‎‎26‎，‎125‎‎26‎‎26‎）．其中正确的结论是　②③　．（填写序号）‎ ‎【解答】解：∵点E为AB的中点，AB＝24，‎ ‎∴OE‎=‎1‎‎2‎AB=12‎，‎ ‎∴AB的中点E的运动轨迹是以点O为圆心，12为半径的一段圆弧，‎ ‎∵∠AOB＝90°，‎ ‎∴点E经过的路径长为‎90×12×π‎180‎‎=6π，故①错误；‎ 当△OAB的面积最大时，因为AB＝24，所以△OAB为等腰直角三角形，即OA＝OB，‎ ‎∵E为AB的中点，‎ ‎∴OE⊥AB，OE‎=‎1‎‎2‎AB=12‎，‎ ‎∴S‎△AOB‎=‎1‎‎2‎×24×12=‎144，故②正确；‎ 如图，当O、E、D三点共线时，OD最大，过点D作DF⊥y轴于点F，‎ ‎∵AD＝BC＝5，AE‎=‎1‎‎2‎AB=12‎，‎ ‎∴DE=AD‎2‎+AE‎2‎=‎5‎‎2‎‎+1‎‎2‎‎2‎=‎13，‎ ‎∴OD＝DE+OE＝13+12＝25，‎ 设DF＝x，‎ ‎∴OF=OD‎2‎-DF‎2‎=‎‎2‎5‎‎2‎-‎x‎2‎，‎ ‎∵四边形ABCD是矩形，‎ ‎∴∠DAB＝90°，‎ ‎∴∠DFA＝∠AOB，‎ ‎∴∠DAF＝∠ABO，‎ ‎∴△DFA∽△AOB ‎∴DFOA‎=‎DAAB，‎ ‎∴xOA‎=‎‎5‎‎24‎，‎ ‎∴OA=‎‎24x‎5‎，‎ ‎∵E为AB的中点，∠AOB＝90°，‎ ‎∴AE＝OE，‎ ‎∴∠AOE＝∠OAE，‎ ‎∴△DFO∽△BOA，‎ ‎∴ODAB‎=‎OFOA，‎ ‎∴‎25‎‎24‎‎=‎‎2‎5‎‎2‎-‎x‎2‎‎24x‎5‎，‎ 解得x‎=‎‎25‎‎26‎‎26‎，x‎=-‎‎25‎‎26‎‎26‎舍去，‎ ‎∴OF=‎‎125‎‎26‎‎26‎，‎ ‎∴D(‎25‎‎26‎‎26‎，‎125‎‎26‎‎26‎)‎．故③正确．‎ 故答案为：②③．‎ 三、解答题（本大题共9个小题，共72分）解答应写出必要的文字说明，证明过程或演算步骤 ‎17．（6分）计算：（1﹣π）0+|‎2‎‎-‎‎3‎|‎-‎12‎+‎（‎1‎‎2‎）﹣1．‎ ‎【解答】解：原式＝1‎+‎3‎-‎2‎-2‎3‎+‎2‎=1-‎‎3‎．‎ ‎18．（6分）如图，点O是线段AB的中点，OD∥BC且OD＝BC．‎ ‎（1）求证：△AOD≌△OBC；‎ ‎（2）若∠ADO＝35°，求∠DOC的度数．‎ ‎【解答】（1）证明：∵点O是线段AB的中点，‎ ‎∴AO＝BO，‎ ‎∵OD∥BC，‎ ‎∴∠AOD＝∠OBC，‎ 在△AOD与△OBC中，AO=BO‎∠AOD=∠OBCOD=BC，‎ ‎∴△AOD≌△OBC（SAS）；‎ ‎（2）解：∵△AOD≌△OBC，‎ ‎∴∠ADO＝∠OCB＝35°，‎ ‎∵OD∥BC，‎ ‎∴∠DOC＝∠OCB＝35°．‎ ‎19．（6分）现有四张完全相同的不透明卡片，其正面分别写有数字﹣2，﹣1，0，2，把这四张卡片背面朝上洗匀后放在桌面上．‎ ‎（1）随机的取一张卡片，求抽取的卡片上的数字为负数的概率．‎ ‎（2）先随机抽取一张卡片，其上的数字作为点A的横坐标；然后放回并洗匀，再随机抽取一张卡片，其上的数字作为点A的纵坐标，试用画树状图或列表的方法求出点A在直线y＝2x上的概率．‎ ‎【解答】解：（1）随机的取一张卡片，抽取的卡片上的数字为负数的概率为‎2‎‎4‎‎=‎‎1‎‎2‎；‎ ‎（2）画树状图如图所示：‎ 共有16个可能的结果，点A在直线y＝2x上的结果有2个，‎ ‎∴点A在直线y＝2x上的概率为‎2‎‎16‎‎=‎‎1‎‎8‎．‎ ‎20．（8分）已知关于x的一元二次方程x2+（2m﹣1）x+m2﹣3＝0有实数根．‎ ‎（1）求实数m的取值范围；‎ ‎（2）当m＝2时，方程的根为x1，x2，求代数式（x12+2x1）（x22+4x2+2）的值．‎ ‎【解答】解：（1）由题意△≥0，‎ ‎∴（2m﹣1）2﹣4（m2﹣3）≥0，‎ ‎∴m‎≤‎‎13‎‎4‎．‎ ‎（2）当m＝2时，方程为x2+3x+1＝0，‎ ‎∴x1+x2＝﹣3，x1x2＝1，‎ ‎∵方程的根为x1，x2，‎ ‎∴x12+3x1+1＝0，x22+3x2+1＝0，‎ ‎∴（x12+2x1）（x22+4x2+2）‎ ‎＝（x12+2x1+x1﹣x1）（x22+3x2+x2+2）‎ ‎＝（﹣1﹣x1）（﹣1+x2+2）‎ ‎＝（﹣1﹣x1）（x2+1）‎ ‎＝﹣x2﹣x1x2﹣1﹣x1‎ ‎＝﹣x2﹣x1﹣2‎ ‎＝3﹣2‎ ‎＝1．‎ ‎21．（8分）双曲线y‎=‎kx（k为常数，且k≠0）与直线y＝﹣2x+b，交于A（‎-‎‎1‎‎2‎m，m﹣2），B（1，n）两点．‎ ‎（1）求k与b的值；‎ ‎（2）如图，直线AB交x轴于点C，交y轴于点D，若点E为CD的中点，求△BOE的面积．‎ ‎【解答】解：（1）∵点A（‎-‎‎1‎‎2‎m，m﹣2），B（1，n）在直线y＝﹣2x+b上，‎ ‎∴m+b=m-2‎‎-2+b=n，‎ 解得：b=-2‎n=-4‎，‎ ‎∴B（1，﹣4），‎ 代入反比例函数解析式y=‎kx，‎ ‎∴﹣4‎=‎k‎1‎，‎ ‎∴k＝﹣4．‎ ‎（2）∵直线AB的解析式为y＝﹣2x﹣2，‎ 令x＝0，解得y＝﹣2，令y＝0，解得x＝﹣1，‎ ‎∴C（﹣1，0），D（0，﹣2），‎ ‎∵点E为CD的中点，‎ ‎∴E（‎-‎1‎‎2‎，-1‎），‎ ‎∴S△BOE＝S△ODE+S△ODB‎=‎1‎‎2‎OD⋅(xB-xE)=‎1‎‎2‎×2×(1+‎1‎‎2‎)‎ ‎=‎‎3‎‎2‎‎．‎ ‎22．（8分）如图，在△ABC中，以AC为直径的⊙O交AB于点D，连接CD，∠BCD＝∠A．‎ ‎（1）求证：BC是⊙O的切线；‎ ‎（2）若BC＝5，BD＝3，求点O到CD的距离．‎ ‎【解答】（1）证明：∵AC是⊙O的直径，‎ ‎∴∠ADC＝90°，‎ ‎∴∠A+∠ACD＝90°，‎ ‎∵∠BCD＝∠A，‎ ‎∴∠ACD+∠BCD＝90°，‎ ‎∴∠ACB＝90°，‎ ‎∴BC是⊙O的切线；‎ ‎（2）解：过O作OH⊥CD于H，‎ ‎∵∠BDC＝∠ACB＝90°，∠B＝∠B，‎ ‎∴△ACB∽△CDB，‎ ‎∴BCBD‎=‎ABBC，‎ ‎∴‎5‎‎3‎‎=‎AB‎5‎，‎ ‎∴AB‎=‎‎25‎‎3‎，‎ ‎∴AD‎=‎‎16‎‎3‎，‎ ‎∵OH⊥CD，‎ ‎∴CH＝DH，‎ ‎∵AO＝OC，‎ ‎∴OH‎=‎‎1‎‎2‎AD‎=‎‎8‎‎3‎，‎ ‎∴点O到CD的距离是‎8‎‎3‎．‎ ‎23．（10分）在“我为祖国点赞“征文活动中，学校计划对获得一，二等奖的学生分别奖励一支钢笔，一本笔记本．已知购买2支钢笔和3个笔记本共38元，购买4支钢笔和5个笔记本共70元．‎ ‎（1）钢笔、笔记本的单价分别为多少元？‎ ‎（2）经与商家协商，购买钢笔超过30支时，每增加1支，单价降低0.1元；超过50支，均按购买50支的单价售，笔记本一律按原价销售．学校计划奖励一、二等奖学生共计100人，其中一等奖的人数不少于30人，且不超过60人，这次奖励一等奖学生多少人时，购买奖品总金额最少，最少为多少元？‎ ‎【解答】解：（1）钢笔、笔记本的单价分别为x、y元，‎ 根据题意得，‎2x+3y=38‎‎4x+5y=70‎，‎ 解得：x=10‎y=6‎，‎ 答：钢笔、笔记本的单价分别为10元，6元；‎ ‎（2）设钢笔的单价为a元，购买数量为b元，支付钢笔和笔记本的总金额w元，‎ ‎①当30≤b≤50时，a＝10﹣0.1（b﹣30）＝﹣0.1b+13，w＝b（﹣0.1b+13）+6（100﹣b）＝﹣0.1b2+7b+600＝﹣0.1（b﹣35）2+722.5，‎ ‎∵当b＝30时，w＝720，当b＝50时，w＝700，‎ ‎∴当30≤b≤50时，700≤w≤722.5；‎ ‎②当50＜b≤60时，a＝8，w＝8b+6（100﹣b）＝2b+600，‎ ‎700＜w≤720，‎ ‎∴当30≤b≤60时，w的最小值为700元，‎ ‎∴这次奖励一等奖学生50人时，购买奖品总金额最少，最少为700元．‎ ‎24．（10分）如图，在正方形ABCD中，点E是AB边上一点，以DE为边作正方形DEFG，DF与BC交于点M，延长EM交GF于点H，EF与CB交于点N，连接CG．‎ ‎（1）求证：CD⊥CG；‎ ‎（2）若tan∠MEN‎=‎‎1‎‎3‎，求MNEM的值；‎ ‎（3）已知正方形ABCD的边长为1，点E在运动过程中，EM的长能否为‎1‎‎2‎？请说明理由．‎ ‎【解答】（1）证明：∵四边形ABCD和四边形DEFG是正方形，‎ ‎∴∠A＝∠ADC＝∠EDG＝90°，AD＝CD，DE＝DG，‎ ‎∴∠ADE＝∠CDG，‎ 在△ADE和△CDG中，AD=CD‎∠ADE=∠CDGDE=DG，‎ ‎∴△ADE≌△CDG（SAS），‎ ‎∴∠A＝∠DCG＝90°，‎ ‎∴CD⊥CG；‎ ‎（2）解：∵四边形DEFG是正方形，‎ ‎∴EF＝GF，∠EFM＝∠GFM＝45°，‎ 在△EFM和△GFM中EF=GF‎∠EFM=∠GFMMF=MF，‎ ‎∴△EFM≌△GFM（SAS），‎ ‎∴EM＝GM，∠MEF＝∠MGF，‎ 在△EFH和△GFN中，‎∠EFH=∠GFNEF=GF‎∠MEF=∠MGF，‎ ‎∴△EFH≌△GFN（ASA），‎ ‎∴HF＝NF，‎ ‎∵tan∠MEN‎=‎1‎‎3‎=‎HFEF，‎ ‎∴GF＝EF＝3HF＝3NF，‎ ‎∴GH＝2HF，‎ 作NP∥GF交EM于P，则△PMN∽△HMG，△PEN∽△HEF，‎ ‎∴PNGH‎=‎MNGM，PNHF‎=ENEF=‎‎2‎‎3‎，‎ ‎∴PN‎=‎‎2‎‎3‎HF，‎ ‎∴MNEM‎=MNGM=PNGH=‎2‎‎3‎HF‎2HF=‎‎1‎‎3‎；‎ ‎（3）EM的长不可能为‎1‎‎2‎，‎ 理由：假设EM的长为‎1‎‎2‎，‎ ‎∵点E是AB边上一点，且∠EDG＝∠ADC＝90°，‎ ‎∴点G在BC的延长线上，‎ 同（2）的方法得，EM＝GM‎=‎‎1‎‎2‎，‎ ‎∴GM‎=‎‎1‎‎2‎，‎ 在Rt△BEM中，EM是斜边，‎ ‎∴BM‎＜‎‎1‎‎2‎，‎ ‎∵正方形ABCD的边长为1，‎ ‎∴BC＝1，‎ ‎∴CM‎＞‎‎1‎‎2‎，‎ ‎∴CM＞GM，‎ ‎∴点G在正方形ABCD的边BC上，与“点G在BC的延长线上”相矛盾，‎ ‎∴假设错误，‎ 即：EM的长不可能为‎1‎‎2‎．‎ ‎25．（10分）如图，抛物线y＝ax2+bx+c与x轴交于点A（﹣1，0），点B（﹣3，0），且OB＝OC．‎ ‎（1）求抛物线的解析式；‎ ‎（2）点P在抛物线上，且∠POB＝∠ACB，求点P的坐标；‎ ‎（3）抛物线上两点M，N，点M的横坐标为m，点N的横坐标为m+4．点D是抛物线上M，N之间的动点，过点D作y轴的平行线交MN于点E．‎ ‎①求DE的最大值；‎ ‎②点D关于点E的对称点为F，当m为何值时，四边形MDNF为矩形．‎ ‎【解答】解：（1）∵抛物线与x轴交于点A（﹣1，0），点B（﹣3，0）‎ ‎∴设交点式y＝a（x+1）（x+3）‎ ‎∵OC＝OB＝3，点C在y轴负半轴 ‎∴C（0，﹣3）‎ 把点C代入抛物线解析式得：3a＝﹣3‎ ‎∴a＝﹣1‎ ‎∴抛物线解析式为y＝﹣（x+1）（x+3）＝﹣x2﹣4x﹣3‎ ‎（2）如图1，过点A作AG⊥BC于点G，过点P作PH⊥x轴于点H ‎∴∠AGB＝∠AGC＝∠PHO＝90°‎ ‎∵∠ACB＝∠POB ‎∴△ACG∽△POH ‎∴‎AGPH‎=‎CGOH ‎∴‎AGCG‎=‎PHOH ‎∵OB＝OC＝3，∠BOC＝90°‎ ‎∴∠ABC＝45°，BC‎=OB‎2‎+OC‎2‎=‎3‎‎2‎ ‎∴△ABG是等腰直角三角形 ‎∴AG＝BG‎=‎‎2‎‎2‎AB‎=‎‎2‎ ‎∴CG＝BC﹣BG＝3‎2‎‎-‎2‎=‎2‎‎2‎ ‎∴‎PHOH‎=AGCG=‎‎1‎‎2‎ ‎∴OH＝2PH 设P（p，﹣p2﹣4p﹣3）‎ ‎①当p＜﹣3或﹣1＜p＜0时，点P在点B左侧或在AC之间，横纵坐标均为负数 ‎∴OH＝﹣p，PH＝﹣（﹣p2﹣4p﹣3）＝p2+4p+3‎ ‎∴﹣p＝2（p2+4p+3）‎ 解得：p1‎=‎‎-9-‎‎33‎‎4‎，p2‎‎=‎‎-9+‎‎33‎‎4‎ ‎∴P（‎-9-‎‎33‎‎4‎，‎-9-‎‎33‎‎8‎）或（‎-9+‎‎33‎‎4‎，‎-9+‎‎33‎‎8‎）‎ ‎②当﹣3＜p＜﹣1或p＞0时，点P在AB之间或在点C右侧，横纵坐标异号 ‎∴p＝2（p2+4p+3）‎ 解得：p1＝﹣2，p2‎‎=-‎‎3‎‎2‎ ‎∴P（﹣2，1）或（‎-‎‎3‎‎2‎，‎3‎‎4‎）‎ 综上所述，点P的坐标为（‎-9-‎‎33‎‎4‎，‎-9-‎‎33‎‎8‎）、（‎-9+‎‎33‎‎4‎，‎-9+‎‎33‎‎8‎）、（﹣2，1）或（‎-‎‎3‎‎2‎，‎3‎‎4‎）．‎ ‎（3）①如图2，∵x＝m+4时，y＝﹣（m+4）2﹣4（m+4）﹣3＝﹣m2﹣12m﹣35‎ ‎∴M（m，﹣m2﹣4m﹣3），N（m+4，﹣m2﹣12m﹣35）‎ 设直线MN解析式为y＝kx+n ‎∴km+n=-m‎2‎-4m-3‎k(m+4)+n=-m‎2‎-12m-35‎ 解得：‎k=-2m-8‎n=m‎2‎+4m-3‎ ‎∴直线MN：y＝（﹣2m﹣8）x+m2+4m﹣3‎ 设D（d，﹣d2﹣4d﹣3）（m＜d＜m+4）‎ ‎∵DE∥y轴 ‎∴xE＝xD＝d，E（d，（﹣2m﹣8）d+m2+4m﹣3）‎ ‎∴DE＝﹣d2﹣4d﹣3﹣[（﹣2m﹣8）d+m2+4m﹣3]＝﹣d2+（2m+4）d﹣m2﹣4m＝﹣[d﹣（m+2）]2+4‎ ‎∴当d＝m+2时，DE的最大值为4．‎ ‎②如图3，∵D、F关于点E对称 ‎∴DE＝EF ‎∵四边形MDNF是矩形 ‎∴MN＝DF，且MN与DF互相平分 ‎∴DE‎=‎‎1‎‎2‎MN，E为MN中点 ‎∴xD＝xE‎=m+m+4‎‎2‎=‎m+2‎ 由①得当d＝m+2时，DE＝4‎ ‎∴MN＝2DE＝8‎ ‎∴（m+4﹣m）2+[﹣m2﹣12m﹣35﹣（﹣m2﹣4m﹣3）]2＝82‎ 解得：m1＝﹣4‎-‎‎3‎‎2‎，m2＝﹣4‎‎+‎‎3‎‎2‎ ‎∴m的值为﹣4‎-‎‎3‎‎2‎或﹣4‎+‎‎3‎‎2‎时，四边形MDNF为矩形．‎ 声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布 日期：2019/6/30 9:58:00；用户：中考培优辅导；邮箱：p5193@xyh.com；学号：27411521‎