2009年辽宁省铁岭市中考数学试题（含答案）

2009年辽宁省铁岭市中考数学试题（含答案）

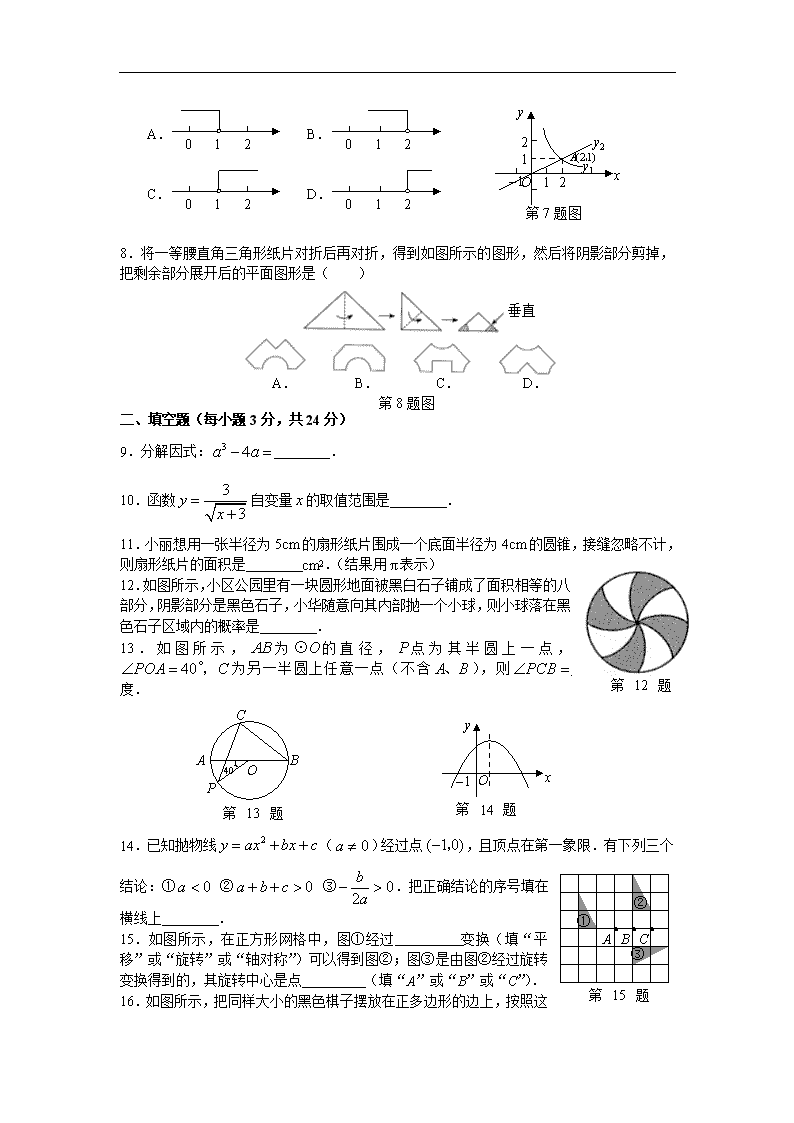
‎2009年铁岭市初中毕业生学业考试 数 学 试 卷 ‎※考试时间120分钟 试卷满分150分 一、选择题（下列各题的备选答案中，只有一个是正确的，请将正确答案的选项填在下表中相应题号下的空格内．每小题3分，共24分）‎ ‎1．目前国内规划中的第一高楼上海中心大厦，总投入约14 800 000 000元．14 800 000 000元用科学记数法表示为（ ）‎ A．元 B．元 C．元 D．元 ‎2．计算的结果为（ ）‎ E A B C D 第3题图 ‎45°‎ ‎125°‎ A． B． C． D．‎ ‎3．如图所示，已知直线，，，‎ 则的度数为（ ）‎ A．70 B．80 ‎ C．90 D．100‎ ‎4．一个圆柱体钢块，正中央被挖去了一个长方体孔，其俯视图如图所示，则此圆柱体钢块的左视图是（ ）‎ A．‎ B．‎ C．‎ D．‎ 俯视图 第4题图 ‎5．数据21，21，21，25，26，27的众数、中位数分别是（ ）‎ A．21，23 B．21，‎21 ‎ C．23，21 D．21，25‎ ‎6．为了美化环境，某市加大对绿化的投资．2007年用于绿化投资20万元，2009年用于绿化投资25万元，求这两年绿化投资的年平均增长率．设这两年绿化投资的年平均增长率为，根据题意所列方程为（ ）‎ A． B．‎ C． D．‎ ‎7．如图所示，反比例函数与正比例函数的图象的一个交点坐标是，若，则的取值范围在数轴上表示为（ ）‎ y ‎1‎ ‎2‎ ‎2‎ ‎1‎ y2‎ y1‎ x O 第7题图 ‎1‎ ‎2‎ ‎0‎ A．‎ ‎1‎ ‎2‎ ‎0‎ B．‎ ‎1‎ ‎2‎ ‎0‎ C．‎ ‎1‎ ‎2‎ ‎0‎ D．‎ ‎8．将一等腰直角三角形纸片对折后再对折，得到如图所示的图形，然后将阴影部分剪掉，把剩余部分展开后的平面图形是（ ）‎ 垂直 A．‎ B．‎ C．‎ D．‎ 第8题图 二、填空题（每小题3分，共24分）‎ ‎9．分解因式： ．‎ ‎10．函数自变量的取值范围是 ．‎ 第12题图 ‎11．小丽想用一张半径为‎5cm的扇形纸片围成一个底面半径为‎4cm的圆锥，接缝忽略不计，则扇形纸片的面积是 cm2．（结果用表示）‎ ‎12．如图所示，小区公园里有一块圆形地面被黑白石子铺成了面积相等的八部分，阴影部分是黑色石子，小华随意向其内部抛一个小球，则小球落在黑色石子区域内的概率是 ．‎ ‎13．如图所示，为的直径，点为其半圆上一点，为另一半圆上任意一点（不含），则 度．‎ C B A P O ‎40°‎ 第13题图 O y x 第14题图 ‎①‎ ‎②‎ ‎③‎ 第15题图 A B C ‎14．已知抛物线（）经过点，且顶点在第一象限．有下列三个结论：① ② ③．把正确结论的序号填在横线上 ．‎ ‎15．如图所示，在正方形网格中，图①经过 变换（填“平移”或“旋转”或“轴对称”）可以得到图②；图③是由图②经过旋转变换得到的，其旋转中心是点 （填“A”或“B”或“C”）．‎ ‎16．如图所示，把同样大小的黑色棋子摆放在正多边形的边上，按照这样的规律摆下去，则第个图形需要黑色棋子的个数是 ．‎ 第1个图形 第2个图形 第3个图形 第4个图形 第16题图 三、解答题（每题8分，共16分）‎ ‎17．计算：．‎ ‎18．解方程：．‎ 四、解答题（每题10分，共20分）‎ ‎19．如图所示，在中，．‎ ‎（1）尺规作图：作线段的垂直平分线（保留作图痕迹，不写作法）；‎ ‎（2）在已作的图形中，若分别交及的延长线于点，连接．‎ A C B 第19题图 求证：．‎ ‎20．某市开展了党员干部“一帮一扶贫”活动．为了解贫困群众对帮扶情况的满意程度，有关部门在该市所管辖的两个区内，分别随机抽取了若干名贫困群众进行问卷调查．根据收集的信息进行了统计，并绘制了下面尚不完整的统计图．已知在甲区所调查的贫困群众中，非常满意的人数占甲区所调查的总人数的35%．根据统计图所提供的信息解答下列问题：‎ ‎（1）甲区参加问卷调查的贫困群众有 人；‎ ‎（2）请将统计图补充完整；‎ 非常满意 人数 ‎800‎ ‎600‎ ‎400‎ ‎200‎ 满意 比较满意 不满意 满意程度 甲 乙 第20题图 ‎420‎ ‎700‎ ‎760‎ ‎500‎ ‎250‎ ‎30‎ ‎40‎ ‎（3）小红说：“因为甲区有30人不满意，乙区有40人不满意，所以甲区的不满意率比乙区低．”你认为这种说法正确吗？为什么？‎ 五、解答题（每题10分，共20分）‎ ‎21．小明和小亮是一对双胞胎，他们的爸爸买了两套不同品牌的运动服送给他们，小明和小亮都想先挑选．于是小明设计了如下游戏来决定谁先挑选．游戏规则是：在一个不透明的袋子里装有除数字以外其它均相同的4个小球，上面分别标有数字1、2、3、4．一人先从袋中随机摸出一个小球，另一人再从袋中剩下的3个小球中随机摸出一个小球．若摸出的两个小球上的数字和为奇数，则小明先挑选；否则小亮先挑选．‎ ‎（1）用树状图或列表法求出小明先挑选的概率；‎ ‎（2）你认为这个游戏公平吗？请说明理由．‎ ‎22．如图所示，已知是半圆的直径，弦，是延长线上一点，．判断直线与半圆的位置关系，并证明你的结论．‎ O A B E D C 第22题图 六、解答题（每题10分，共20分）‎ ‎23．某旅游区有一个景观奇异的望天洞，点是洞的入口，游人从入口进洞游览后，可经山洞到达山顶的出口凉亭处观看旅游区风景，最后坐缆车沿索道返回山脚下的处．在同一平面内，若测得斜坡的长为‎100米，坡角，在处测得的仰角，在处测得的仰角，过点作地面的垂线，垂足为．‎ ‎（1）求的度数；‎ A C D E F B 第23题图 ‎（2）求索道的长．（结果保留根号）‎ 一等奖 二等奖 三等奖 单价(元)‎ ‎12‎ ‎10‎ ‎5‎ ‎24．为迎接国庆六十周年，某校团委组织了“歌唱祖国”有奖征文活动，并设立了一、二、三等奖．学校计划派人根据设奖情况买50件奖品，其中二等奖件数比一等奖件数的2倍还少10件，三等奖所花钱数不超过二等奖所花钱数的1.5倍．各种奖品的单价如下表所示．如果计划一等奖买件，买50件奖品的总钱数是元．‎ ‎（1）求与的函数关系式及自变量的取值范围；‎ ‎（2）请你计算一下，如果购买这三种奖品所花的总钱数最少？最少是多少元？‎ 七、解答题（本题12分）‎ ‎25．是等边三角形，点是射线上的一个动点（点不与点重合），是以为边的等边三角形，过点作的平行线，分别交射线于点，连接．‎ ‎（1）如图（a）所示，当点在线段上时．‎ ‎ ①求证：；‎ ‎②探究四边形是怎样特殊的四边形？并说明理由；‎ ‎（2）如图（b）所示，当点在的延长线上时，直接写出（1）中的两个结论是否成立？‎ ‎（3）在（2）的情况下，当点运动到什么位置时，四边形是菱形？并说明理由．‎ A G C D B F E 图（a）‎ A D C B F E G 图（b）‎ 第25题图 八、解答题（本题14分）‎ ‎26．如图所示，已知在直角梯形中，轴于点．动点从点出发，沿轴正方向以每秒1个单位长度的速度移动．过点作垂直于直线，垂足为．设点移动的时间为秒（），与直角梯形重叠部分的面积为．‎ ‎（1）求经过三点的抛物线解析式；‎ ‎（2）求与的函数关系式；‎ ‎（3）将绕着点顺时针旋转，是否存在，使得的顶点或在抛物线上？若存在，直接写出的值；若不存在，请说明理由．‎ ‎2‎ O A B C x y ‎1‎ ‎1‎ ‎3‎ P 第26题图 Q ‎2009年铁岭市初中毕业生学业考试 数学试题参考答案及评分标准 注：本参考答案只给出一种或几种解法（证法），若用其他方法解答并正确，可参考此评分标准相应步骤赋分．‎ 一、选择题（每小题3分，共24分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 答案 C B B C A C D A 二、填空题（每小题3分，共24分）‎ ‎9． 10． 11． 12． 13．70‎ ‎14．①②③ 15．平移（2分）；A（3分） 16．或或 三、（每题8分，共16分）‎ ‎17．解：原式 6分 ‎ 8分 ‎18．解：方程两边分别乘以得 ‎ 3分 ‎ 7分 检验：当时，（或分母不等于0）‎ ‎∴是原方程的根． 8分 四、（每题10分，共20分）‎ A C B 第19题图 F E D l ‎19．（1）直线即为所求． 1分 作图正确． 3分 ‎（2）证明：在中，‎ 又∵为线段的垂直平分线，‎ ‎∴， 5分 ‎∴，‎ ‎∴．‎ 又∵，‎ ‎∴． 8分 在中，，‎ ‎∴，‎ ‎∴． 10分 ‎20．（1）1200 3分 ‎（2）图形正确（甲区满意人数有500人） 5分 ‎（3）不正确． 6分 ‎∵甲区的不满意率是，乙区的不满意率是，‎ ‎∴甲区的不满意率比乙区的不满意率高． 10分 五、（每题10分，共20分）‎ ‎21．解：（1）根据题意可列表或树状图如下：‎ ‎ 第一次 第二次 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎1‎ ‎——‎ ‎（1，2）‎ ‎（1，3）‎ ‎（1，4）‎ ‎2‎ ‎（2，1）‎ ‎——‎ ‎（2，3）‎ ‎（2，4）‎ ‎3‎ ‎（3，1）‎ ‎（3，2）‎ ‎——‎ ‎（3，4）‎ ‎4‎ ‎（4，1）‎ ‎（4，2）‎ ‎（4，3）‎ ‎——‎ ‎ 5分 ‎（1，2）‎ ‎（1，3）‎ ‎（1，4）‎ ‎2‎ ‎3‎ ‎4‎ ‎1‎ ‎（1，1）‎ ‎（2，3）‎ ‎（2，4）‎ ‎1‎ ‎3‎ ‎4‎ ‎2‎ ‎（3，1）‎ ‎（3，2）‎ ‎（3，4）‎ ‎1‎ ‎2‎ ‎4‎ ‎3‎ ‎（4，1）‎ ‎（4，2）‎ ‎（4，3）‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ 第一次摸球 第二次摸球 ‎ 5分 从表或树状图可以看出所有可能结果共有12种，且每种结果发生的可能性相同，符合条件的结果有8种，‎ ‎∴（和为奇数） 7分 ‎（2）不公平． 8分 ‎∵小明先挑选的概率是（和为奇数），小亮先挑选的概率是（和为偶数），‎ ‎∵，∴不公平． 10分 ‎22．直线与半圆相切． 1分 ‎ 证明：法一：‎ 连接，作于点．‎ O A B E D C 第22题图 F ‎∵，∴． 2分 ‎∵． 3分 ‎∴，‎ ‎∴． 6分 ‎∵，∴． 7分 ‎∴， 8分 ‎∴，‎ ‎∴‎ ‎∴直线与半圆相切． 10分 法二：连接，作于点，作于点．‎ ‎∵，∴．‎ 在中， 3分 ‎∵，，‎ ‎∴四边形是矩形，‎ ‎∴．‎ ‎∵，， 5分 在中，．‎ ‎∵，‎ ‎∴ 8分 ‎∴．‎ ‎∴直线与半圆相切． 10分 六、（每题10分，共20分）‎ ‎23．（1）解：∵，∴．‎ A C D E F B 第23题图 G 又∵，‎ ‎∴， 1分 ‎∵，‎ ‎∴． 2分 ‎（2）过点作于点． 3分 在中，，‎ ‎∴ 4分 又∵，‎ ‎∴．‎ ‎． 6分 在中， 7分 ‎∴， 8分 ‎∴（米） 9分 答：索道长米． 10分 ‎24．解：（1） 2分 ‎． 3分 由 5分 得 6分 ‎∴自变量的取值范围是，且为整数． 7分 ‎（2）∵，∴随的增大而增大，当时，有最小值． 8分 最小值为． 9分 答：一等奖买10件，二等奖买10件，三等奖买30件时，所花的钱数最少，‎ 最少钱数是370元． 10分 七、（本题12分）‎ ‎25．（1）①证明：∵和都是等边三角形，‎ A G C D B F E 图（a）‎ 第25题图 ‎∴． 1分 又∵，，‎ ‎∴，‎ ‎∴． 3分 ‎②法一：由①得，‎ ‎∴．‎ 又∵，‎ ‎∴，‎ ‎∴． 5分 又∵，‎ ‎∴四边形是平行四边形． 6分 法二：证出，‎ 得． 5分 由①得．‎ 得．‎ ‎∴四边形是平行四边形． 6分 ‎（2）①②都成立． 8分 A D C B F E G 图（b）‎ 第25题图 ‎（3）当（或或或或）时，四边形是菱形． 9分 理由：法一：由①得，‎ ‎∴ 10分 又∵，‎ ‎∴． 11分 由②得四边形是平行四边形，‎ ‎∴四边形是菱形． 12分 法二：由①得，‎ ‎∴． 9分 又∵四边形是菱形，‎ ‎∴ 11分 ‎∴． 12分 法三：∵四边形是平行四边形，‎ ‎∴，‎ ‎∴ 9分 ‎∴，‎ ‎∴是等边三角形． 10分 又∵，四边形是菱形，‎ ‎∴，‎ ‎∴ 11分 ‎∴，‎ ‎∵，‎ ‎∴． 12分 八、解答题（本题14分）‎ ‎26．解：（1）法一：由图象可知：抛物线经过原点，‎ 设抛物线解析式为．‎ 把，代入上式得： 1分 解得 3分 ‎∴所求抛物线解析式为 4分 法二：∵，，‎ ‎∴抛物线的对称轴是直线．‎ 设抛物线解析式为（） 1分 把，代入得 ‎ 解得 3分 ‎∴所求抛物线解析式为． 4分 ‎（2）分三种情况：‎ ‎①当，重叠部分的面积是，过点作轴于点，‎ ‎2‎ O A B C x y ‎1‎ ‎1‎ ‎3‎ P 第26题图1‎ Q F ‎∵，在中，，，‎ 在中，，，‎ ‎∴，‎ ‎2‎ O A B C x y ‎1‎ ‎1‎ ‎3‎ 第26题图2‎ Q F G P H ‎∴． 6分 ‎②当，设交于点，作轴于点，‎ ‎，则四边形是等腰梯形，‎ 重叠部分的面积是．‎ ‎∴，‎ ‎∴． 8分 ‎③当，设与交于点，交于点，重叠部分的面积是．‎ ‎2‎ O A B C x y ‎1‎ ‎1‎ ‎3‎ 第26题图3‎ Q F M P N 因为和都是等腰直角三角形，所以重叠部分的面积是．‎ ‎∵，，‎ ‎∴，‎ ‎∴，‎ ‎∴‎ ‎ ． 10分 ‎（3）存在 12分 ‎ 14分