最大面积是多少教案3

最大面积是多少教案3

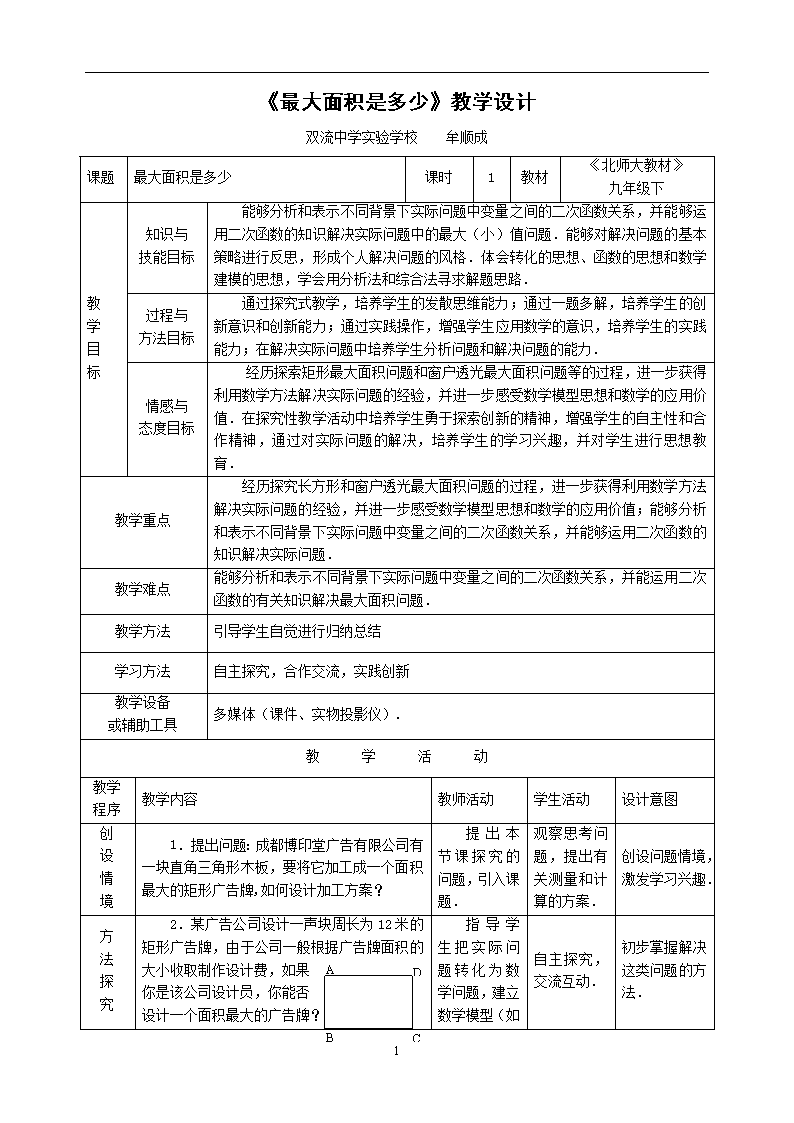
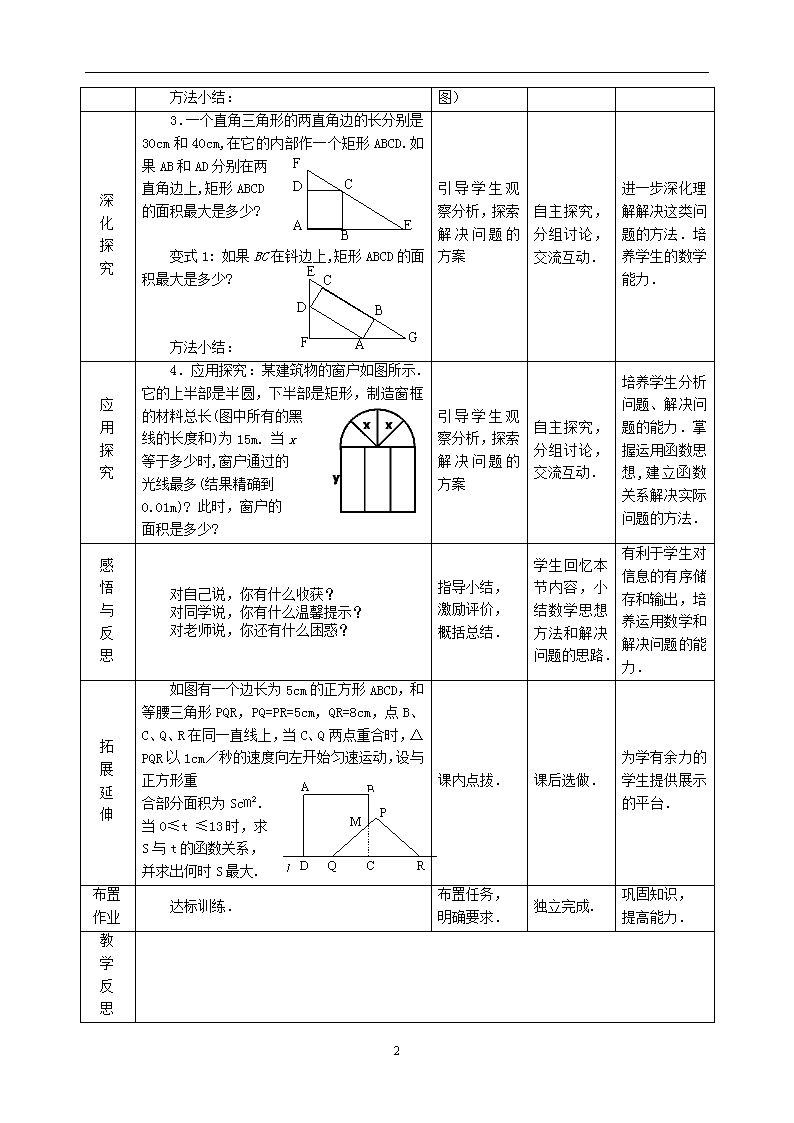
‎《最大面积是多少》教学设计 双流中学实验学校 牟顺成 课题 最大面积是多少 课时 ‎1‎ 教材 ‎《北师大教材》‎ 九年级下 教 学 目 标 知识与 技能目标 能够分析和表示不同背景下实际问题中变量之间的二次函数关系，并能够运用二次函数的知识解决实际问题中的最大（小）值问题．能够对解决问题的基本策略进行反思，形成个人解决问题的风格．体会转化的思想、函数的思想和数学建模的思想，学会用分析法和综合法寻求解题思路．‎ 过程与 方法目标 通过探究式教学，培养学生的发散思维能力；通过一题多解，培养学生的创新意识和创新能力；通过实践操作，增强学生应用数学的意识，培养学生的实践能力；在解决实际问题中培养学生分析问题和解决问题的能力．‎ 情感与 态度目标 经历探索矩形最大面积问题和窗户透光最大面积问题等的过程，进一步获得利用数学方法解决实际问题的经验，并进一步感受数学模型思想和数学的应用价值．在探究性教学活动中培养学生勇于探索创新的精神，增强学生的自主性和合作精神，通过对实际问题的解决，培养学生的学习兴趣，并对学生进行思想教育．‎ 教学重点 经历探究长方形和窗户透光最大面积问题的过程，进一步获得利用数学方法解决实际问题的经验，并进一步感受数学模型思想和数学的应用价值；能够分析和表示不同背景下实际问题中变量之间的二次函数关系，并能够运用二次函数的知识解决实际问题．‎ 教学难点 能够分析和表示不同背景下实际问题中变量之间的二次函数关系，并能运用二次函数的有关知识解决最大面积问题．‎ 教学方法 引导学生自觉进行归纳总结 学习方法 自主探究，合作交流，实践创新 教学设备 或辅助工具 多媒体（课件、实物投影仪）.‎ 教 学 活 动 教学 程序 教学内容 教师活动 学生活动 设计意图 创 设 情 境 ‎1．提出问题：成都博印堂广告有限公司有一块直角三角形木板，要将它加工成一个面积最大的矩形广告牌,如何设计加工方案？‎ 提出本节课探究的问题，引入课题．‎ 观察思考问题，提出有关测量和计算的方案．‎ 创设问题情境，激发学习兴趣．‎ 方 法 探 究 A B C D ‎2．某广告公司设计一声块周长为12米的矩形广告牌，由于公司一般根据广告牌面积的大小收取制作设计费，如果 你是该公司设计员，你能否 设计一个面积最大的广告牌？‎ 自主探究，交流互动．‎ 初步掌握解决这类问题的方法．‎ 3 ‎ 方法小结：‎ 指导学生把实际问题转化为数学问题，建立数学模型（如图）‎ 深 化 探 究 A D B C F E ‎3．一个直角三角形的两直角边的长分别是30cm和40cm,在它的内部作一个矩形ABCD.如果AB和AD分别在两 直角边上,矩形ABCD 的面积最大是多少?‎ E A B C D F G 变式1: 如果BC在钭边上,矩形ABCD的面积最大是多少?‎ 方法小结：‎ 引导学生观察分析，探索解决问题的方案 自主探究，分组讨论，交流互动．‎ 进一步深化理解解决这类问题的方法．培养学生的数学能力．‎ 应 用 探 究 ‎4．应用探究：某建筑物的窗户如图所示.它的上半部是半圆，下半部是矩形，制造窗框的材料总长(图中所有的黑 线的长度和)为15m. 当x 等于多少时,窗户通过的 光线最多(结果精确到 ‎0.01m)? 此时，窗户的 面积是多少?‎ 引导学生观察分析，探索解决问题的方案 自主探究，分组讨论，交流互动．‎ 培养学生分析问题、解决问题的能力．掌握运用函数思想,建立函数关系解决实际问题的方法．‎ 感 悟 与 反 思 ‎ 对自己说，你有什么收获？‎ 对同学说，你有什么温馨提示？‎ 对老师说，你还有什么困惑？‎ 指导小结，‎ 激励评价，‎ 概括总结．‎ 学生回忆本节内容，小结数学思想方法和解决问题的思路．‎ 有利于学生对信息的有序储存和输出，培养运用数学和解决问题的能力．‎ 拓 展 延 伸 M A B C D P Q R l 如图有一个边长为5cm的正方形ABCD，和等腰三角形PQR，PQ=PR=5cm，QR=8cm，点B、C、Q、R在同一直线上，当C、Q两点重合时，△PQR以1cm／秒的速度向左开始匀速运动，设与正方形重 合部分面积为Sc㎡.‎ 当0≤t ≤13时，求 S与t的函数关系，‎ 并求出何时S最大.‎ 课内点拔．‎ 课后选做．‎ 为学有余力的学生提供展示的平台．‎ 布置 作业 达标训练．‎ 布置任务，‎ 明确要求．‎ 独立完成.‎ 巩固知识，‎ 提高能力．‎ 教 学 反 思 3 ‎ 3 ‎