2020九年级数学下册 第2章 直线与圆的位置关系阶段性测试（十三）练习 （新版）浙教版

2020九年级数学下册 第2章 直线与圆的位置关系阶段性测试（十三）练习 （新版）浙教版

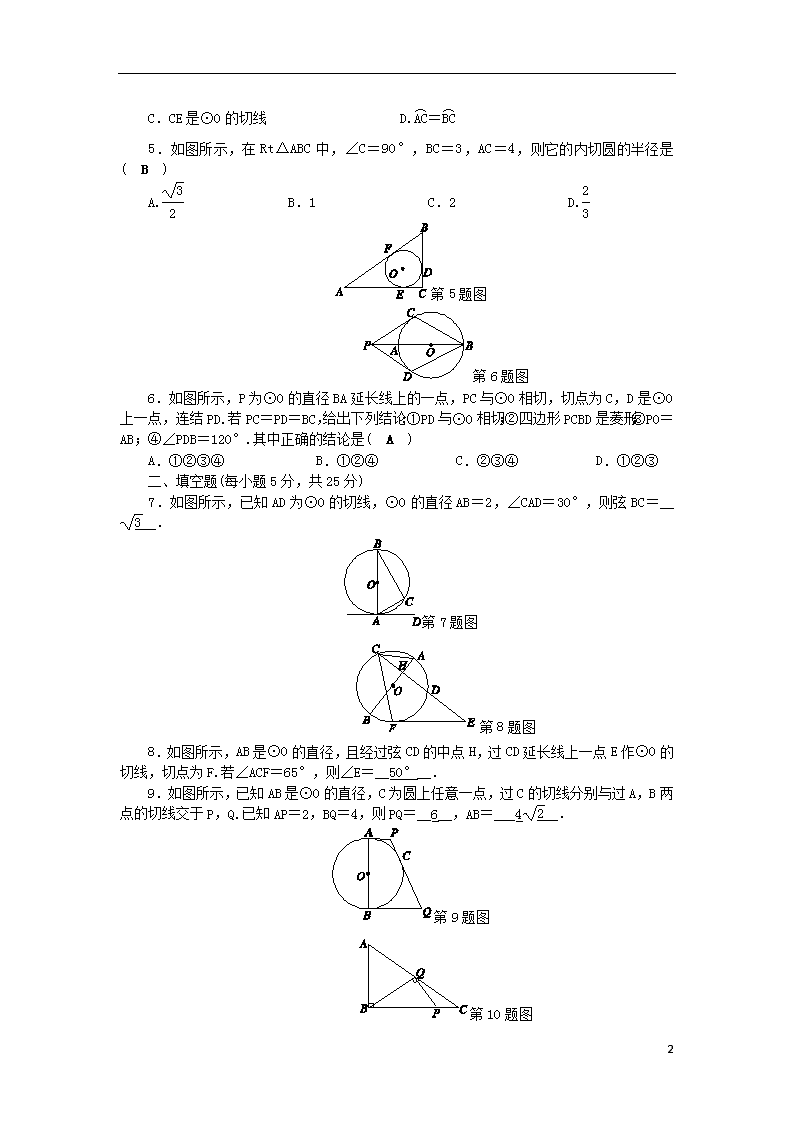
直线与圆的位置关系 阶 段 性 测 试(十三)(见学生单册)‎ ‎[考查范围：直线与圆的位置关系(2.1－2.3)]‎ 一、选择题(每小题5分，共30分)‎ ‎1．下列说法中不正确的是(　C　)‎ A．弦的垂直平分线必过圆心 B．经过切点的直径必垂直于这条切线 C．平分弦的直径必垂直于这条弦 D．等边三角形的外心与内心必重合 ‎2．在△ABC中，∠A＝90°，AB＝‎3 cm，AC＝‎4 cm，若以顶点A为圆心、‎3 cm长为半径作⊙A，则BC与⊙A的位置关系是(　B　)‎ A．相切 B．相交 C．相离 D．无法确定 ‎3．如图所示，在⊙O中，AB为直径，BC为弦，CD切⊙O于点C，连结OC.若∠BCD＝50°，则∠AOC的度数为(　C　)‎ A．40° B．50° C．80° D．100°‎ 第3题图 ‎　　　　　第4题图 ‎4．如图所示，AB是⊙O的弦，半径OC经过AB的中点D，CE∥AB，点F在⊙O上，连结CF，BF.下列所给出的结论中，不正确的是(　B　)‎ A．∠F＝∠AOC B．AB⊥BF 6‎ C．CE是⊙O的切线 D.＝ ‎5．如图所示，在Rt△ABC中，∠C＝90°，BC＝3，AC＝4，则它的内切圆的半径是(　B　)‎ A. B．‎1 ‎ C．2 D. 第5题图 ‎　　　　　第6题图 ‎6．如图所示，P为⊙O的直径BA延长线上的一点，PC与⊙O相切，切点为C，D是⊙O上一点，连结PD.若PC＝PD＝BC，给出下列结论：①PD与⊙O相切；②四边形PCBD是菱形；③PO＝AB；④∠PDB＝120°.其中正确的结论是(　A　)‎ A．①②③④ B．①②④ C．②③④ D．①②③‎ 二、填空题(每小题5分，共25分)‎ ‎7．如图所示，已知AD为⊙O的切线，⊙O的直径AB＝2，∠CAD＝30°，则弦BC＝____．‎ 第7题图 ‎　　　　　第8题图 ‎8．如图所示，AB是⊙O的直径，且经过弦CD的中点H，过CD延长线上一点E作⊙O的切线，切点为F.若∠ACF＝65°，则∠E＝__50°__．‎ ‎9．如图所示，已知AB是⊙O的直径，C为圆上任意一点，过C的切线分别与过A，B两点的切线交于P，Q.已知AP＝2，BQ＝4，则PQ＝__6__，AB＝___4__．‎ 第9题图 ‎　　　　　第10题图 6‎ ‎10．如图所示，在Rt△ABC中，∠ABC＝90°，AB＝3，BC＝4，P是BC边上的动点．设BP＝x，若能在AC边上找到一点Q，使∠BQP＝90°，则x的取值范围是__3≤x≤4__．‎ 第11题图 ‎11．如图所示，直线l：y＝－x＋1与坐标轴交于A，B两点，点M(m，0)是x轴上一动点，以点M为圆心、2个单位长度为半径作⊙M，当⊙M与直线l相切时，则m的值为__2－2或2＋2__．‎ 三、解答题(4个小题，共45分)‎ 第12题图 ‎12．(10分)如图所示，AB为半圆O的直径，C为BA延长线上一点，CD切半圆O于点D.连结OD，作BE⊥CD于点E，交半圆O于点F.已知CE＝12，BE＝9.‎ ‎(1)求证：△COD∽△CBE.‎ ‎(2)求半圆O的半径的长．‎ 解：(1)证明：∵CD切半圆O于点D，‎ ‎∴CD⊥OD，∴∠CDO＝90°，‎ ‎∵BE⊥CD，∴∠E＝90°＝∠CDO，‎ 又∵∠C＝∠C，‎ ‎∴△COD∽△CBE.‎ ‎(2)在Rt△BEC中，CE＝12，BE＝9，‎ ‎∴BC＝＝15，‎ ‎∵△COD∽△CBE.‎ ‎∴＝，即＝，解得r＝.‎ 第13题图 ‎13．(11分)如图1，在△ABC中，CA＝CB，点O在高CH上，OD⊥CA于点D，OE⊥CB于点E，以O为圆心，OD为半径作⊙O.‎ ‎(1)求证：⊙O与CB相切于点E.‎ ‎(2)如图2，若⊙O 过点H，且AC＝5，AB＝6，连结EH，求此时⊙O的半径和△BHE的面积．‎ 解：(1)证明：∵CA＝CB，点O在高CH上，‎ ‎∴CH平分∠ACB，即∠ACH＝∠BCH，‎ ‎∵OD⊥CA，OE⊥CB，∴OE＝OD，‎ ‎∵OE⊥BC，∴⊙O与CB相切于点E.‎ 第13题答图 ‎(2)∵CA＝CB，CH是高，‎ 6‎ ‎∴AH＝BH＝AB＝×6＝3，∴CH＝＝4，‎ ‎∵点O在高CH上，⊙O过点H，‎ ‎∴⊙O与AB相切于点H.‎ ‎∵⊙O与CB相切于点E，‎ ‎∴BE＝BH＝3，∴CE＝2，‎ 连结OE，过H作HF⊥BC于点F，如图2，设半径为R，‎ 在Rt△OCE中，(4－R)2＝R2＋22，解得R＝，‎ ‎∵HF·BC＝CH·BH，∴HF＝＝，‎ ‎∴S△BHE＝×3×＝.‎ 第14题图 ‎14．(12分)如图所示，在△ABC中，AB＝AC，以AB为直径作⊙O交BC于点D，过点D作⊙O 的切线DE交AC于点E，交AB延长线于点F.‎ ‎(1)求证：DE⊥AC.‎ ‎(2)若AB＝10，AE＝8，求BF的长．‎ 第14题答图 解：(1)证明：连结OD、AD，‎ ‎∵DE切⊙O于点D，∴OD⊥DE，‎ ‎∴AB是直径，∴∠ADB＝90°，‎ ‎∵AB＝AC，∴D是BC的中点，‎ 又∵O是AB的中点，∴OD∥AC，‎ ‎∴DE⊥AC.‎ ‎(2)∵AB＝10，∴OB＝OD＝5，由(1)得OD∥AC，∴△ODF∽△AEF，∴＝＝，‎ 设BF＝x，AE＝8，∴＝，解得x＝，经检验x＝是原分式方程的根，且符合题意，∴BF＝.‎ ‎15．(12分)如图所示，△ABC是一块直角三角板，且∠C＝90°，∠A＝30°，现将圆心为点O的圆形纸片放置在三角板内部．‎ 6‎ 第15题图 ‎(1)如图1，当圆形纸片与两直角边AC，BC都相切时，试用直尺与圆规作出射线CO.(不写作法与证明，保留作图痕迹)‎ ‎(2)如图2，将圆形纸片沿着三角板的内部边缘滚动1周，回到起点位置时停止．若BC＝9，圆形纸片的半径为2，求圆心O运动的路径长．‎ 第15题答图 解：(1)如图1所示，射线OC即为所求．‎ ‎(2)如图2，圆心O的运动路径长为C△OO1O2，‎ 过点O1作O1D⊥BC、O1F⊥AC、O1G⊥AB，垂足分别为点D，F，G，‎ 过点O作OE⊥BC，垂足为点E，连结O1B，‎ 过点O2作O2H⊥AB，O2I⊥AC，垂足分别为点H，I，‎ 在Rt△ABC中，∠ACB＝90°，∠A＝30°，‎ ‎∴AC＝＝＝9，AB＝2BC＝18，∠ABC＝60°，‎ ‎∴C△ABC＝9＋9＋18＝27＋9，‎ 第15题答图 ‎∵O1D⊥BC，O1G⊥AB，‎ ‎∴D，G为切点，∴BD＝BG，‎ 在Rt△O1BD和Rt△O1BG中，‎ ‎∵∴△O1BD≌△O1BG(HL)，‎ ‎∴∠O1BG＝∠O1BD＝30°，‎ 在Rt△O1BD中，∠O1DB＝90°，∠O1BD＝30°，‎ 6‎ ‎∴BD＝＝＝2，‎ ‎∴OO1＝9－2－2＝7－2，‎ ‎∵O1D＝OE＝2，O1D⊥BC，OE⊥BC，‎ ‎∴O1D∥OE，‎ ‎∴四边形OEDO1为平行四边形，‎ ‎∵∠OED＝90°，∴四边形OEDO1为矩形，‎ 同理四边形O1O2HG、四边形OO2IF、四边形OECF为矩形，‎ 又OE＝OF，∴四边形OECF为正方形，‎ ‎∵∠O1GH＝∠CDO1＝90°，∠ABC＝60°，‎ ‎∴∠GO1D＝120°，‎ 又∵∠FO1D＝∠O2O1G＝90°，‎ ‎∴∠OO1O2＝360°－90°－90°－120°＝60°＝∠ABC，‎ 同理，∠O1OO2＝90°，‎ ‎∴△OO1O2∽△CBA，‎ ‎∴＝，即＝，‎ ‎∴C△OO1O2＝15＋，即圆心O运动的路径长为15＋.‎ 6‎