2020九年级数学下册 第2章 直线与圆的位置关系 2

2020九年级数学下册 第2章 直线与圆的位置关系 2

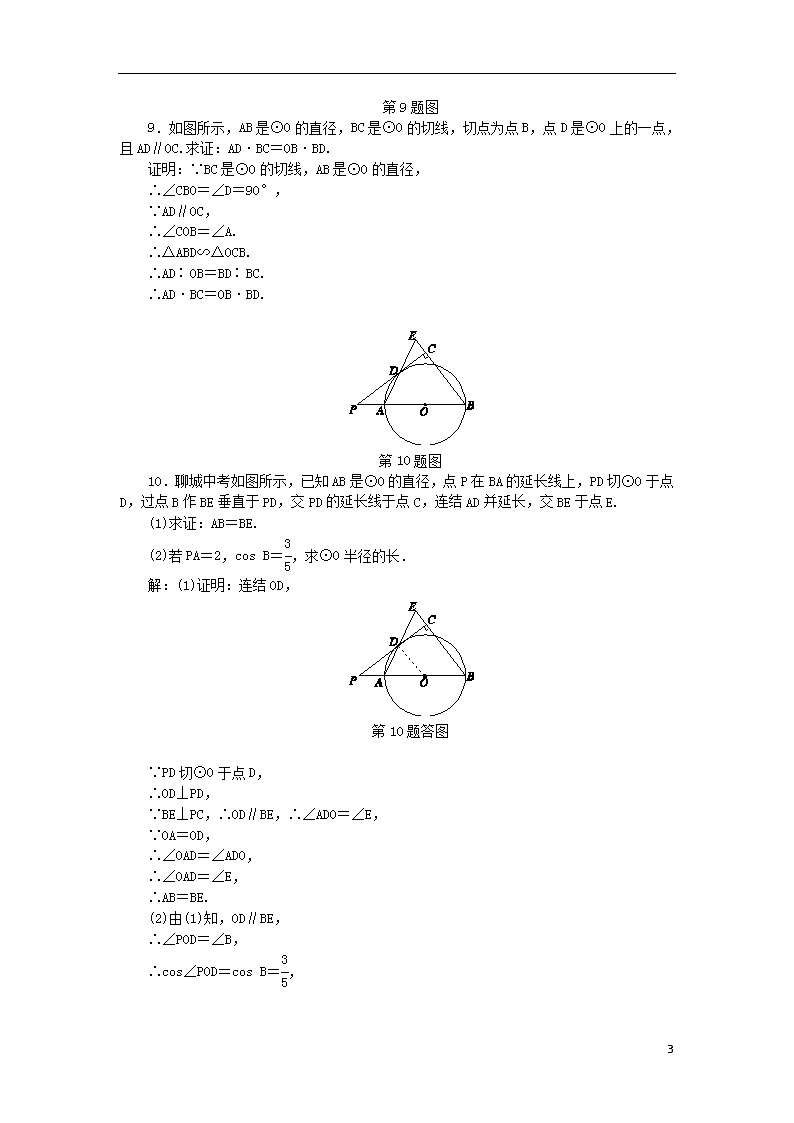
2.1 直线与圆的位置关系(3)‎ ‎(见B本61页)‎ A　练就好基础　基础达标 ‎1．下列说法中正确的是(　A　)‎ A．圆的切线垂直于经过切点的半径 B．垂直于切线的直线必经过切点 C．垂直于切线的直线必经过圆心 D．垂直于半径的直线是圆的切线 第2题图 ‎2．如图所示，PA，PB分别与⊙O相切于A，B两点，若∠C＝65°，则∠P的度数为(　B　)‎ A．45° B．50° C．60° D．70° ‎ ‎3．在平面直角坐标系中，以点(－1，－2)为圆心、与x轴相切的圆的半径长是(　B　)‎ A．1 B．‎2 ‎ C．－1 D．－2‎ ‎4．如图所示是两个同心圆，大圆的弦AB与小圆相切于点C，若AB＝‎6 cm，则图中圆环的面积为(　B　)‎ A．6π cm2 B．9π cm‎2 ‎ C．18π cm2 D．36π cm2‎ 第4题图 6‎ ‎　　　　第5题图 ‎5．2017·日照中考如图所示，AB是⊙O的直径，PA切⊙O于点A，连结PO并延长交⊙O于点C，连结AC，AB＝10，∠P＝30°，则AC的长度是(　A　)‎ A．5　　 B．‎5‎　　 C．5　　 D. ‎6．如图所示，已知∠CAB＝30°，⊙O与AC边相切于点P，且OA＝3，则⊙O的半径为__1.5__．‎ 第6题图 ‎　　　　第7题图 ‎7．如图所示，⊙M与x轴相交于点A(2，0)，B(8，0)，与y轴相切于点C，则圆心M的坐标是　(5，4)　．‎ 第8题图 ‎8．如图所示，已知⊙O的半径等于4，P为⊙O外一点，PA为⊙O的切线，PA＝2，直线PO与⊙O相交于C，D，求：‎ ‎(1)PC的长；‎ ‎(2)sin P的值．‎ 解：(1)连结OA，‎ ‎∵PA是⊙O切线，‎ ‎∴∠PAO＝90°，‎ ‎∴PO＝＝6，‎ ‎∴PC＝PO－OC＝6－4＝2.　‎ ‎(2)在Rt△PAO中，sin P＝＝＝.‎ 6‎ 第9题图 ‎9．如图所示，AB是⊙O的直径，BC是⊙O的切线，切点为点B，点D是⊙O上的一点，且AD∥OC.求证：AD·BC＝OB·BD.‎ 证明：∵BC是⊙O的切线，AB是⊙O的直径，‎ ‎∴∠CBO＝∠D＝90°，‎ ‎∵AD∥OC，‎ ‎∴∠COB＝∠A.‎ ‎∴△ABD∽△OCB.‎ ‎∴AD∶OB＝BD∶BC.‎ ‎∴AD·BC＝OB·BD.‎ 第10题图 ‎10．聊城中考如图所示，已知AB是⊙O的直径，点P在BA的延长线上，PD切⊙O于点D，过点B作BE垂直于PD，交PD的延长线于点C，连结AD并延长，交BE于点E.‎ ‎(1)求证：AB＝BE.‎ ‎(2)若PA＝2，cos B＝，求⊙O半径的长．‎ 解：(1)证明：连结OD，‎ 第10题答图 ‎∵PD切⊙O于点D，‎ ‎∴OD⊥PD，‎ ‎∵BE⊥PC，∴OD∥BE，∴∠ADO＝∠E，‎ ‎∵OA＝OD，‎ ‎∴∠OAD＝∠ADO，‎ ‎∴∠OAD＝∠E，‎ ‎∴AB＝BE.‎ ‎(2)由(1)知，OD∥BE，‎ ‎∴∠POD＝∠B，‎ ‎∴cos∠POD＝cos B＝，‎ 6‎ 在Rt△POD中，cos∠POD＝＝，‎ ‎∵OD＝OA，PO＝PA＋OA＝2＋OA，‎ ‎∴＝，‎ ‎∴OA＝3，‎ ‎∴⊙O半径为3.‎ B　更上一层楼　能力提升 ‎11．如图所示，已知直线CD与⊙O相切于点C，AB为直径，若∠BCD＝40°，则∠ABC的大小等于__50__度．‎ 第11题图 ‎　　　　第12题图 ‎12．2017·衢州中考如图所示，在直角坐标系中，⊙A的圆心A的坐标为(－1，0)，半径为1，点P为直线y＝－x＋3上的动点，过点P作⊙A的切线，切点为Q，则切线长PQ的最小值是__2__．‎ 第13题图 ‎13．2017·北京中考 如图所示，AB是⊙O的一条弦，E是AB的中点，过点E作EC⊥OA于点C，过点B作⊙O的切线交CE的延长线于点D.‎ ‎(1)求证：DB＝DE.‎ ‎(2)若AB＝12，BD＝5，求⊙O的半径．‎ 第13题答图 解：(1)证明：∵AO＝OB，∴∠OAB＝∠OBA，∵BD是切线，‎ 6‎ ‎∴OB⊥BD，‎ ‎∴∠OBD＝90°，∴∠OBE＋∠EBD＝90°，‎ ‎∵EC⊥OA，∴∠CAE＋∠CEA＝90°，‎ ‎∵∠CEA＝∠DEB，∴∠EBD＝∠BED，‎ ‎∴DB＝DE.‎ ‎(2)作DF⊥AB于F，连结OE，∵DB＝DE, ‎ AE＝EB＝6，‎ ‎∴EF＝BE＝3，OE⊥AB，在Rt△DEF中，‎ DE＝BD＝5，EF＝3, ∴DF＝＝4，‎ ‎∴sin∠DEF＝＝， ∵∠AOE＝∠DEF, ‎ ‎∴在Rt△AOE中，sin∠AOE＝＝， ‎ ‎∵AE＝6, ∴AO＝.‎ C　开拓新思路　拓展创新 第14题图 ‎14. 宁波中考如图所示，在矩形ABCD中，AB＝8，AD＝12，过A，D两点的⊙O与BC边相切于点E，则⊙O的半径为____．‎ ‎15．如图所示，⊙O的直径AB＝4，AC是弦，沿AC折叠劣弧，记折叠后的劣弧为.‎ ‎(1)如图(a)，当经过圆心O时，求AC的长．‎ ‎(2)如图(b)，当与AB相切于A时，①画出所在圆的圆心P；②求AC的长．‎ ‎(3)如图(c)，设与直径AB交于点D，DB＝x，试用x的代数式表示AC.‎ ‎　　　 图(a) 　　　　　图(b)　　　　　　图(c)‎ 第15题图 解：(1)作半径OE⊥AC于点F，如图(a)，‎ 6‎ 沿AC折叠劣弧，记折叠后的劣弧为.‎ ‎∴OF＝OE＝×2＝1，∵OE⊥AC，∴AF＝CF.‎ 在Rt△OAF中，OA＝2，OF＝1，∴AF＝＝，‎ ‎∴AC＝2AF＝2.‎ 第15题答图 ‎(2)①过A点作AP⊥AB，再截取AP＝2，则P点为所求，如图(b)；‎ ‎②连结PC，OC，‎ ‎∵AP＝OA＝OC＝PC＝2，‎ ‎∴四边形PAOC为菱形，‎ 而∠PAO＝90°，‎ ‎∴四边形PAOC为正方形，‎ ‎∴AC＝OA＝2.‎ ‎(3)设所在圆的圆心为P，‎ 作PH⊥AB于点H，连结OP，PD，BC，如图(c)，‎ ‎∵AB＝4，BD＝x，∴AD＝4－x，∵PH⊥AD，‎ ‎∴AH＝DH＝AD＝2－x，‎ ‎∴OH＝OA－AH＝x.‎ 在Rt△PAH中，PH＝＝，‎ 在Rt△OPH中，OP＝＝，‎ ‎∵沿AC折叠劣弧，记折叠后的劣弧为，‎ ‎∴OP⊥AC，‎ ‎∵AB为⊙O的直径，∴∠ACB＝90°，∴OP∥BC，‎ ‎∴∠POH＝∠CBA，‎ ‎∴Rt△ACB∽Rt△PHO，∴＝，‎ ‎∴AC＝＝.‎ 6‎