2019年辽宁省大连市中考数学试卷

2019年辽宁省大连市中考数学试卷

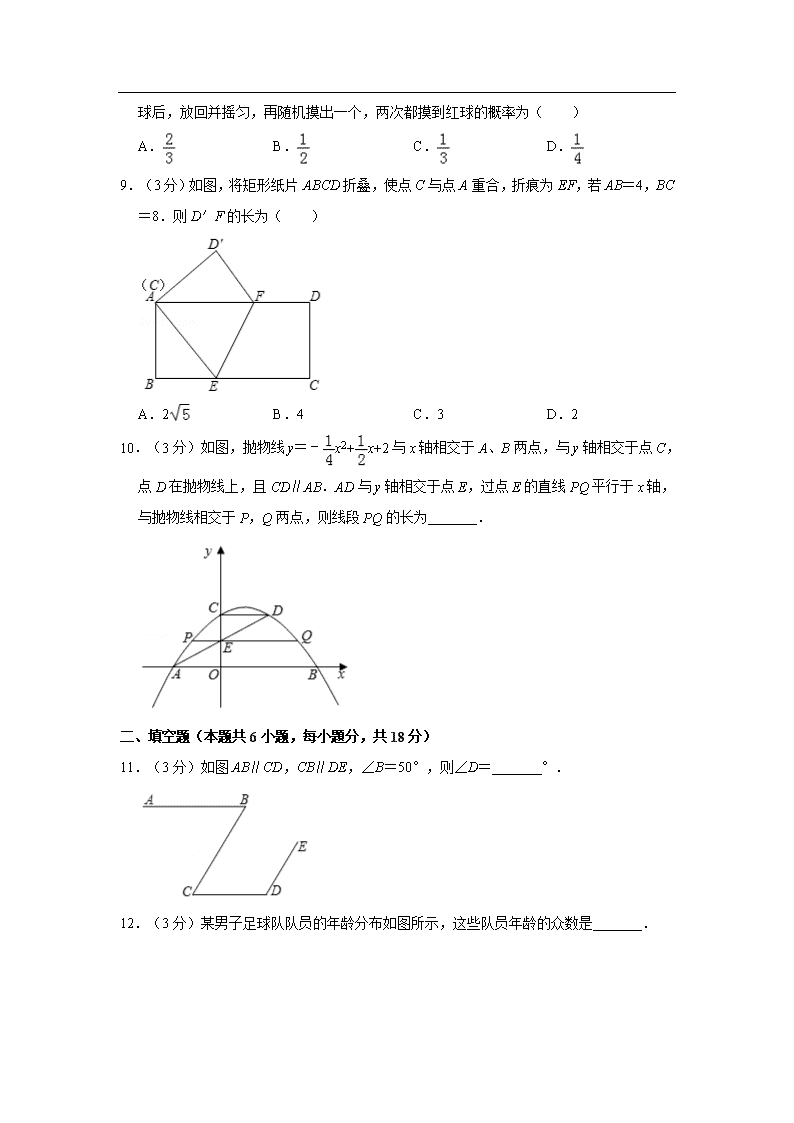
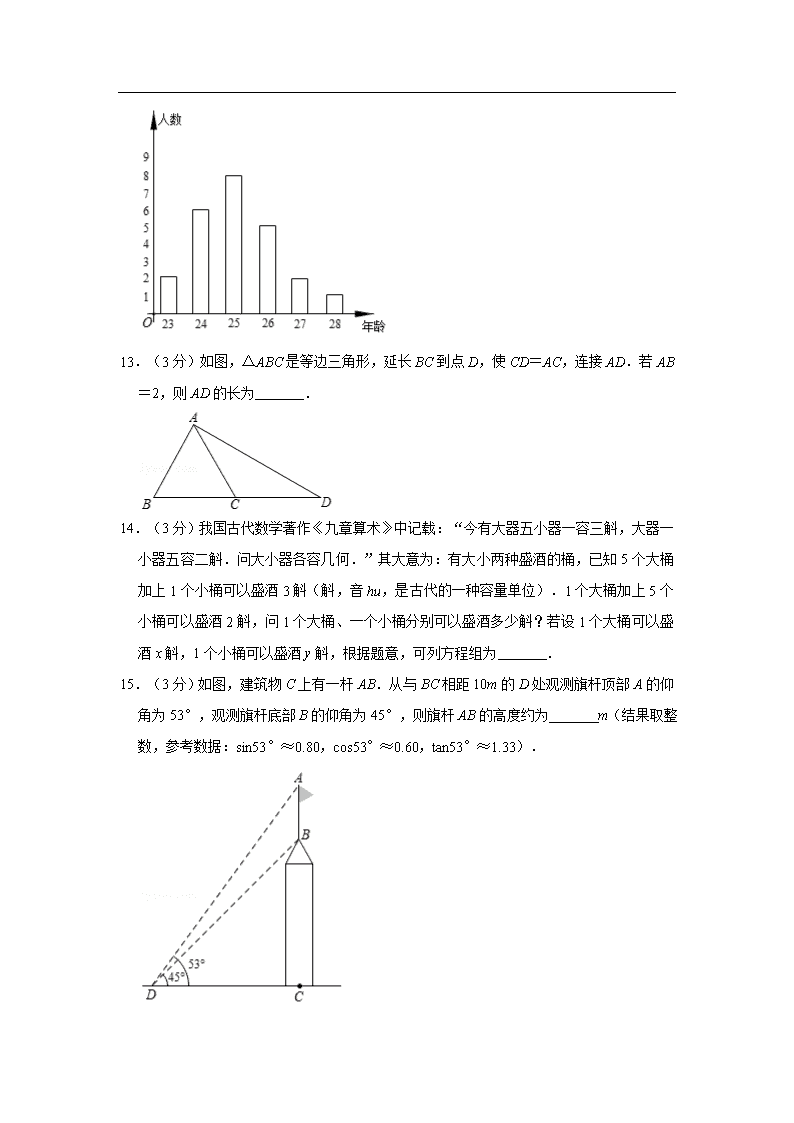
‎2019年辽宁省大连市中考数学试卷 一、选择题（本题共10小題，每小題3分，共30分，在每小题给出的四个选项中，只有一个选项正确）‎ ‎1．（3分）﹣2的绝对值是（　　）‎ A．2 B． C．﹣ D．﹣2‎ ‎2．（3分）如图是一个由4个相同的正方体组成的立体图形，它的主视图是（　　）‎ A． B． ‎ C． D．‎ ‎3．（3分）2019年6月5日，长征十一号运载火箭成功完成了”一箭七星”海上发射技术试验，该火箭重58000kg，将数58000用科学记数法表示为（　　）‎ A．58×103 B．5.8×103 C．0.58×105 D．5.8x104‎ ‎4．（3分）在平面直角坐标系中，将点P（3，1）向下平移2个单位长度，得到的点P′的坐标为（　　）‎ A．（3，﹣1） B．（3，3） C．（1，1） D．（5，1）‎ ‎5．（3分）不等式5x+1≥3x﹣1的解集在数轴上表示正确的是（　　）‎ A． B． ‎ C． D．‎ ‎6．（3分）下列所述图形中，既是轴对称图形又是中心对称图形的是（　　）‎ A．等腰三角形 B．等边三角形 C．菱形 D．平行四边形 ‎7．（3分）计算（﹣2a）3的结果是（　　）‎ A．﹣8a3 B．﹣6a3 C．6a3 D．8a3‎ ‎8．（3分）不透明袋子中装有红、绿小球各一个，除颜色外无其他差别，随机摸出一个小球后，放回并摇匀，再随机摸出一个，两次都摸到红球的概率为（　　）‎ A． B． C． D．‎ ‎9．（3分）如图，将矩形纸片ABCD折叠，使点C与点A重合，折痕为EF，若AB＝4，BC＝8．则D′F的长为（　　）‎ A．2 B．4 C．3 D．2‎ ‎10．（3分）如图，抛物线y＝﹣x2+x+2与x轴相交于A、B两点，与y轴相交于点C，点D在抛物线上，且CD∥AB．AD与y轴相交于点E，过点E的直线PQ平行于x轴，与拋物线相交于P，Q两点，则线段PQ的长为　 　．‎ 二、填空题（本题共6小题，每小題分，共18分）‎ ‎11．（3分）如图AB∥CD，CB∥DE，∠B＝50°，则∠D＝　 　°．‎ ‎12．（3分）某男子足球队队员的年龄分布如图所示，这些队员年龄的众数是　 　．‎ ‎13．（3分）如图，△ABC是等边三角形，延长BC到点D，使CD＝AC，连接AD．若AB＝2，则AD的长为　 　．‎ ‎14．（3分）我国古代数学著作《九章算术》中记载：“今有大器五小器一容三斛，大器一小器五容二斛．问大小器各容几何．”其大意为：有大小两种盛酒的桶，已知5个大桶加上1个小桶可以盛酒3斛（斛，音hu，是古代的一种容量单位）．1个大桶加上5个小桶可以盛酒2斛，问1个大桶、一个小桶分别可以盛酒多少斛？若设1个大桶可以盛酒x斛，1个小桶可以盛酒y斛，根据题意，可列方程组为　 　．‎ ‎15．（3分）如图，建筑物C上有一杆AB．从与BC相距10m的D处观测旗杆顶部A的仰角为53°，观测旗杆底部B的仰角为45°，则旗杆AB的高度约为　 　m（结果取整数，参考数据：sin53°≈0.80，cos53°≈0.60，tan53°≈1.33）．‎ ‎16．（3分）甲、乙两人沿同一条直路走步，如果两人分别从这条多路上的A，B两处同时出发，都以不变的速度相向而行，图1是甲离开A处后行走的路程y（单位：m）与行走时x（单位：min）的函数图象，图2是甲、乙两人之间的距离（单位：m）与甲行走时间x（单位；min）的函数图象，则a﹣b＝　 　．‎ ‎[来源:Z。xx。k.Com]‎ 三、解答题（本题共4小题，17、18、19题各9分，20题12分，共39分）‎ ‎17．（9分）计算：（﹣2）2++6‎ ‎18．（9分）计算：÷+‎ ‎19．（9分）如图，点E，F在BC上，BE＝CF，AB＝DC，∠B＝∠C，求证：AF＝DE．‎ ‎20．（12分）某校为了解八年级男生“立定跳远”成绩的情况，随机选取该年级部分男生进行测试，以下是根据测试成绩绘制的统计图表的一部分．‎ 成绩等级 频数（人）‎ 频率 优秀 ‎15‎ ‎0.3‎ 良好 及格 不及格 ‎5‎ 根据以上信息，解答下列问题 ‎（1）被测试男生中，成绩等级为“优秀”的男生人数为　 　人，成绩等级为“及格”的男生人数占被测试男生总人数的百分比为　 　%；‎ ‎（2）被测试男生的总人数为　 　人，成绩等级为“不及格”的男生人数占被测试男生总人数的百分比为　 　%；‎ ‎（3）若该校八年级共有180名男生，根据调查结果，估计该校八年级男生成绩等级为“良好”的学生人数．‎ 四、解答题（本共3小，其中21、22题各分，23题10分，共28分）‎ ‎21．（9分）某村2016年的人均收入为20000元，2018年的人均收入为24200元 ‎（1）求2016年到2018年该村人均收入的年平均增长率；‎ ‎（2）假设2019年该村人均收入的增长率与前两年的年平均增长率相同，请你预测2019年村该村的人均收入是多少元？‎ ‎22．（9分）如图，在平面直角坐标系xOy中，点A（3，2）在反比例函数y＝（x＞0）的图象上，点B在OA的廷长线上，BC⊥x轴，垂足为C，BC与反比例函数的图象相交于点D，连接AC，AD．‎ ‎（1）求该反比例函数的解析式；‎ ‎（2）若S△ACD＝，设点C的坐标为（a，0），求线段BD的长．‎ ‎23．（10分）如图1，四边形ABCD内接于⊙O，AC是⊙O的直径，过点A的切线与CD的延长线相交于点P．且∠APC＝∠BCP ‎（1）求证：∠BAC＝2∠ACD；‎ ‎（2）过图1中的点D作DE⊥AC，垂足为E（如图2），当BC＝6，AE＝2时，求⊙O的半径．‎ 五、解答题（本题共3小题，其中24题11分，25、26題各12分，共35分）‎ ‎24．（11分）如图，在平面直角坐标系xOy中，直线y＝﹣x+3与x轴，y轴分别相交于点A，B，点C在射线BO上，点D在射线BA上，且BD＝OC，以CO，CD为邻边作▱COED．设点C的坐标为（0，m），▱COED在x轴下方部分的面积为S．求：‎ ‎（1）线段AB的长；‎ ‎（2）S关于m的函数解析式，并直接写出自变量m的取值范围．‎ ‎[来源:Z#xx#k.Com]‎ ‎25．（12分）阅读下面材料，完成（1）﹣（3）题 数学课上，老师出示了这样一道题：如图1，△ABC中，∠BAC＝90°，点D、E在BC上，AD＝AB，AB＝kBD（其中＜k＜1）∠ABC＝∠ACB+∠BAE，∠EAC的平分线与BC相交于点F，BG⊥AF，垂足为G，探究线段BG与AC的数量关系，并证明．同学们经过思考后，交流了自已的想法：‎ 小明：“通过观察和度量，发现∠BAE与∠DAC相等．”‎ 小伟：“通过构造全等三角形，经过进一步推理，可以得到线段BG与AC的数量关系．”‎ ‎……‎ 老师：“保留原题条件，延长图1中的BG，与AC相交于点H（如图2），可以求出的值．”‎ ‎（1）求证：∠BAE＝∠DAC；‎ ‎（2）探究线段BG与AC的数量关系（用含k的代数式表示），并证明；‎ ‎（3）直接写出的值（用含k的代数式表示）．‎ ‎26．（12分）把函数C1：y＝ax2﹣2ax﹣3a（a≠0）的图象绕点P（m，0）旋转180°‎ ‎，得到新函数C2的图象，我们称C2是C1关于点P的相关函数．C2的图象的对称轴与x轴交点坐标为（t，0）．‎ ‎（1）填空：t的值为　 　（用含m的代数式表示）‎ ‎（2）若a＝﹣1，当≤x≤t时，函数C1的最大值为y1，最小值为y2，且y1﹣y2＝1，求C2的解析式；‎ ‎（3）当m＝0时，C2的图象与x轴相交于A，B两点（点A在点B的右侧）．与y轴相交于点D．把线段AD原点O逆时针旋转90°，得到它的对应线段A′D′，若线A′D′与C2的图象有公共点，结合函数图象，求a的取值范围．‎ ‎2019年辽宁省大连市中考数学试卷 参考答案与试题解析 一、选择题（本题共10小題，每小題3分，共30分，在每小题给出的四个选项中，只有一个选项正确）‎ ‎1．（3分）﹣2的绝对值是（　　）‎ A．2 B． C．﹣ D．﹣2‎ ‎【考点】15：绝对值．菁优网版权所有 ‎【分析】根据绝对值是实数轴上的点到原点的距离，可得答案．‎ ‎【解答】解：﹣2的绝对值是2．‎ 故选：A．‎ ‎【点评】本题考查了绝对值，正数的绝对值等于它本身；负数的绝对值等于它的相反数；0的绝对值等于0．‎ ‎2．（3分）如图是一个由4个相同的正方体组成的立体图形，它的主视图是（　　）‎ A． B． ‎ C． D．‎ ‎【考点】U2：简单组合体的三视图．菁优网版权所有 ‎【分析】找到从正面看所得到的图形即可，注意所有的看到的棱都应表现在主视图中．‎ ‎【解答】解：左视图有3列，每列小正方形数目分别为2，1，1．‎ 故选：B．‎ ‎【点评】本题考查了三视图的知识，主视图是从物体的正面看得到的视图．‎ ‎3．（3分）2019年6月5日，长征十一号运载火箭成功完成了”一箭七星”海上发射技术试验，该火箭重58000kg，将数58000用科学记数法表示为（　　）‎ A．58×103 B．5.8×103 C．0.58×105 D．5.8x104‎ ‎【考点】1I：科学记数法—表示较大的数．菁优网版权所有 ‎【分析】科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数．确定n的值时，要看把原数变成a时，小数点移动了多少位，n的绝对值与小数点移动的位数相同．当原数绝对值＞1时，n是正数；当原数的绝对值＜1时，n是负数．‎ ‎【解答】解：将数58000用科学记数法表示为5.8×104．‎ 故选：D．‎ ‎【点评】此题考查科学记数法的表示方法．科学记数法的表示形式为a×10n的形式，其中1≤|a|＜10，n为整数，表示时关键要正确确定a的值以及n的值．‎ ‎4．（3分）在平面直角坐标系中，将点P（3，1）向下平移2个单位长度，得到的点P′的坐标为（　　）‎ A．（3，﹣1） B．（3，3） C．（1，1） D．（5，1）‎ ‎【考点】Q3：坐标与图形变化﹣平移．菁优网版权所有 ‎【分析】根据向下平移，横坐标不变、纵坐标相减列式计算即可得解．‎ ‎【解答】解：将点P（3，1）向下平移2个单位长度，得到的点P′的坐标为（3，1﹣2），即（3，﹣1），‎ 故选：A．‎ ‎【点评】本题考查了坐标与图形变化﹣平移，熟记平移中点的变化规律：横坐标右移加，左移减；纵坐标上移加，下移减是解题的关键．‎ ‎5．（3分）不等式5x+1≥3x﹣1的解集在数轴上表示正确的是（　　）‎ A． B． ‎ C． D．‎ ‎【考点】C4：在数轴上表示不等式的解集；C6：解一元一次不等式．菁优网版权所有 ‎【分析】先求出不等式的解集，再在数轴上表示出来即可．‎ ‎【解答】解：5x+1≥3x﹣1，‎ 移项得5x﹣3x≥﹣1﹣1，‎ 合并同类项得2x≥﹣2，[来源:学,科,网]‎ 系数化为1得，x≥﹣1，‎ 在数轴上表示为：‎ 故选：B．‎ ‎【点评】本题考查了在数轴上表示不等式的解集，把每个不等式的解集在数轴上表示出来（＞，≥向右画；＜，≤向左画），数轴上的点把数轴分成若干段，如果数轴的某一段上面表示解集的线的条数与不等式的个数一样，那么这段就是不等式组的解集．有几个就要几个．在表示解集时“≥”，“≤”要用实心圆点表示；“＜”，“＞”要用空心圆点表示．‎ ‎6．（3分）下列所述图形中，既是轴对称图形又是中心对称图形的是（　　）‎ A．等腰三角形 B．等边三角形 C．菱形 D．平行四边形 ‎【考点】P3：轴对称图形；R5：中心对称图形．菁优网版权所有 ‎【分析】根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解．‎ ‎【解答】解：A、等腰三角形是轴对称图形，不是中心对称图形，故本选项错误；‎ B、等边三角形是轴对称图形，不是中心对称图形，故本选项错误；‎ C、菱形既是轴对称图形，又是中心对称图形，故本选项正确；‎ D、平行四边形不是轴对称图形，是中心对称图形，故本选项错误．‎ 故选：C．‎ ‎【点评】本题考查了中心对称图形与轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．‎ ‎7．（3分）计算（﹣2a）3的结果是（　　）‎ A．﹣8a3 B．﹣6a3 C．6a3 D．8a3‎ ‎【考点】47：幂的乘方与积的乘方．菁优网版权所有 ‎【分析】利用积的乘方的性质求解即可求得答案．‎ ‎【解答】解：（﹣2a）3＝﹣8a3；‎ 故选：A．‎ ‎【点评】此题考查了积的乘方的性质．此题比较简单，注意掌握指数的变化是解此题的关键．‎ ‎8．（3分）不透明袋子中装有红、绿小球各一个，除颜色外无其他差别，随机摸出一个小球后，放回并摇匀，再随机摸出一个，两次都摸到红球的概率为（　　）‎ A． B． C． D．‎ ‎【考点】X6：列表法与树状图法．菁优网版权所有 ‎【分析】用列表法或树状图法可以列举出所有等可能出现的结果，然后看符合条件的占总数的几分之几即可．‎ ‎【解答】解：两次摸球的所有的可能性树状图如下：‎ ‎∴P两次都是红球＝．‎ 故选：D．‎ ‎【点评】考查用树状图或列表法求等可能事件发生的概率，关键是列举出所有等可能出现的结果数，然后用分数表示，同时注意“放回”与“不放回”的区别．‎ ‎9．（3分）如图，将矩形纸片ABCD折叠，使点C与点A重合，折痕为EF，若AB＝4，BC＝8．则D′F的长为（　　）‎ A．2 B．4 C．3 D．2‎ ‎【考点】LB：矩形的性质；PB：翻折变换（折叠问题）．菁优网版权所有 ‎【分析】连接AC交EF于点O，由矩形的性质得出AD＝BC＝8，∠B＝90°，由勾股定理得出AC＝＝4，由折叠的性质得出EF⊥AC，AO＝CO＝AC＝2，证出Rt△FOA∽Rt△ADC，则＝，求出AF＝5，即可得出结果．‎ ‎【解答】解：连接AC交EF于点O，如图所示：‎ ‎∵四边形ABCD是矩形，‎ ‎∴AD＝BC＝8，∠B＝∠D＝90°，‎ AC＝＝＝4，‎ ‎∵折叠矩形使C与A重合时，EF⊥AC，AO＝CO＝AC＝2，‎ ‎∴∠AOF＝∠D＝90°，∠OAF＝∠DAC，‎ ‎∴则Rt△FOA∽Rt△ADC，‎ ‎∴＝，即：＝，‎ 解得：AF＝5，‎ ‎∴D′F＝DF＝AD﹣AF＝8﹣5＝3，‎ 故选：C．‎ ‎【点评】本题考查了折叠的性质、矩形的性质、勾股定理、相似三角形的判定与性质等知识，熟练掌握折叠的性质，证明三角形相似是解题的关键．‎ ‎10．（3分）如图，抛物线y＝﹣x2+x+2与x轴相交于A、B两点，与y轴相交于点C，点D在抛物线上，且CD∥AB．AD与y轴相交于点E，过点E的直线PQ平行于x轴，与拋物线相交于P，Q两点，则线段PQ的长为　2　．‎ ‎【考点】H5：二次函数图象上点的坐标特征；HA：抛物线与x轴的交点．菁优网版权所有 ‎【分析】利用二次函数图象上点的坐标特征可求出点A，B，C，D的坐标，由点A，D的坐标，利用待定系数法可求出直线AD的解析式，利用一次函数图象上点的坐标特征可求出点E的坐标，再利用二次函数图象上点的坐标特征可得出点P，Q 的坐标，进而可求出线段PQ的长．‎ ‎【解答】解：当y＝0时，﹣x2+x+2＝0，‎ 解得：x1＝﹣2，x2＝4，‎ ‎∴点A的坐标为（﹣2，0）；‎ 当x＝0时，y＝﹣x2+x+2＝2，‎ ‎∴点C的坐标为（0，2）；‎ 当y＝2时，﹣x2+x+2＝2，‎ 解得：x1＝0，x2＝2，‎ ‎∴点D的坐标为（2，2）．‎ 设直线AD的解析式为y＝kx+b（k≠0），‎ 将A（﹣2，0），D（2，2）代入y＝kx+b，得：‎ ‎，解得：，‎ ‎∴直线AD的解析式为y＝x+1．‎ 当x＝0时，y＝x+1＝1，‎ ‎∴点E的坐标为（0，1）．‎ 当y＝1时，﹣x2+x+2＝1，‎ 解得：x1＝1﹣，x2＝1+，‎ ‎∴点P的坐标为（1﹣，1），点Q的坐标为（1+，1），‎ ‎∴PQ＝1+﹣（1﹣）＝2．‎ 故答案为：2．‎ ‎【点评】本题考查了抛物线与x轴的交点、二次函数图象上点的坐标特征、待定系数法求一次函数解析式以及一次函数图象上点的坐标特征，利用二次函数图象上点的坐标特征求出点P，Q的坐标是解题的关键．‎ 二、填空题（本题共6小题，每小題分，共18分）‎ ‎11．（3分）如图AB∥CD，CB∥DE，∠B＝50°，则∠D＝　130　°．‎ ‎【考点】JA：平行线的性质．菁优网版权所有 ‎【分析】首先根据平行线的性质可得∠B＝∠C＝50°，再根据BC∥DE可根据两直线平行，同旁内角互补可得答案．‎ ‎【解答】解：∵AB∥CD，‎ ‎∴∠B＝∠C＝50°，‎ ‎∵BC∥DE，‎ ‎∴∠C+∠D＝180°，‎ ‎∴∠D＝180°﹣50°＝130°，‎ 故答案为：130．‎ ‎【点评】此题主要考查了平行线的性质，关键是掌握两直线平行，同旁内角互补． 两直线平行，内错角相等．‎ ‎12．（3分）某男子足球队队员的年龄分布如图所示，这些队员年龄的众数是　25　．‎ ‎【考点】W5：众数．菁优网版权所有 ‎【分析】根据条形统计图找到最高的条形图所表示的年龄数即为众数．‎ ‎【解答】解：观察条形统计图知：为25岁的最多，有8人，‎ 故众数为25岁，‎ 故答案为：25．‎ ‎【点评】考查了众数的定义及条形统计图的知识，解题的关键是能够读懂条形统计图及了解众数的定义，难度较小．‎ ‎13．（3分）如图，△ABC是等边三角形，延长BC到点D，使CD＝AC，连接AD．若AB＝2，则AD的长为　2　．‎ ‎【考点】KK：等边三角形的性质；KO：含30度角的直角三角形．菁优网版权所有 ‎【分析】AB＝AC＝BC＝CD，即可求出∠BAD＝90°，∠D＝30°，解直角三角形即可求得．‎ ‎【解答】解：∵△ABC是等边三角形，‎ ‎∴∠B＝∠BAC＝∠ACB＝60°，‎ ‎∵CD＝AC，‎ ‎∴∠CAD＝∠D，‎ ‎∵∠ACB＝∠CAD+∠D＝60°，‎ ‎∴∠CAD＝∠D＝30°，‎ ‎∴∠BAD＝90°，‎ ‎∴AD＝＝＝2．‎ 故答案为2．‎ ‎【点评】本题考查了等边三角形的性质，等腰三角形的性质以及解直角三角形等，证得△ABD是含30°角的直角三角形是解题的关键．‎ ‎14．（3分）我国古代数学著作《九章算术》中记载：“今有大器五小器一容三斛，大器一小器五容二斛．问大小器各容几何．”‎ 其大意为：有大小两种盛酒的桶，已知5个大桶加上1个小桶可以盛酒3斛（斛，音hu，是古代的一种容量单位）．1个大桶加上5个小桶可以盛酒2斛，问1个大桶、一个小桶分别可以盛酒多少斛？若设1个大桶可以盛酒x斛，1个小桶可以盛酒y斛，根据题意，可列方程组为　　．‎ ‎【考点】1O：数学常识；99：由实际问题抽象出二元一次方程组．菁优网版权所有 ‎【分析】设1个大桶可以盛酒x斛，1个小桶可以盛酒y斛，根据“5个大桶加上1个小桶可以盛酒3斛，1个大桶加上5个小桶可以盛酒2斛”即可得出关于x、y的二元一次方程组．‎ ‎【解答】解：设1个大桶可以盛酒x斛，1个小桶可以盛酒y斛，‎ 根据题意得：，‎ 故答案为．‎ ‎【点评】本题考查了由实际问题抽象出二元一次方程组，根据数量关系列出关于x、y的二元一次方程组是解题的关键．‎ ‎15．（3分）如图，建筑物C上有一杆AB．从与BC相距10m的D处观测旗杆顶部A的仰角为53°，观测旗杆底部B的仰角为45°，则旗杆AB的高度约为　3　m（结果取整数，参考数据：sin53°≈0.80，cos53°≈0.60，tan53°≈1.33）．‎ ‎【考点】TA：解直角三角形的应用﹣仰角俯角问题．菁优网版权所有 ‎【分析】根据正切的定义分别求出AC、BC，结合图形计算即可．‎ ‎【解答】解：在Rt△BCD中，tan∠BDC＝，‎ 则BC＝CD•tan∠BDC＝10，‎ 在Rt△ACD中，tan∠ADC＝，‎ 则AC＝CD•tan∠ADC≈10×1.33＝13.3，‎ ‎∴AB＝AC﹣BC＝3.3≈3（m），‎ 故答案为：3．‎ ‎【点评】本题考查的是解直角三角形的应用﹣仰角俯角问题，掌握仰角俯角的概念、熟记锐角三角函数的定义是解题的关键．‎ ‎16．（3分）甲、乙两人沿同一条直路走步，如果两人分别从这条多路上的A，B两处同时出发，都以不变的速度相向而行，图1是甲离开A处后行走的路程y（单位：m）与行走时x（单位：min）的函数图象，图2是甲、乙两人之间的距离（单位：m）与甲行走时间x（单位；min）的函数图象，则a﹣b＝　　．‎ ‎【考点】FH：一次函数的应用．菁优网版权所有 ‎【分析】从图1，可见甲的速度为＝60，从图2可以看出，当x＝时，二人相遇，即：（60+V已）×＝120，解得：已的速度V已＝80，已的速度快，从图2看出已用了b分钟走完全程，甲用了a分钟走完全程，即可求解．‎ ‎【解答】解：从图1，可见甲的速度为＝60，‎ 从图2可以看出，当x＝时，二人相遇，即：（60+V已）×＝120，解得：已的速度V已＝80，‎ ‎∵已的速度快，从图2看出已用了b分钟走完全程，甲用了a分钟走完全程，‎ a﹣b＝＝，‎ 故答案为．‎ ‎【点评】‎ 本题考查了一次函数的应用，把一次函数和行程问题结合在一起，关键是能正确利用待定系数法求一次函数的解析式，明确三个量的关系：路程＝时间×速度．‎ 三、解答题（本题共4小题，17、18、19题各9分，20题12分，共39分）‎ ‎17．（9分）计算：（﹣2）2++6‎ ‎【考点】79：二次根式的混合运算．菁优网版权所有 ‎【分析】直接利用完全平方公式以及结合二次根式的性质化简进而得出答案．‎ ‎【解答】解：原式＝3+4﹣4+2+6×‎ ‎＝3+4﹣4+2+2‎ ‎＝7．‎ ‎【点评】此题主要考查了二次根式的混合运算，正确化简二次根式是解题关键．‎ ‎18．（9分）计算：÷+[来源:学_科_网]‎ ‎【考点】6C：分式的混合运算．菁优网版权所有 ‎【分析】直接利用分式的乘除运算法则化简，进而利用分式的加减运算法则计算得出答案；‎ ‎【解答】解：原式＝×﹣‎ ‎＝﹣‎ ‎＝．‎ ‎【点评】此题主要考查了分式的混合运算，正确化简是解题关键．‎ ‎19．（9分）如图，点E，F在BC上，BE＝CF，AB＝DC，∠B＝∠C，求证：AF＝DE．‎ ‎【考点】KD：全等三角形的判定与性质．菁优网版权所有 ‎【分析】利用SAS定理证明△ABF≌△DCE，根据全等三角形的性质证明结论．‎ ‎【解答】证明：∵BE＝CF，‎ ‎∴BE+EF＝CF+EF，即BF＝CE，‎ 在△ABF和△DCE中，‎ ‎，‎ ‎∴△ABF≌△DCE（SAS）‎ ‎∴AF＝DE．‎ ‎【点评】本题考查的是全等三角形的判定和性质，掌握全等三角形的判定定理和性质定理是解题的关键．‎ ‎20．（12分）某校为了解八年级男生“立定跳远”成绩的情况，随机选取该年级部分男生进行测试，以下是根据测试成绩绘制的统计图表的一部分．‎ 成绩等级 频数（人）‎ 频率 优秀 ‎15‎ ‎0.3‎ 良好 及格 不及格 ‎5‎ 根据以上信息，解答下列问题 ‎（1）被测试男生中，成绩等级为“优秀”的男生人数为　15　人，成绩等级为“及格”的男生人数占被测试男生总人数的百分比为　90　%；‎ ‎（2）被测试男生的总人数为　50　人，成绩等级为“不及格”的男生人数占被测试男生总人数的百分比为　10　%；‎ ‎（3）若该校八年级共有180名男生，根据调查结果，估计该校八年级男生成绩等级为“良好”的学生人数．‎ ‎【考点】V5：用样本估计总体；V7：频数（率）分布表；VB：扇形统计图．菁优网版权所有 ‎【分析】（1）由统计图表可知，成绩等级为“优秀”‎ 的男生人数为15人，被测试男生总数15÷0.3＝50（人），‎ 成绩等级为“及格”的男生人数占被测试男生总人数的百分比：；‎ ‎（2）被测试男生总数15÷0.3＝50（人），成绩等级为“不及格”的男生人数占被测试男生总人数的百分比：；‎ ‎（3）由（1）（2）可知，优秀30%，及格20%，不及格10%，则良好40%，该校八年级男生成绩等级为“良好”的学生人数180×40%＝72（人）．‎ ‎【解答】解：（1）由统计图表可知，成绩等级为“优秀”的男生人数为15人，‎ 被测试男生总数15÷0.3＝50（人），‎ 成绩等级为“及格”的男生人数占被测试男生总人数的百分比：，‎ 故答案为15，90；‎ ‎（2）被测试男生总数15÷0.3＝50（人），‎ 成绩等级为“不及格”的男生人数占被测试男生总人数的百分比：，‎ 故答案为50，10；‎ ‎（3）由（1）（2）可知，优秀30%，及格20%，不及格10%，则良好40%，‎ 该校八年级男生成绩等级为“良好”的学生人数180×40%＝72（人）‎ 答：该校八年级男生成绩等级为“良好”的学生人数72人．‎ ‎【点评】本题考查的是表格统计图和扇形统计图的综合运用．读懂统计图，从不同的统计图中得到必要的信息是解决问题的关键．表格统计图能清楚地表示出每个项目的数据；扇形统计图直接反映部分占总体的百分比大小．‎ 四、解答题（本共3小，其中21、22题各分，23题10分，共28分）‎ ‎21．（9分）某村2016年的人均收入为20000元，2018年的人均收入为24200元 ‎（1）求2016年到2018年该村人均收入的年平均增长率；‎ ‎（2）假设2019年该村人均收入的增长率与前两年的年平均增长率相同，请你预测2019年村该村的人均收入是多少元？‎ ‎【考点】AD：一元二次方程的应用．菁优网版权所有 ‎【分析】（1）设2016年到2018年该村人均收入的年平均增长率为x，根据某村2016年的人均收入为20000元，2018年的人均收入为24200元，即可得出关于x的一元二次方程，解之取其较小值即可得出结论；‎ ‎（2）由2019年村该村的人均收入＝2018年该村的人均收入×（1+年平均增长率），即可得出结论．‎ ‎【解答】解：（1）设2016年到2018年该村人均收入的年平均增长率为x，‎ 根据题意得：20000（1+x）2＝24200，‎ 解得：x1＝0.1＝10%，x2＝1.1（不合题意，舍去）．‎ 答：2016年到2018年该村人均收入的年平均增长率为10%．‎ ‎（2）24200×（1+10%）＝26620（元）．‎ 答：预测2019年村该村的人均收入是26620元．‎ ‎【点评】本题考查了一元二次方程的应用，解题的关键是：（1）找准等量关系，正确列出一元二次方程；（2）根据数量关系，列式计算．‎ ‎22．（9分）如图，在平面直角坐标系xOy中，点A（3，2）在反比例函数y＝（x＞0）的图象上，点B在OA的廷长线上，BC⊥x轴，垂足为C，BC与反比例函数的图象相交于点D，连接AC，AD．‎ ‎（1）求该反比例函数的解析式；‎ ‎（2）若S△ACD＝，设点C的坐标为（a，0），求线段BD的长．‎ ‎【考点】G5：反比例函数系数k的几何意义；G6：反比例函数图象上点的坐标特征；G7：待定系数法求反比例函数解析式．菁优网版权所有 ‎【分析】（1）把点A（3，2）代入反比例函数y＝，即可求出函数解析式；‎ ‎（2）直线OA的关系式可求，由于点C（a，0），可以表示点B、D的坐标，根据S△ACD＝，建立方程可以解出a的值，进而求出BD的长．‎ ‎【解答】解：（1）∵点A（3，2）在反比例函数y＝（x＞0）的图象上，‎ ‎∴k＝3×2＝6，‎ ‎∴反比例函数y＝；‎ 答：反比例函数的关系式为：y＝；‎ ‎（2）过点A作AE⊥OC，垂足为E，连接AC，‎ 设直线OA的关系式为y＝kx，将A（3，2）代入得，k＝，‎ ‎∴直线OA的关系式为y＝x，‎ ‎∵点C（a，0），把x＝a代入y＝x，得：y＝a，把x＝a代入y＝，得：y＝，‎ ‎∴B（a，），即BC═a，‎ D（a，），即CD＝‎ ‎∵S△ACD＝，‎ ‎∴CD•EC＝，即，解得：a＝6，‎ ‎∴BD＝BC﹣CD＝＝3；‎ 答：线段BD的长为3．‎ ‎【点评】考查正比例函数的图象和性质、反比例函数的图象和性质，将点的坐标转化为线段的长，利用方程求出所设的参数，进而求出结果是解决此类问题常用的方法．‎ ‎23．（10分）如图1，四边形ABCD内接于⊙O，AC是⊙O的直径，过点A的切线与CD的延长线相交于点P．且∠APC＝∠BCP ‎（1）求证：∠BAC＝2∠ACD；‎ ‎（2）过图1中的点D作DE⊥AC，垂足为E（如图2），当BC＝6，AE＝2时，求⊙O的半径．‎ ‎【考点】M5：圆周角定理；M6：圆内接四边形的性质；MC：切线的性质．菁优网版权所有 ‎【分析】（1）作DF⊥BC于F，连接DB，根据切线的性质得到∠PAC＝90°，根据圆周角定理得到∠ADC＝90°，得到∠DBC＝∠DCB，得到DB＝DC，根据线段垂直平分线的性质、圆周角定理证明即可；‎ ‎（2）根据垂径定理求出FC，证明△DEC≌△CFD，根据全等三角形的性质得到DE＝FC＝3，根据射影定理计算即可．‎ ‎【解答】（1）证明：作DF⊥BC于F，连接DB，‎ ‎∵AP是⊙O的切线，‎ ‎∴∠PAC＝90°，即∠P+∠ACP＝90°，‎ ‎∵AC是⊙O的直径，‎ ‎∴∠ADC＝90°，即∠PCA+∠DAC＝90°，‎ ‎∴∠P＝∠DAC＝∠DBC，‎ ‎∵∠APC＝∠BCP，‎ ‎∴∠DBC＝∠DCB，‎ ‎∴DB＝DC，‎ ‎∵DF⊥BC，‎ ‎∴DF是BC的垂直平分线，‎ ‎∴DF经过点O，‎ ‎∵OD＝OC，‎ ‎∴∠ODC＝∠OCD，‎ ‎∵∠BDC＝2∠ODC，‎ ‎∴∠BAC＝∠BDC＝2∠ODC＝2∠OCD；‎ ‎（2）解：∵DF经过点O，DF⊥BC，‎ ‎∴FC＝BC＝3，‎ 在△DEC和△CFD中，‎ ‎，‎ ‎∴△DEC≌△CFD（AAS）‎ ‎∴DE＝FC＝3，‎ ‎∵∠ADC＝90°，DE⊥AC，‎ ‎∴DE2＝AE•EC，‎ 则EC＝＝，‎ ‎∴AC＝2+＝，‎ ‎∴⊙O的半径为．‎ ‎【点评】本题考查的是切线的性质、全等三角形的判定和性质、垂径定理、圆周角定理，掌握圆的切线垂直于经过切点的半径是解题的关键．‎ 五、解答题（本题共3小题，其中24题11分，25、26題各12分，共35分）‎ ‎24．（11分）如图，在平面直角坐标系xOy中，直线y＝﹣x+3与x轴，y轴分别相交于点A，B，点C在射线BO上，点D在射线BA上，且BD＝OC，以CO，CD为邻边作▱COED．设点C的坐标为（0，m），▱COED在x轴下方部分的面积为S．求：‎ ‎（1）线段AB的长；‎ ‎（2）S关于m的函数解析式，并直接写出自变量m的取值范围．[来源:Z,xx,k.Com]‎ ‎【考点】F8：一次函数图象上点的坐标特征；L5：平行四边形的性质．菁优网版权所有 ‎【分析】（1）由直线y＝﹣x+3与令x＝0，或y＝0，分别求出对应的y、x的值，从而确定A、B两点的坐标；‎ ‎（2）分两种情况进行分别探究，①当＜m≤3时，②当0＜m≤时，分别画出相应的图象，根据三角形相似，求出相应的边的长用含有m的代数式表示，再表示面积，从而确定在不同情况下S与m的函数解析式．‎ ‎【解答】解：（1）当x＝0时，y＝3，‎ 当y＝0时，x＝4，‎ ‎∴直线y＝﹣x+3与x轴点交A（4，0），与y轴交点B（0，3）‎ ‎∴OA＝4，OB＝3，‎ ‎∴AB＝，‎ 因此：线段AB的长为5．‎ ‎（2）当CD∥OA时，如图，‎ ‎∵BD＝OC，OC＝m，‎ ‎∴BD＝m，‎ 由△BCD∽△BOA得：‎ ‎，即：，解得：m＝；‎ ‎①当＜m≤3时，如图1所示：过点D作DF⊥OB，垂足为F，‎ 此时在x轴下方的三角形与△CDF全等，‎ ‎∵△BDF∽△BAO，‎ ‎∴，‎ ‎∴DF＝，同理：BF＝m，‎ ‎∴CF＝2m﹣3，‎ ‎∴S△CDF＝＝（2m﹣3）×＝m2﹣2m，‎ 即：S＝m2﹣2m，（＜m≤3）‎ ‎②当0＜m≤时，如图2所示：DE＝m≤，此时点E在△AOB的内部，‎ S＝0 （0＜m≤）；‎ 答：S与m的函数关系式为：S＝m2﹣2m，（＜m≤3）或S＝0 （0＜m≤）．‎ ‎【点评】考查了平行四边形的性质、相似三角形的性质，全等三角形等知识，分类讨论，分别探究在不同情况下，存在的不同函数解析式，根据不同情况，画出相应的图形，再利用所学的知识探究出不同函数解析式．‎ ‎25．（12分）阅读下面材料，完成（1）﹣（3）题 数学课上，老师出示了这样一道题：如图1，△ABC中，∠BAC＝90°，点D、E在BC上，AD＝AB，AB＝kBD（其中＜k＜1）∠ABC＝∠ACB+∠BAE，∠EAC的平分线与BC相交于点F，BG⊥AF，垂足为G，探究线段BG与AC的数量关系，并证明．同学们经过思考后，交流了自已的想法：‎ 小明：“通过观察和度量，发现∠BAE与∠DAC相等．”‎ 小伟：“通过构造全等三角形，经过进一步推理，可以得到线段BG与AC的数量关系．”‎ ‎……‎ 老师：“保留原题条件，延长图1中的BG，与AC相交于点H（如图2），可以求出的值．”‎ ‎（1）求证：∠BAE＝∠DAC；‎ ‎（2）探究线段BG与AC的数量关系（用含k的代数式表示），并证明；‎ ‎（3）直接写出的值（用含k的代数式表示）．‎ ‎【考点】SO：相似形综合题．菁优网版权所有 ‎【分析】（1）利用三角形的外角性质可求解；‎ ‎（2）由直角三角形的性质和角平分线的性质可得AF＝FC，AF＝BF，通过证明△ABG∽△BCA和△ABF∽△BAD，利用相似三角形的性质可求解；‎ ‎（3）通过证明△ABH∽△ACB，可得AB2＝AC×AH，设BD＝m，AB＝km，由勾股定理可求AC的长，可求AH，HC的长，即可求解．‎ ‎【解答】证明：（1）∵AB＝AD ‎∴∠ABD＝∠ADB ‎∵∠ADB＝∠ACB+∠DAC，∠ABD＝∠ABC＝∠ACB+∠BAE ‎∴∠BAE＝∠DAC ‎（2）设∠DAC＝α＝∠BAE，∠C＝β ‎∴∠ABC＝∠ADB＝α+β ‎∵∠ABC+∠C＝α+β+β＝α+2β＝90°，∠BAE+∠EAC＝90°＝α+∠EAC ‎∴∠EAC＝2β ‎∵AF平分∠EAC ‎∴∠FAC＝∠EAF＝β ‎∴∠FAC＝∠C，∠ABE＝∠BAF＝α+β ‎∴AF＝FC，AF＝BF ‎∴AF＝BC＝BF ‎∵∠ABE＝∠BAF，∠BGA＝∠BAC＝90°‎ ‎∴△ABG∽△BCA ‎∴‎ ‎∵∠ABE＝∠BAF，∠ABE＝∠AFB ‎∴△ABF∽△BAD ‎∴，且AB＝kBD，AF＝BC＝BF ‎∴k＝，即 ‎∴‎ ‎（3）∵∠ABE＝∠BAF，∠BAC＝∠AGB＝90°‎ ‎∴∠ABH＝∠C，且∠BAC＝∠BAC ‎∴△ABH∽△ACB ‎∴‎ ‎∴AB2＝AC×AH 设BD＝m，AB＝km，‎ ‎∵‎ ‎∴BC＝2k2m ‎∴AC＝＝km ‎∴AB2＝AC×AH ‎（km）2＝km×AH ‎∴AH＝‎ ‎∴HC＝AC﹣AH＝km﹣＝‎ ‎∴‎ ‎【点评】本题是相似形综合题，考查了相似三角形的判定和性质，直角三角形的性质，灵活运用相似三角形的判定是本题的关键．‎ ‎26．（12分）把函数C1：y＝ax2﹣2ax﹣3a（a≠0）的图象绕点P（m，0）旋转180°‎ ‎，得到新函数C2的图象，我们称C2是C1关于点P的相关函数．C2的图象的对称轴与x轴交点坐标为（t，0）．‎ ‎（1）填空：t的值为　2m﹣1　（用含m的代数式表示）‎ ‎（2）若a＝﹣1，当≤x≤t时，函数C1的最大值为y1，最小值为y2，且y1﹣y2＝1，求C2的解析式；‎ ‎（3）当m＝0时，C2的图象与x轴相交于A，B两点（点A在点B的右侧）．与y轴相交于点D．把线段AD原点O逆时针旋转90°，得到它的对应线段A′D′，若线A′D′与C2的图象有公共点，结合函数图象，求a的取值范围．‎ ‎【考点】HF：二次函数综合题．菁优网版权所有 ‎【分析】（1）C1：y＝ax2﹣2ax﹣3a＝a（x﹣1）2﹣4a，顶点（1，﹣4a）围绕点P（m，0）旋转180°的对称点为（2m﹣1，4a），即可求解；‎ ‎（2）分t＜1、1≤t、t三种情况，分别求解；‎ ‎（3）分a＞0、a＜0两种情况，分别求解．‎ ‎【解答】解：（1）C1：y＝ax2﹣2ax﹣3a＝a（x﹣1）2﹣4a，‎ 顶点（1，﹣4a）围绕点P（m，0）旋转180°的对称点为（2m﹣1，4a），‎ C2：y＝﹣a（x﹣2m+1）2+4a，函数的对称轴为：x＝2m﹣1，‎ t＝2m﹣1，‎ 故答案为：2m﹣1；‎ ‎（2）a＝﹣1时，‎ C1：y＝（x﹣1）2﹣4，‎ ‎①当t＜1时，‎ x＝时，有最小值y2＝，‎ x＝t时，有最大值y1＝﹣（t﹣1）2+4，‎ 则y1﹣y2＝﹣（t﹣1）2+4﹣＝1，无解；‎ ‎②1≤t时，‎ x＝1时，有最大值y1＝4，‎ x＝时，有最小值y2＝﹣（t﹣1）2+4，‎ y1﹣y2＝≠1（舍去）；‎ ‎③当t时，‎ x＝1时，有最大值y1＝4，‎ x＝t时，有最小值y2＝﹣（t﹣1）2+4，‎ y1﹣y2＝（t﹣1）2＝1，‎ 解得：t＝0或2（舍去0），‎ 故C2：y＝（x﹣2）2﹣4＝x2﹣4x；‎ ‎（3）m＝0，‎ C2：y＝﹣a（x+1）2+4a，‎ 点A、B、D、A′、D′的坐标分别为（1，0）、（﹣3，0）、（0，3a）、（0，1）、（﹣3a，0），‎ 当a＞0时，a越大，则OD越大，则点D′越靠左，‎ 当C2过点A′时，y＝﹣a（0+1）2+4a＝1，解得：a＝，‎ 当C2过点D′时，同理可得：a＝1，‎ 故：0＜a或a≥1；‎ 当a＜0时，‎ 当C2过点D′时，﹣3a＝1，解得：a＝﹣，‎ 故：a≤﹣；‎ 综上，故：0＜a或a≥1或a≤﹣．‎ ‎【点评】本题考查的是二次函数综合运用，涉及到一次函数、图形的旋转等，其中（2）（3），要注意分类求解，避免遗漏．‎ 声明：试题解析著作权属菁优网所有，未经书面同意，不得复制发布 日期：2019/7/29 11:42:42；用户：学无止境；邮箱：419793282@qq.com；学号：7910509‎