2020年湖北省随州市中考数学试卷【含答案;word版本试题;可编辑】
2020年湖北省随州市中考数学试卷
一、选择题(本大题共10小题,每小题3分,共30分,每小题给出的四个选项中,有且只有一个是正确的)
1. 2020的倒数是( )
A.-2020 B.2020 C.-12020 D.12020
2. 如图,直线11 // l2,直线1与l1,l2分别交于A,B两点,若∠1=60∘,则∠2的度数是( )
A.60∘ B.100∘ C.120∘ D.140∘
3. 随州7月份连续5天的最高气温分别为:29,30,32,30,34(单位:∘C),则这组数据的众数和中位数分别为( )
A.30,32 B.31,30 C.30,31 D.30,30
4. 一个几何体的三视图如图所示,则该几何体为( )
A.圆柱 B.圆锥 C.四棱柱 D.四棱锥
5. 2x2-4÷1x2-2x的计算结果为( )
A.xx+2 B.2xx+2 C.2xx-2 D.2x(x+2)
6. 我国古代数学著作《孙子算经》中有“鸡兔同笼”问题:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何”.设鸡有x只,兔有y只,则根据题意,下列方程组中正确的是( )
A.x+y=352x+4y=94 B.x+y=354x+2y=94
C.2x+y=35x+4y=94 D.x+4y=352x+y=94
7. 小明从家出发步行至学校,停留一段时间后乘车返回,则下列函数图象最能体现他离家的距离(s)与出发时间(t)之间的对应关系的是( )
A. B.
C. D.
8. 设边长为a的等边三角形的高、内切圆的半径、外接圆的半径分别为h、r、R,则下列结论不正确的是( )
A.h=R+r B.R=2r C.r=34a D.R=33a
9. 将关于x的一元二次方程x2-px+q=0变形为x2=px-q,就可以将x2表示为关于x
12 / 12
的一次多项式,从而达到“降次”的目的,又如x3=x⋅x2=x(px-q)=…,我们将这种方法称为“降次法”,通过这种方法可以化简次数较高的代数式.根据“降次法”,已知:x2-x-1=0,且x>0,则x4-2x3+3x的值为( )
A.1-5 B.3-5 C.1+5 D.3+5
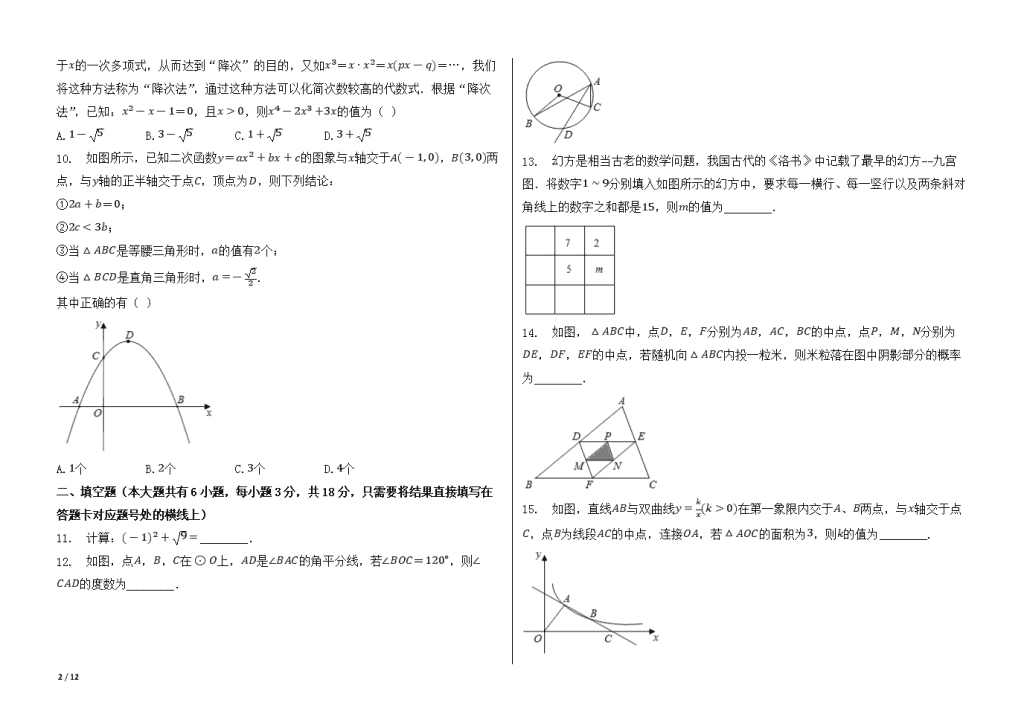
10. 如图所示,已知二次函数y=ax2+bx+c的图象与x轴交于A(-1, 0),B(3, 0)两点,与y轴的正半轴交于点C,顶点为D,则下列结论:
①2a+b=0;
②2c<3b;
③当△ABC是等腰三角形时,a的值有2个;
④当△BCD是直角三角形时,a=-22.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
二、填空题(本大题共有6小题,每小题3分,共18分,只需要将结果直接填写在答题卡对应题号处的横线上)
11. 计算:(-1)2+9=________.
12. 如图,点A,B,C在⊙O上,AD是∠BAC的角平分线,若∠BOC=120∘,则∠CAD的度数为________.
13. 幻方是相当古老的数学问题,我国古代的《洛书》中记载了最早的幻方--九宫图.将数字1∼9分别填入如图所示的幻方中,要求每一横行、每一竖行以及两条斜对角线上的数字之和都是15,则m的值为________.
14. 如图,△ABC中,点D,E,F分别为AB,AC,BC的中点,点P,M,N分别为DE,DF,EF的中点,若随机向△ABC内投一粒米,则米粒落在图中阴影部分的概率为________.
15. 如图,直线AB与双曲线y=kx(k>0)在第一象限内交于A、B两点,与x轴交于点C,点B为线段AC的中点,连接OA,若△AOC的面积为3,则k的值为________.
12 / 12
16. 如图,已知矩形ABCD中,AB=3,BC=4,点M,N分别在边AD,BC上,沿着MN折叠矩形ABCD,使点A,B分别落在E,F处,且点F在线段CD上(不与两端点重合),过点M作MH⊥BC于点H,连接BF,给出下列判断:
①△MHN∽△BCF;
②折痕MN的长度的取值范围为3
0)秒,连接MN,再将线段MN绕点M顺时针旋转90∘,设点N落在点D的位置,若点D恰好落在抛物线上,求t的值及此时点D的坐标;
(3)在(2)的条件下,设P为抛物线上一动点,Q为y轴上一动点,当以点C,P,Q为顶点的三角形与△MDB相似时,请直接写出点P及其对应的点Q的坐标.(每写出一组正确的结果得1分,至多得
12 / 12
参考答案与试题解析
2020年湖北省随州市中考数学试卷
一、选择题(本大题共10小题,每小题3分,共30分,每小题给出的四个选项中,有且只有一个是正确的)
1.D
2.C
3.D
4.A
5.B
6.A
7.B
8.C
9.C
10.B
二、填空题(本大题共有6小题,每小题3分,共18分,只需要将结果直接填写在答题卡对应题号处的横线上)
11.4
12.30∘
13.9
14.116
15.2
16.①②③④
三、解答题(本大题共8小题,共72分,解答应写出必要的演算步骤、文字说明或证明过程)
17.原式=a2+2ab-2ab-2b2
=a2-2b2
当a=5,b=3时,
原式=(5)2-2×(3)2=5-6=-1.
18.∵ △=(2m+1)2-4×1×(m-2)
=4m2+4m+1-4m+8
=4m2+9>0,
∴ 无论m取何值,此方程总有两个不相等的实数根;
由根与系数的关系得出x1+x2=-(2m+1)x1x2=m-2 ,
由x1+x2+3x1x2=1得-(2m+1)+3(m-2)=1,
解得m=8.
19.10
180∘
18
因为年龄在“x<20”的4人中有2名男性,2名女性,
设2名男性用A,B表示,2名女性用C,D表示,
根据题意,画树状图如下:
由上图可知:共有12种等可能的结果,符合条件的结果有2种,
所以恰好抽到2名男性的概率为:212=16.
20.由题意得,在Rt△ABD中,∠ADB=45∘,
∴ AD=AB=25米,
∵ CD=5米,
∴ AC=AD+CD=25+5=30(米),
12 / 12
即A与C之间的距离是30米;
在Rt△ACE中.∠ACE=60∘,AC=30米,
∴ AE=30⋅tan60∘=303(米),
∵ AB=25米,
∴ BE=AE-AB=(303-25)米,
∵ 3≈1.73,
∴ BE≈1.73×30-25=27米.
即天线BE的高度为27米.
21.证明:连接OM,如图1,
∵ OC=OD,
∴ ∠OCM=∠OMC,
在Rt△ABC中,CD是斜边AB上的中线,
∴ CD=12AB=BD,
∴ ∠DCB=∠DBC,
∴ ∠OMC=∠DBC,
∴ OM // BD,
∵ MN⊥BD,
∴ OM⊥MN,
∵ OM过O,
∴ MN是⊙O的切线;
连接DM,CE,
∵ CD是⊙O的直径,
∴ ∠CED=90∘,∠DMC=90∘,
即DM⊥BC,CE⊥AB,
由(1)知:BD=CD=5,
∴ M为BC的中,
∵ sinB=35,
∴ cosB=45,
在Rt△BMD中,BM=BD⋅cosB=4,
∴ BC=2BM=8,
在Rt△CEB中,BE=BC⋅cosB=325,
∴ ED=BE-BD=325-5=75.
22.根据表格数据可知:
前5天的某型号口罩销售价格p(元/只)和销量q(只)与第x天的关系为:
p=x+1,1≤x≤5且x为整数;
q=5x+65,1≤x≤5且x为整数;
当1≤x≤5且x为整数时,
W=(x+1-0.5)(5x+65)
=5x2+1352x+652;
当6≤x≤30且x为整数时,
12 / 12
W=(1-0.5)(-2x2+80x-200)
=-x2+40x-100.
即有W=5x2+1352x+652,1≤x≤5x-x+40x-100,6≤x≤30x ,
当1≤x≤5且x为整数时,售价,销量均随x的增大而增大,
故当x=5时,W有最大值为:495元;
当6≤x≤30且x为整数时,
W=-x2+40x-100=-(x-20)2+300,
故当x=20时,W有最大值为:300元;
由495>300,可知:
第5天时利润最大为495元.
m≥85
23.①如果直角三角形的两条直角边分别为a,b,斜边为c,那么a2+b2=c2.
3
m2,b=c,a+d=m
24.由题意:-b2a=3216a+4b+1=0 ,
解得a=-14b=34 ,
∴ 抛物线的解析式为y=-14x2+34x+1,
令y=0,可得x2-3x-4=0,解得x=-1或4,
∴ A(-1, 0),
令y=0,得到x=1,
∴ C(0, 1),
∴ OA=OC=1,
∴ ∠CAO=45∘.
如图1中,过点C作CE⊥OA于E,过点D作DF⊥AB于F.
∵ ∠NEM=∠DFM=∠NMD=90∘,
∴ ∠NME+∠DMF=90∘,∠DMF+∠MDF=90∘,
∴ ∠NME=∠MDF,
∵ NM=DM,
∴ △MEN≅△DFM(AAS),
∴ NE=MF,EM=DF,
∵ ∠CAO=45∘,AN=2t,AM=3t,
∴ AE=EN=t,
∴ EM=AM-AE=2t,
∴ DF=2t,MF=t,OF=4t-1,
∴ D(4t-1, 2t),
∴ -14(4t-1)2+34(4t-1)+1=2t,
∵ t>0,故可以解得t=34,
经检验,t=34时,M,N均没有达到终点,符合题意,
∴ D(2, 32).
如图3-1中,当点Q在点C的下方,点P在y的右侧,∠QCP=∠MDB时,
12 / 12
取E(12, 0),连接EC,过点E作EG⊥EC交PC于G,
∵ M(54, 0),D(2, 32),B(4, 0)
∴ FM=2-54=34,DM=354,BM=114,BD=52,
∴ DF=2MF,
∵ OC=2OE,
∴ tan∠OCE=tan∠MDF=12,
∴ ∠OCE=∠MDF,
∴ ∠OCP=∠MDB,
∴ ∠ECG=∠FDB,
∴ tan∠ECG=tan∠FDB=43,
∵ EC=52,
∴ EG=253,可得G(116, 23),
∴ 直线CP的解析式为y=-211x+1,
由y=-211x+1y=-14x2+34x+1 ,解得x=0y=0 或x=4111y=39121 ,
∴ P(4111, 39121),
∴ PC=41511,
当MDCQ=BDCP或MDPC=BDCQ时,△QCP与△MDB相似,可得CQ=615242或2050363,
∴ Q(0, -373242)或(0, -1687363).
如图3-2中,当点Q在点C的下方,点P在y的右侧,∠QCP=∠DMB时,设PC交x轴于k.
∵ tan∠OCK=tan∠DMB=2,
∴ OK=2OC=2,
∴ 点K与F重合,
∴ 直线PC的解析式为y=-12x+1,
由y=-12x+1y=-14x2+34x+1 ,解得x=0y=1 或x=5y=-32 ,
∴ P(5, -32),
∴ PC=552,
当DMPC=BMCQ或DMCQ=BMPC时,△QCP与△MDB相似,可得CQ=556或7522,
∴ Q(0, -496)或(0, -5322).
12 / 12
当点Q在点C的下方,点P在y的右侧,∠QCP=∠DBM时,同法可得P(253, -919),Q(0, -25718)或(0, 115199),
当点Q在点C上方,∠QCP=∠DMB时,同法可得P(1, 32),Q(0, 176)或(0, 3722),
当点Q在点C上方,∠QCP=∠MDB时,同法可得P(2511, 171121),Q(0, 617242)或(0, 1613363),
当点Q在点C下方,点P在y轴的左侧时,∠QCP=∠DBM时,同法可得P(-73, -199),Q(0, -5918)或(0, -25199).
12 / 12