2013年山东省滨州市中考数学试题及答案

2013年山东省滨州市中考数学试题及答案

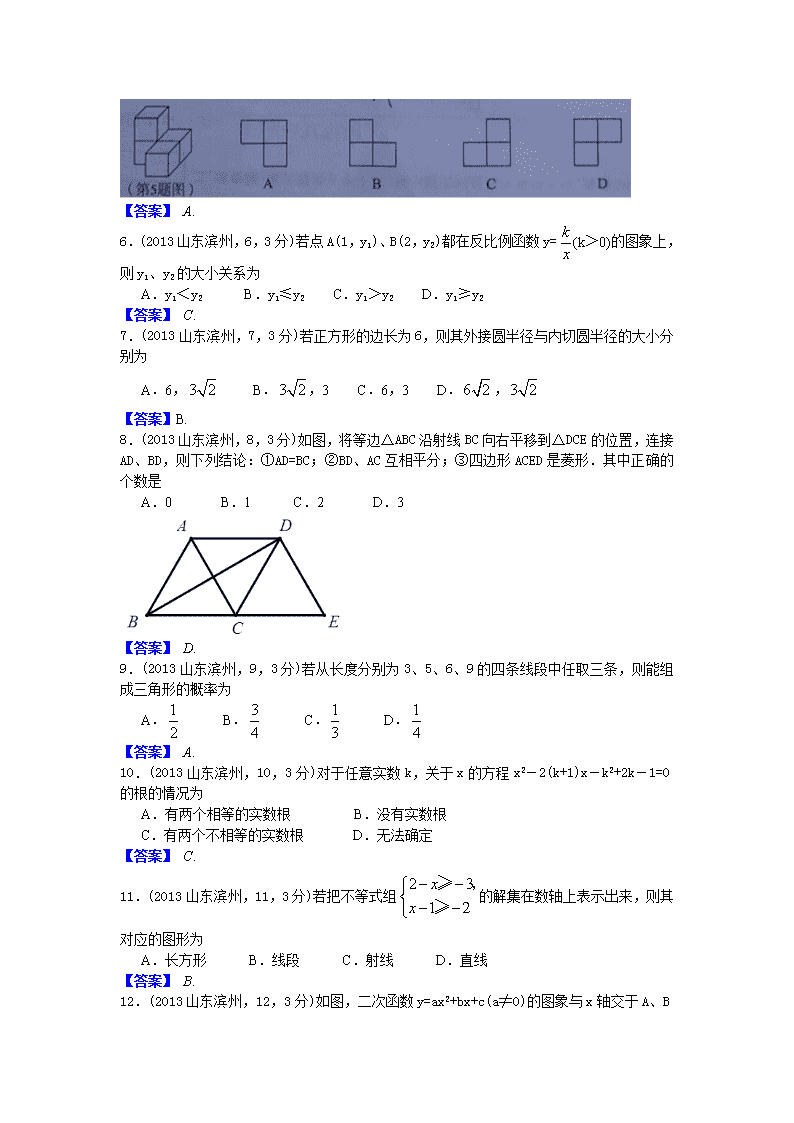
绝密★启用前 试题类型：A 滨州市二〇一三年初中学生学业考试 数学试题 温馨提示： 1.本试卷共 8 页，满分 120 分，考试时间为 120 分钟． 2.请用蓝色或黑色钢笔、圆珠笔直接在试卷上作答(作图可用铅笔)． 3.答卷前请将密封线内的项目填写清楚，并将座号填写在右下角的座号栏内． 一、选择题：本大题共 12 分小题，在每小题的四个选项中只有一个是正确的，请把正确的 选项选出来，并将其字母标号填写在答题栏内．每小题选对得 3 分，错选、不选或多选均记 0 分，满分 36 分． 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 1．(2013 山东滨州，1，3 分)计算 1 3 － 1 2 ，正确的结果为 A． 1 5 B．－ 1 5 C． 1 6 D．－ 1 6 【答案】 D. 2．(2013 山东滨州，2，3 分)化简 3a a ，正确的结果为 A．a B．a2 C．a－1 D．a－2 【答案】 B. 3．(2013 山东滨州，3，3 分)把方程 1 2 x=1 变形为 x=2，其依据是 A．等式的性质 1 B．等式的性质 2 C．分式的基本性质 D．不等式的性质 1 【答案】 B. 4．(2013 山东滨州，4，3 分)如图，在⊙O 中圆心角∠BOC=78°，则圆周角∠BAC 的大小为 A．156° B．78° C．39° D．12° 【答案】 C. 5．(2013 山东滨州，5，3 分)左图所示的几何体是由若干个大小相同的小正方体组成的．若 从正上方看这个几何体，则所看到的平面图形是 【答案】 A. 6．(2013 山东滨州，6，3 分)若点 A(1，y1)、B(2，y2)都在反比例函数 y= k x (k＞0)的图象上， 则 y1、y2 的大小关系为 A．y1＜y2 B．y1≤y2 C．y1＞y2 D．y1≥y2 【答案】 C. 7．(2013 山东滨州，7，3 分)若正方形的边长为 6，则其外接圆半径与内切圆半径的大小分 别为 A．6，3 2 B．3 2 ，3 C．6，3 D． 6 2 ，3 2 【答案】B. 8．(2013 山东滨州，8，3 分)如图，将等边△ABC 沿射线 BC 向右平移到△DCE 的位置，连接 AD、BD，则下列结论：①AD=BC；②BD、AC 互相平分；③四边形 ACED 是菱形．其中正确的 个数是 A．0 B．1 C．2 D．3 【答案】 D. 9．(2013 山东滨州，9，3 分)若从长度分别为 3、5、6、9 的四条线段中任取三条，则能组 成三角形的概率为 A． 1 2 B． 3 4 C． 1 3 D． 1 4 【答案】 A. 10．(2013 山东滨州，10，3 分)对于任意实数 k，关于 x 的方程 x2－2(k+1)x－k2+2k－1=0 的根的情况为 A．有两个相等的实数根 B．没有实数根 C．有两个不相等的实数根 D．无法确定 【答案】 C. 11．(2013 山东滨州，11，3 分)若把不等式组 2 x x        ≥ ， ≥ 的解集在数轴上表示出来，则其 对应的图形为 A．长方形 B．线段 C．射线 D．直线 【答案】 B. 12．(2013 山东滨州，12，3 分)如图，二次函数 y=ax2+bx+c(a≠0)的图象与 x 轴交于 A、B 两点，与 y 轴交于 C 点，且对称轴为 x=1，点 B 坐标为(－1，0)．则下面的四个结论：①2a+b=0； ②4a－2b+c＜0；③ac＞0；④当 y＜0 时，x＜－1 或 x＞2．其中正确的个数是 A．1 B．2 C．3 D．4 【答案】 B. 二、填空题：本大题共 6 各小题，每小题填对最后结果得 4 分，满分 24 分． 13．(2013 山东滨州，13，4 分)分解因式：5x2－20=______________． 【答案】 5(x+2)(x－2). 14．(2013 山东滨州，14，4 分)在△ABC 中，∠C=90°，AB=7，BC=5，则边 AC 的长为 ______________． 【答案】 2 6 15．(2013 山东滨州，15，4 分)在等腰△ABC 中，AB=AC，∠A=50°，则∠B=______________． 【答案】 65° 16．(2013 山东滨州，16，4 分)一元二次方程 2x2－3x+1=0 的解为______________． 【答案】x1=1，x2= 1 2 . 17．(2013 山东滨州，17，4 分)在 ABCD 中，点 O 是对角线 AC、BD 的交点，点 E 是边 CD 的中点，且 AB=6，BC=10，则 OE=______________． 【答案】 A. 18．(2013 山东滨州，18，4 分)观察下列各式的计算过程： 5×5=0×1×100+25， 15×15=1×2×100+25， 25×25=2×3×100+25， 35×35=3×4×100+25， …… …… 请猜测，第 n 个算式(n 为正整数)应表示为____________________________． 【答案】 [10(n－1)+5]×[10(n－1)+5]=100n(n－1)+25. 三、解答题：本大题共 7 个小题，满分 60 分．解答时请写出必要的演推过程． 19．(2013 山东滨州，19，6 分)(本小题满分 6 分，请在下列两个小题中，任选其一完成即 可) (1)解方程组： 3 4 19x y x y       ， (2)解方程： 3 5 2 .2 3 x x  【解答过程】 解：(1) 3 4 19x y x y       ，① ② . 由②，得 x=4+y，③ 把③代入①，得 3(4+y)+4y=19， 12+3y+4y=19， y=1． 把 y=1 代入③，得 x=4+1=5． ∴方程组的解为 5x y    ， (2)去分母，得 3(3x+5)=2(2x－1)． 去括号，得 9x+15=4x－2． 移项、合并同类项，得 5x=－17． 系数化为 1，得 x=－17 5 ． 20．(2013 山东滨州，20，7 分)(计算时不能使用计算器) 计算： 3 3 －( 3 )2+ 0( 3)  － 27 + 3 2 ． 【解答过程】 解：原式= 3 －3+1－3 3 +2－ 3 =－3 3 ． 21．(2013 山东滨州，21，8 分)某高中学校为使高一新生入校后及时穿上合身的校服，现提 前对某校九年级三班学生即将所穿校服型号情况进行了摸底调查，并根据调查结果绘制了如 下两个不完整的统计图(校服型号以身高作为标准，共分为 6 种型号)． 根据以上信息，解答下列问题： (1)该班共有多少名学生？其中穿 175 型校服的学生有多少？ (2)在条形统计图中，请把空缺的部分补充完整； (3)在扇形统计图中，请计算 185 型校服所对应扇形圆心角的大小； (4)求该班学生所穿校服型号的众数和中位数． 【解答过程】 解：(1)15÷30%=50(人)，50×20%=10(人)， 即该班共有 50 名学生，其中穿 175 型校服的学生有 10 人． (2)补充如下： (3)185 型的人数是 50－3－15－15－10－5=2(人)，圆心角的度数为 360°× 2 50 =14.4°． (4)165 型和 170 型出现的次数最多都是 15 次，故众数是 165 和 170；共 50 个数据，第 25 和第 26 个数据都是 170，故中位数是 170． 22．(2013 山东滨州，22，8 分) 如图，在△ABC 中，AB=AC，点 O 在边 AB 上，⊙O 过点 B 且分别与边 AB、BC 相交于 点 D、E，EF⊥AC，垂足为 F．求证：直线 EF 是⊙O 的切线． 【解答过程】 证明：连接 OE， ∵OB=OE， ∴∠B=∠OEB． ∵AB=AC， ∴∠B=∠C． ∴∠OEB=∠C． ∴OE∥AC． ∵EF⊥AC， ∴OE⊥EF． ∴直线 EF 是⊙O 的切线． 23．(2013 山东滨州，23，9 分) 某高中学校为高一新生设计的学生单人桌的抽屉部分是长方体形，抽屉底面周长为 180cm， 高为 20cm．请通过计算说明，当底面的宽 x 为何值时，抽屉的体积 y 最大？最大为多少？(材 质及其厚度等暂忽略不计) 【解答过程】 解：根据题意，得 y=20x(180 2 －x)， 整理，得 y=－20x2+1800x． ∵y=－20x2+1800x=－20(x2－90x+2025)+40500=－20(x－45)2+40500， ∵－20＜0，∴当 x=45 时，函数有最大值，y 最大值=40500， 即当底面的宽为 45cm 时，抽屉的体积最大，最大为 40500cm2． 24．(2013 山东滨州，24，10 分) 某高中学校为高一新生设计的学生板凳的正面视图如图所示．其中 BA=CD，BC=20cm，BC、 EF 平行于地面 AD 且到地面 AD 的距离分别为 40cm、8cm，为使板凳两腿底端 A、D 之间 的距离为 50cm，那么横梁 EF 应为多长？(材质及其厚度等暂忽略不计) 【解答过程】 解：过点 C 作 CM∥AB，交 EF、AD 于 N、M，作 CP⊥AD，交 EF、AD 于 Q、P． 由题意，得四边形 ABCM 是平行四边形， ∴EN=AM=BC=20(cm)． ∴MD=AD－AM=50－20=30(cm)． 由题意知 CP=40cm，PQ=8cm， ∴CQ=32cm． ∵EF∥AD， ∴△CNF∽△CMD． ∴ NF MD = CQ CP ， 即 30 NF = 32 40 ． 解得 NF=24(cm)． ∴EF=EN+NF=20+24=44(cm)． 答：横梁 EF 应为 44cm． 25．(2013 山东滨州，25，12 分) 根据要求，解答下列问题： (1)已知直线 l1 的函数解析式为 y=x，请直接写出过原点且与 l1 垂直的直线 l2 的函数表达 式； (2)如图，过原点的直线 l3 向上的方向与 x 轴的正方向所成的角为 30°． ①求直线 l3 的函数表达式； ②把直线 l3 绕原点 O 按逆时针方向旋转 90°得到直线 l4，求直线 l4 的函数表达式． (3)分别观察(1)、(2)中的两个函数表达式，请猜想：当两直线互相垂直时，它们的函数 表达式中自变量的系数之间有何关系？请根据猜想结论直接写出过原点且与直线 y=－ 1 5 x 垂直的直线 l5 的函数表达式． 【解答过程】 解：(1)y=－x． (2)①如图，在直线 l3 上任取一点 M，作 MN⊥x 轴，垂足为 N． 设 MN 的长为 1，∵∠MON=30°，∴ON= 3 ． 设直线 l3 的表达式为 y=kx，把( 3 ，1)代入 y=kx，得 1= 3 k，k= 3 3 ． ∴直线 l3 的表达式为 y= 3 3 x． ②如图，作出直线 l4，且在 l4 取一点 P，使 OP=OM，作 PQ⊥y 轴于 Q， 同理可得∠POQ=30°，PQ=1，OQ= 3 ， 设直线 l4 的表达式为 y=kx，把(－1， 3 )代入 y=kx，得 3 =－k，∴k=－ 3 ． ∴直线 l4 的表达式为 y==－ 3 x． (3)当两直线互相垂直时，它们的函数表达式中自变量的系数互为负倒数，即两系数的乘积 等于－1． ∴过原点且与直线 y=－ 1 5 x 垂直的直线 l5 的函数表达式为 y=5x．