16 中 2016 学年第二学期期中检测初一数学试题

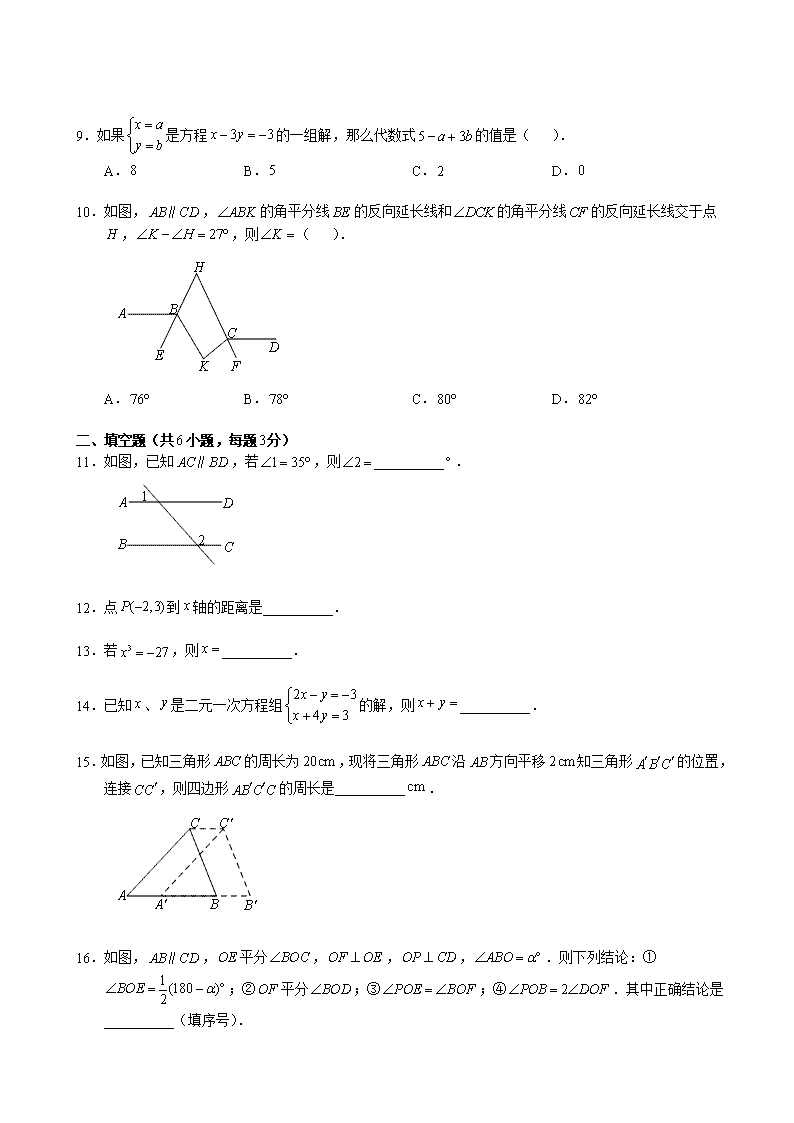
16 中 2016 学年第二学期期中检测初一数学试题

16 中 2016 学年第二学期期中检测初一数学试题 一、选择题（共 10 小题，每题 3 分） 1．下列图形中，不能通过其中一个四边形平移得到的是（ ）． A． B． C． D． 2．下列命题中真命题的是（ ）． A．同位角相等 B．两点之间，线段最短 C．相等的角是对顶角 D．互补的角是邻补角 3．实数 2( 3) 的平方根是（ ）． A． 3 B． 3 C． 3 D． 3 4．下列实数： 3 ， 4 ， π 3 ，10 7 ， 3 8 ，1.010010001， 3.14 ，其中无理数有（ ）． A．1个 B． 2 个 C．3个 D． 4 个 5．点 1 ,12     在（ ）． A．第一象限 B．第二象限 C．第三象限 D．第四象限 6．小华将平面直角坐标系中的 ( 4,3)A  沿着 x 轴方向向左平移了 3个单位得到了 B 点，则 B 点的坐标是 （ ）． A． ( 7,3) B． ( 1,3) C． ( 4,0) D． ( 4,6) 7．如图， AB CD‖ ， DA AC ，垂足为 A ，若 35ADC   ，则 1 的度数是（ ）． A． 65 B．55 C． 45 D． 35 8．小龙和小刚两人玩“打弹珠”游戏，小龙对小刚说：“你把珠子的一半给我 ，我就有10 颗珠子”，小刚却 说：“只要把你的 1 3 给我，我就有10 颗．”如果设小刚的弹珠数为 x 颗，小龙的弹珠数为 y 颗，则列出的 方程组是（ ）． A． 2 20 3 30 x y x y      B． 2 10 3 10 x y x y      C． 2 20 3 10 x y x y      D． 2 10 3 30 x y x y      9．如果 x a y b    是方程 3 3x y   的一组解，那么代数式 5 3a b  的值是（ ）． A．8 B．5 C． 2 D． 0 10．如图，AB CD‖ ， ABK 的角平分线 BE 的反向延长线和 DCK 的角平分线CF 的反向延长线交于点 H ， 27K H     ，则 K  （ ）． A． 76 B． 78 C．80 D．82 二、填空题（共 6 小题，每题 3分） 11．如图，已知 AC BD‖ ，若 1 35   ，则 2  __________ ． 12．点 ( 2,3)P  到 x 轴的距离是__________． 13．若 3 27x   ，则 x  __________． 14．已知 x 、 y 是二元一次方程组 2 3 4 3 x y x y       的解，则 x y  __________． 15．如图，已知三角形 ABC 的周长为 20cm ，现将三角形 ABC 沿 AB 方向平移 2cm 知三角形 A B C   的位置， 连接 CC，则四边形 AB C C  的周长是__________ cm ． 16．如图，AB CD‖ ，OE 平分 BOC ，OF OE ，OP CD ， ABO    ．则下列结论：① 1 (180 )2BOE     ； ② OF 平分 BOD ；③ POE BOF   ；④ 2POB DOF   ．其中正确结论是__________（填序号）． 三、解答题（共 72 分） 17．（8分）化简求值 （1） 319 6 84    （ 2 ） 2 5 3 5   18．（10 分）解二元一次方程组 （1） 2 3 7 3 8 x y x y      （ 2 ） 2 5 4 1 x y x y       19．（10 分）如图，在平面直角坐标系中有三个点 ( 3,2)A  ， ( 5,1)B  ， ( 2,0)C  ， ( , )P a b 是三角形的边 AC 上 一点，三角形 ABC 经平移后得到三角形 A B C   ，点 P 的对应点为 ( 4, 3)P a b   ． （1）画出平移后的三角形 A B C   ，写出点 A 、 B 、 C三个点的坐标． （ 2 ）求四边形 ACC A  的面积． 20．（8分）如图，已知 AC AB ， ED AB ，垂足分别为 A 、 D ， 65CAF   ． 求 DGE 的度数． 21．（12 分）如图， AP 、 CP 分别平分 BAC 、 ACD ， 90P   ，设 BAP x   ． （1）用 x 表示 ACP ． （ 2 ）求证： AB CD‖ ． （ 3）若 AP CF‖ ，求证： FC 平分 DCE ． 22．（12 分）一家商店进行装修，若请甲、乙两个装修组同时施工，8天可以完成，需付两组费用共3520 元， 若先请甲组单独做 6 天，再请乙组单独做12 天可以完成，需付费用 3480 元，问： （1）甲、乙两组工作一天，商店各应付多少钱？ （ 2 ）已知甲单独完成需12 天，乙单独完成需 24 天，单独请哪个组，商店所需费用最少？ （ 3）若装修完后，商店每天可赢利 200 元，根据前面的结论，你认为如何安排施工更有利于商店？请 你帮助商店决策． 23．（12 分）如图，以直角三角形 AOC 的直角顶点 O 为原点，以 OC 、OA所在直线为 x 轴和 y 轴建立平面 直角坐标系，点 (0, )A a ， ( ,0)C b 满足 2 2 0a b b    ． D 为线段 AC 的中点． （1）则 A 点的坐标为__________；点 C 的坐标为__________． （ 2 ）在平面直角坐标系中，以任意两点 1 1( , )P x y 、 2 2( , )Q x y 为端点的线段中点坐标为 1 2 1 2,2 2 x x y y      ．则 D 点的坐标为__________． （ 3）已知坐标轴上有两动点 P 、Q 同时出发， P 点从 C 点出发沿 x 轴负方向以1个单位长度每秒的速 度匀速移动， Q 点从 O 点出发以 2 个单位长度每秒的速度沿 y 轴正方向移动，点 Q 到达 A 点整 个运动随之结束．设运动时间为 ( 0)t t  秒．问：是否存在这样的 t ，使 ODP ODQS S△ △ ，若存在， 请求出 t 的值；若不存在，请说明理由． （ 4 ）点 F 是线段 AC 上一点，满足 FOC FCO   ，点 G 是第二象限中一点，连 OG ，使得 AOG AOF   ．点 E 是线段 OA上一动点，连 CE 交 OF 于点 H ，当点 E 在线段OA 上运动的 过程中， OHC ACE OEC     的值是否会发生变化？若不变，请求出它的值；若变化，请说明理由．