2020年九年级数学上册圆中三大基本定理

2020年九年级数学上册圆中三大基本定理

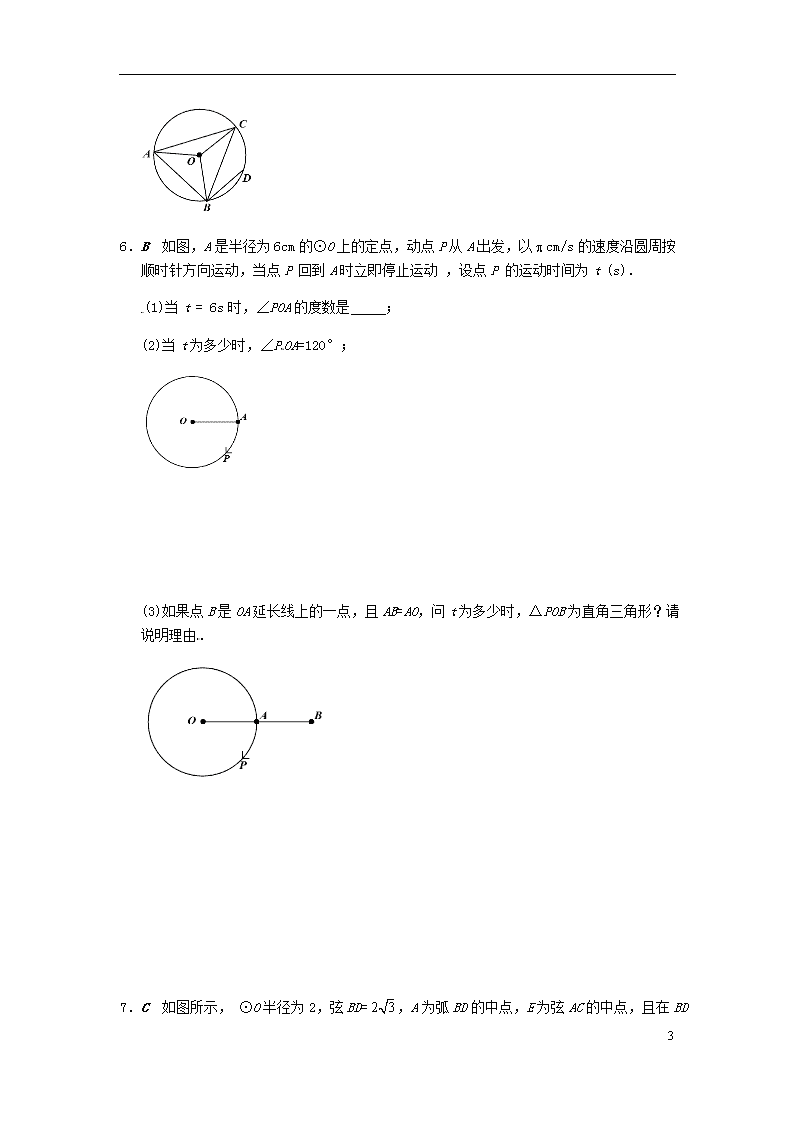
圆中三大基本定理(第2.1~2.4节复习)‎ ‎1．A 如图，CD是⊙O的直径，弦AB⊥CD于点E，连接AC，BC，下列结论中不一定正确的是( )．‎ A．AE=BE B．弧AD=弧BD C．OE = DE D．AC=BC ‎ ‎2．B 已知在以点O为圆心的两个同心圆，大圆的弦AB交小圆于点C，D．‎ ‎(1)求证：AC=BD；‎ ‎(2)若大圆的半径R =10，小圆的半径r =8，且圆O到直线AB的距离为6，求AC的长．‎ 8‎ ‎3．B 我们在园林游玩时，常见到如图所示的圆弧形的门.圆弧所在圆与地面BC的位置如下图所示，四边形ABCD是一个矩形，已知AB=米，BC=‎1米.‎ ‎(1)求圆弧形门最高点到地面的距离；‎ ‎(2)求弧AED的长 .‎ ‎4．A 如图在平台上用直径为‎100mm的两根圆钢棒嵌在大型工件的两侧，测量大的圆形工件的直径D，测得两根圆钢棒与地面的两个接触点之间的距离为‎400mm，则工件直径D(mm)用科学计数法可表示为( )‎ A. B. ‎ C.20000 D.‎ ‎5．A 如图，△ABC是⊙O的内接三角形，点D是弧BC的中点，已知∠AOB=98°，∠COB=120°，则∠ABD的度数是 .‎ 8‎ ‎6．B 如图，A是半径为‎6cm的⊙O上的定点，动点P从A出发，以cm/s的速度沿圆周按顺时针方向运动，当点P 回到A时立即停止运动 ，设点P 的运动时间为t (s)．‎ ‎(1)当t = 6s时，∠POA的度数是 ；‎ ‎(2)当t为多少时，∠POA=120°；‎ ‎ (3)如果点B是OA延长线上的一点，且AB=AO，问t为多少时，△POB为直角三角形？请说明理由.‎ ‎7．C 如图所示， ⊙O半径为2，弦BD=，A为弧BD的中点，E为弦AC的中点，且在BD 8‎ 上，求四边形ABCD的面积.‎ ‎8．A 如图，线段AB是⊙O的直径，弦CD⊥AB，∠CAB=20°，则∠AOD等于( )‎ A.160° B.150° C.140° D.120°‎ ‎9．A 如图，⊙O是△ABC的外接圆，AB是⊙O的直径，D为⊙O上一点，OD⊥AC，垂足为点E，连接BD.‎ ‎(1)求证：BD平分∠ABC；‎ ‎(2)当∠ODB =30°时，求证：BC = OD.‎ 8‎ ‎10．A 已知：在△ABC中，以AC边为直径的⊙O交BC于点D，在劣弧AD上取一点E使∠EBC=∠DEC，延长BE依次交AC于点G，交⊙O于H.‎ ‎(1)求证：AC⊥BH；‎ ‎(2)若∠ABC=45°，⊙O的直径等于10，BD=8，求CE的长.‎ ‎11．B 如图，AD是⊙O的直径.‎ ‎(1)如图①，垂直于AD的两条弦B‎1C1，B‎2C2把圆周4等分，则∠B1的度数是 ，∠B2的度数是 ；‎ ‎(2)如图②，垂直于AD的三条弦B‎1C1，B‎2C2，B‎3C3把圆周6等分，则∠B1的度数是 ，∠B2的度数是 ，∠B3的度数是 ；‎ 8‎ ‎(3)如图③，垂直于AD的n条弦B‎1C1，B‎2C2，B‎3C3 … ，BnCn把圆周2n等分，请你用含n的代数式表示∠Bn的度数(只需直接写出答案).‎ ‎12．B 如图，在⊙O内有折线OABC，其中OA=8，AB=12，∠A=∠B=60°，则BC的长为______． ‎ ‎13．C 如图，AB为⊙O的直径，C为半圆的中点，D为弧AC上一点，延长AD至E，使AE=BD，连CE，求的值． ‎ ‎ ‎ ‎———————————————————‎ 8‎ 圆中三大基本定理(第2.1~2.4节复习)‎ ‎1．C．‎ ‎2．(1)证明：过点O作OM⊥AB，垂足为点M，‎ 那么根据垂径定理可知：CM=DM，AM=BM，‎ ‎∵AC=AM－CM，BD=BM－DM，‎ ‎∴AC=BD；‎ ‎(2)．‎ ‎3．2；.‎ ‎4．D．‎ ‎5．101°．‎ ‎6．180°；4s或8s；2s、3s、9s、10s．‎ ‎7．．‎ ‎8．C．‎ ‎9．(1)∵AB是⊙O的直径，‎ ‎∴∠C=90°，‎ ‎∵OD⊥AC，垂足为点E，‎ ‎∴∠OEA=90°，‎ ‎∴BC∥OD，‎ ‎∴∠ODB=∠CBD，‎ ‎∵OD=OB，‎ ‎∴∠ODB=∠OBD，‎ ‎∴∠CBD=∠OBD，即BD平分∠ABC；‎ ‎(2)∵∠ODB =30°，‎ 由(1)可得∠CBD=∠OBD=30°，‎ ‎∴∠A=30°，‎ ‎∴Rt△ABC中，BC=AB，即BC=OD．‎ ‎10．(1)证明：连结AD，与BH交于点F，‎ ‎∵AC为⊙O的直径，‎ ‎∴∠ADB=90°，‎ ‎∵∠DEC和∠DAC都是弧CD所对的圆周角，‎ ‎∴∠DEC=∠DAC，‎ ‎∵∠EBC=∠DEC，‎ 8‎ ‎∴∠EBC=∠DAC，‎ 在△BDF和△AGF中，‎ ‎∵∠FBD=∠FAG，∠BFD=∠AFG，‎ ‎∴∠BDF=∠AGF，‎ ‎∴∠AGF=90°，即AC⊥BH；‎ ‎(2).‎ ‎11．22.5°，67.5°；15°，45°，75°；90°－°．‎ ‎12．20．‎ ‎13．．‎ 8‎