2021年九年级中考数学一轮复习精练+热考题型：几何变换综合题（五）

2021年九年级中考数学一轮复习精练+热考题型：几何变换综合题（五）

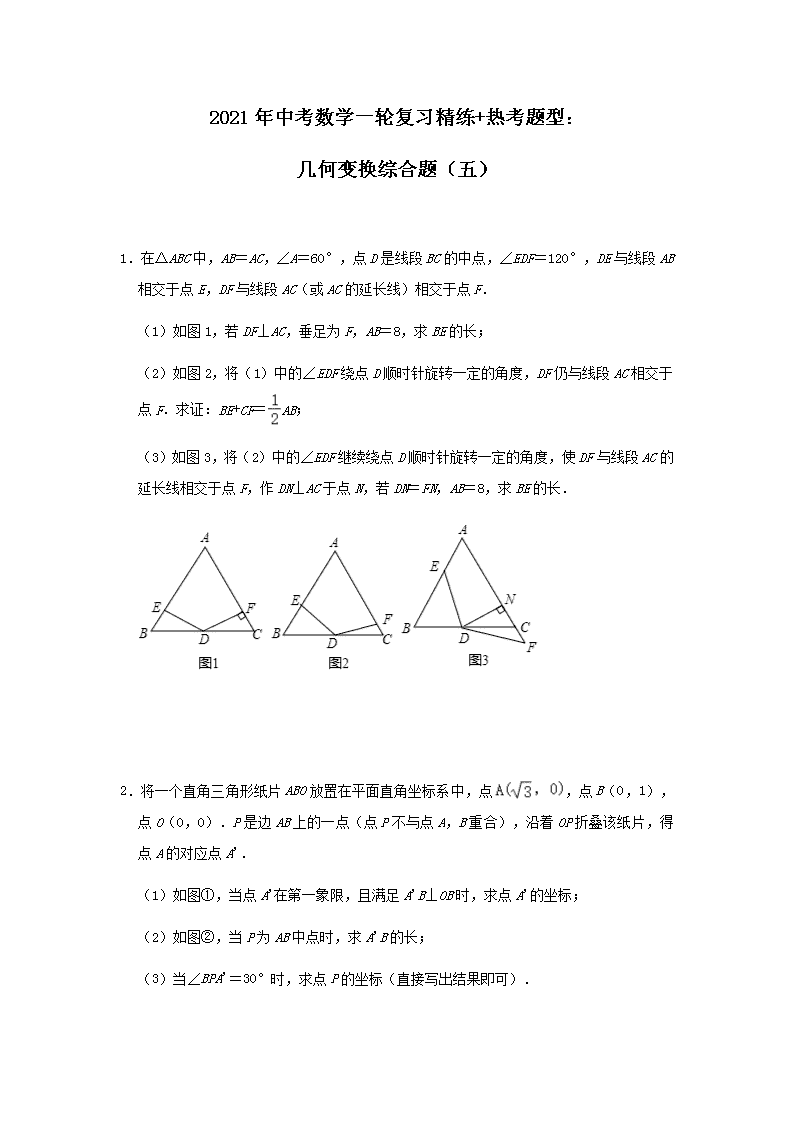
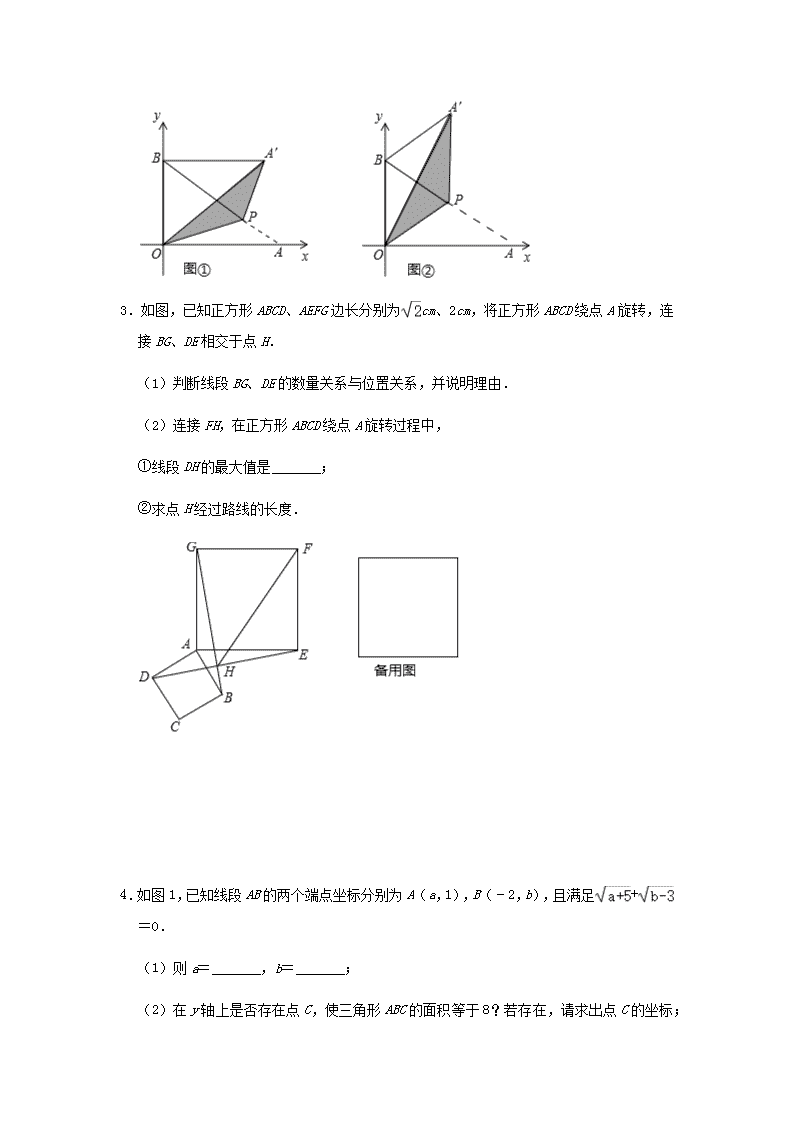
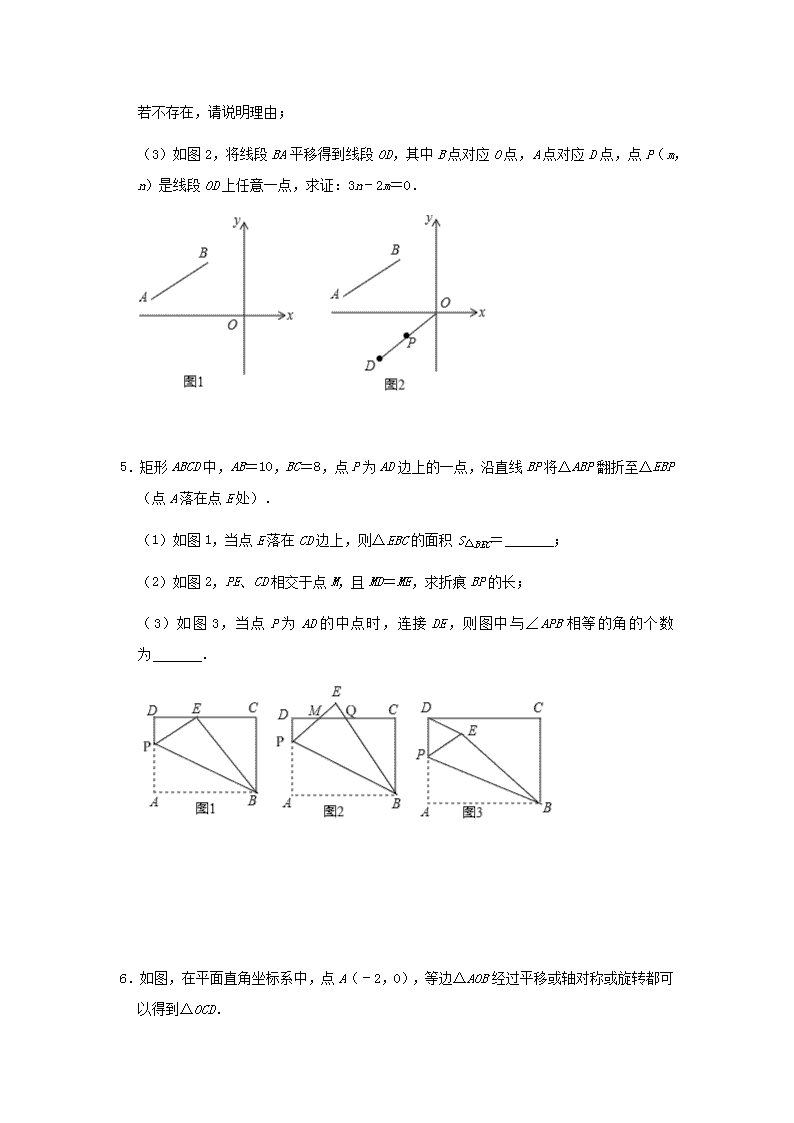
2021 年中考数学一轮复习精练+热考题型： 几何变换综合题（五） 1．在△ABC 中，AB＝AC，∠A＝60°，点 D 是线段 BC 的中点，∠EDF＝120°，DE 与线 段 AB 相交于点 E，DF 与线段 AC（或 AC 的延长线）相交于点 F． （1）如图 1，若 DF⊥AC，垂足为 F，AB＝8，求 BE 的长； （2）如图 2，将（1）中的∠EDF 绕点 D 顺时针旋转一定的角度，DF 仍与线段 AC 相交 于点 F．求证：BE+CF＝ AB； （3）如图 3，将（2）中的∠EDF 继续绕点 D 顺时针旋转一定的角度，使 DF 与线段 AC 的延长线相交于点 F，作 DN⊥AC 于点 N，若 DN＝FN，AB＝8，求 BE 的长． 2．将一个直角三角形纸片 ABO 放置在平面直角坐标系中，点 ，点 B（0，1）， 点 O（0，0）．P 是边 AB 上的一点（点 P 不与点 A，B 重合），沿着 OP 折叠该纸片， 得点 A 的对应点 A'． （1）如图①，当点 A'在第一象限，且满足 A'B⊥OB 时，求点 A'的坐标； （2）如图②，当 P 为 AB 中点时，求 A'B 的长； （3）当∠BPA'＝30°时，求点 P 的坐标（直接写出结果即可）． 3．如图，已知正方形 ABCD、AEFG 边长分别为 cm、2cm，将正方形 ABCD 绕点 A 旋转， 连接 BG、DE 相交于点 H． （1）判断线段 BG、DE 的数量关系与位置关系，并说明理由． （2）连接 FH，在正方形 ABCD 绕点 A 旋转过程中， ①线段 DH 的最大值是 ； ②求点 H 经过路线的长度． 4．如图 1，已知线段 AB 的两个端点坐标分别为 A（a，1），B（﹣2，b），且满足 + ＝0． （1）则 a＝ ，b＝ ； （2）在 y 轴上是否存在点 C，使三角形 ABC 的面积等于 8？若存在，请求出点 C 的坐标； 若不存在，请说明理由； （3）如图 2，将线段 BA 平移得到线段 OD，其中 B 点对应 O 点，A 点对应 D 点，点 P （m，n）是线段 OD 上任意一点，求证：3n﹣2m＝0． 5．矩形 ABCD 中，AB＝10，BC＝8，点 P 为 AD 边上的一点，沿直线 BP 将△ABP 翻折至 △EBP（点 A 落在点 E 处）． （1）如图 1，当点 E 落在 CD 边上，则△EBC 的面积 S△BEC＝ ； （2）如图 2，PE、CD 相交于点 M，且 MD＝ME，求折痕 BP 的长； （3）如图 3，当点P为AD 的中点时，连接 DE，则图中与∠APB 相等的角的个数为 ． 6．如图，在平面直角坐标系中，点 A（﹣2，0），等边△AOB 经过平移或轴对称或旋转都 可以得到△OCD． （1）填空： ①△AOB 沿 x 轴向右平移得到△OCD，则平移的距离是 个单位长度； ②△AOB 与△OCD 关于某直线对称，则对称轴是 ； ③△AOB 绕原点 O 顺时针旋转得到△OCD，则旋转角度可以是 度； （2）连接 AD，请探索 AD 与 CD 的位置关系． 7．如图，矩形 ABCD 中，P 为 AD 上一点．将△ABP 沿 BP 翻折至△EBP，点 A 与点 E 重 合： （1）如图 1，AB＝10，BC＝6，点 E 落在 CD 边上，求 AP 的长； （2）如图 2，若 AB＝8，BC＝6，PE 与 CD 相交于点 O，且 OE＝OD，求 AP 的长； （3）如图 3，若 AB＝4．BC＝6，点 P 是 AD 的中点，求 DE 的长． 8．在 Rt△ABC 中，∠ACB＝90°，AC＝BC，CD 为 AB 边上的中线．在 Rt△AEF 中，∠ AEF＝90°，AE＝EF，AF＜AC．连接 BF，M，N 分别为线段 AF，BF 的中点，连接 MN． （1）如图 1，点 F 在△ABC 内，求证：CD＝MN； （2）如图 2，点 F 在△ABC 外，依题意补全图 2，连接 CN，EN，判断 CN 与 EN 的数 量关系与位置关系，并加以证明； （3）将图 1 中的△AEF 绕点 A 旋转，若 AC＝a，AF＝b（b＜a），直接写出 EN 的最大 值与最小值． 9．在△ABC 中，∠B＝45°，∠C＝30°． （1）如图 1，若 AB＝5 ，求 BC 的长； （2）点 D 是 BC 边上一点，连接 AD，将线段 AD 绕点 A 逆时针旋转 90°，得到线段 AE． ①如图 2，当点 E 在 AC 边上时，求证：CE＝2BD； ②如图 3，当点 E 在 AC 的垂直平分线上时，直接写出 的值． 10．已知等边三角形△ABC，点 D 和点 B 关于直线 AC 轴对称．点 M（不同于点 A 和点 C ） 在射线 CA 上，线段 DM 的垂直平分线交直线 BC 于点 N （1）如图 1，过点 D 作 DE⊥BC，交 BC 的延长线于 E．CE＝5，求 BC 的长； （2）如图 2，若点 M 在线段 AC 上，求证：△DMN 为等边三角形； （3）连接 CD，BM，若 ＝3，直接写出 ＝ 参考答案 1．解：（1）如图 1， ∵AB＝AC，∠A＝60°， ∴△ABC 是等边三角形， ∴∠B＝∠C＝60°，BC＝AC＝AB＝4． ∵点 D 是线段 BC 的中点， ∴BD＝DC＝ BC＝4， ∵DF⊥AC，即∠AFD＝90°， ∴∠AED＝360°﹣60°﹣90°﹣120°＝90°， ∴∠BED＝90°， ∴BE＝BD×cos∠B＝4×cos60°＝4× ＝2； （2）过点 D 作 DM⊥AB 于 M，作 DN⊥AC 于 N，如图 2， 则有∠AMD＝∠BMD＝∠AND＝∠CND＝90°． ∵∠A＝60°，∴∠MDN＝360°﹣60°﹣90°﹣90°＝120°． ∵∠EDF＝120°，∴∠MDE＝∠NDF． 在△MBD 和△NCD 中， ， ∴△MBD≌△NCD， ∴BM＝CN，DM＝DN． 在△EMD 和△FND 中， ， ∴△EMD≌△FND， ∴EM＝FN， ∴BE+CF＝BM+EM+CF＝BM+FN+CF＝BM+CN ＝2BM＝2BD×cos60°＝BD＝ BC＝ AB； （3）过点 D 作 DM⊥AB 于 M，如图 3． 同（1）可得：∠B＝∠ACD＝60°． 同（2）可得：BM＝CN，DM＝DN，EM＝FN． ∵DN＝FN， ∴DM＝DN＝FN＝EM， ∴BE+CF＝BM+EM+CF＝CN+DM+CF＝NF+DM＝2DM＝2BD×sin60°＝ BC＝ AB， ∴（2）中的结论不成立； ∵AB＝8， ∴BD＝4， ∵BE+CF＝BE+NF﹣CN＝BE+DM﹣BM＝BE+ BD﹣ BD＝ AB， ∴BE＝2 +2． 2．解：（1）∵点 ，点 B（0，1）， ∴OA＝ ，OB＝1， 由折叠的性质得：OA'＝OA＝ ， ∵A'B⊥OB， ∴∠A'BO＝90°， 在 Rt△A'OB 中，A'B＝ ＝ ， ∴点 A'的坐标为（ ，1）； （2）在 Rt△ABO 中，OA＝ ，OB＝1， ∴AB＝ ＝2， ∵P 是 AB 的中点， ∴AP＝BP＝1，OP＝ AB＝1， ∴OB＝OP＝BP ∴△BOP 是等边三角形， ∴∠BOP＝∠BPO＝60°， ∴∠OPA＝180°﹣∠BPO＝120°， 由折叠的性质得：∠OPA'＝∠OPA＝120°，PA'＝PA＝1， ∴∠BOP+∠OPA'＝180°， ∴OB∥PA'， 又∵OB＝PA'＝1， ∴四边形 OPA'B 是平行四边形， ∴A'B＝OP＝1； （3）设 P（x，y），分两种情况： ①∵∠BPA'＝30°， ∴∠APA'＝150°， 连接 AA′，延长 OP 交 AA′于 E，如图③所示： 则∠APE＝75°， ∴∠OPB＝75°， ∵OA＝ ，OB＝1， ∴AB＝ ＝ ＝2， ∴∠BAO＝30°，∠OBA＝60°， ∵∠BPA'＝30°， ∴∠BA′P＝30°，∠OPA′＝105°， ∴∠A′OP＝180°﹣30°﹣105°＝45°， ∴点 A'在 y 轴上， ∴∠A'OP＝∠AOP＝ ∠AOB＝45°， ∴点 P 在∠AOB 的平分线上， 设直线 AB 的解析式为 y＝kx+b， 把点 ，点 B（0，1）代入得： ， 解得： ， ∴直线 AB 的解析式为 y＝﹣ x+1， ∵P（x，y）， ∴x＝﹣ x+1， 解得：x＝ ， ∴P（ ， ）； ②如图④所示： 由折叠的性质得：∠A'＝∠A＝30°，OA'＝OA， ∵∠BPA'＝30°， ∴∠A'＝∠A＝∠BPA'， ∴OA'∥AP，PA'∥OA， ∴四边形 OAPA'是菱形， ∴PA＝OA＝ ，作 PM⊥OA 于 M，如图④所示： ∵∠A＝30°， ∴PM＝ PA＝ ， 把 y＝ 代入 y＝﹣ x+1 得： ＝﹣ x+1， 解得：x＝ ， ∴P（ ， ）； 综上所述：当∠BPA'＝30°时，点 P 的坐标为（ ， ）或（ ， ）． 3．解：DE＝BG，DE⊥BG， 理由：如图， ∵四边形 ABCD 和四边形 AEFG 是正方形， ∴AD＝AB，AE＝AG，∠DAB＝∠EAG＝90°， ∴∠DAE＝∠BAG， 在△ADE 和△ABG 中， ， ∴△ADE≌△ABG， ∴DE＝BG，∠AED＝∠AGB， ∵∠AGB+∠AMG＝90°， ∴∠AED+∠AMG＝90°， ∵∠AMG＝∠EMH， ∴∠AED+∠EMH＝90°， ∴∠EHG＝90°， ∴DE⊥BG； 即：DE＝BG，DE⊥BG； （2）①由（1）知，∠EHG＝90°＝∠C， ∴点 H 是正方形 ABCD 的外接圆上， ∴DH 是正方形 ABCD 的外接圆的弦， ∴DH 最大就是正方形 ABCD 的外接圆的直径 BD＝2cm； 故答案为 2cm； ②如图 2， 作出正方形 AEFG 的外接圆， 连接 OC'，OC，FC，FC'， 由（1）知，∠EHG＝90°＝∠EFG， ∴点 H 在正方形 AEFG 的外接圆⊙O 上， 点 H 的运动轨迹是如图 2 所示的 这段弧，（即：点 D，B，E 在同一条线上时， 和点 G，D'，B'在同一条线上时，） ∴当∠AGH 越大， 越长， 即：GH⊥AB 时，∠AGH 最大， ∵正方形 AEFG 的边长是 2， ∴OA＝OB＝ ， ∵AB＝ ， ∴OA＝OB＝AB， ∴∠AOB＝60°， 同理：∠AOD'＝60°， ∴∠BOD'＝∠AOB+∠AOD'＝120° ∴点 H 经过路线的长度为 •2π• ＝ π（cm）． 4．解：（1）∵ + ＝0． ∴a+5＝0，b﹣3＝0， ∴a＝﹣5，b＝3， 故答案：﹣5，3； （2）存在，理由：如图 1， 延长 AB 交 y 轴于 E， 设 C（0，c）， ∵a＝﹣5，b＝3， ∴A（﹣5，1），B（﹣2，3）， ∴AB 的解析式为 y＝ x+ （﹣5≤x≤﹣2）， ∴E（0， ）， ∴CE＝|c﹣ |， ∵S△ABC＝8， ∴S△ABC＝S△ACE﹣S△BCE＝ CE•|xA|﹣ CE•|xB|＝ CE•（|xA|﹣|xB|）＝ ×|c﹣ | ×（5﹣2）＝8， ∴|c﹣ |＝ ， ∴c＝ 或 c＝﹣ ， ∴C（0， ）或（0，﹣1）； （3）∵将线段 BA 平移得到线段 OD， ∴OD 的解析式为 y＝ x（﹣3≤x≤0）， ∵点 P（m，n）在线段 OD 上， ∴n＝ m， ∴3n﹣2m＝0． 5．解：（1）由折叠知，BE＝AB＝10， 在 Rt△BCE 中，BC＝8，根据勾股定理得，CE＝6， ∴S△BCE＝ CE•BC＝24， 故答案为 24， （2）如图 2， 当 MD＝ME 时，设 BE 交 DC 与点 Q， 在△DPM 和△EQM 中， ， ∴△DPM≌△EQM ∴DP＝EQ DQ＝EP， 设 AP＝x，则 DP＝8﹣x＝EQ DQ＝EP＝AP＝x ∴CQ＝10﹣x BQ＝2+x， 在 Rt△CBQ 中，由勾股定理得：64+（10﹣x）2＝（x+2）2， 解得 x＝ ，即 AP＝ ， 在 Rt△ABP 中，由勾股定理得：BP＝ ， （3）由折叠知，∠BPE＝∠APB，AP＝PE， ∵点 P 是 AD 中点， ∴AP＝DP， ∴PD＝PE， ∴∠PDE＝∠PED， ∵2∠PDE+∠DPE＝180°，2∠APB+∠DPE＝180°， ∴∠PDE＝∠APB， ∴∠PDE＝∠PED＝∠BPE＝∠APB， ∵∠APB+∠ABP＝90°，∠PBC+∠ABP＝90°， ∴∠APB＝∠PBC 故答案为 4． 6．解：（1）△AOB 沿 x 轴向右平移得到△OCD，根据 AO＝2 可知，平移的距离是 2 个单 位长度； △AOB 与△COD 关于直线对称，根据线段 AC 被 y 轴垂直平分可知，对称轴是 y 轴； △AOB 绕原点 O 顺时针旋转得到△DOC，根据∠BOC＝180°﹣∠AOB＝120°可知，旋 转角度可以是 120°； 故答案为：2；y 轴；120 （2）由 AO＝DO，∠COD＝60°可得，∠OAD＝∠ODA＝30°， ∴∠ADC＝30°+60°＝90°， ∴AD⊥CD． 7．解：（1）如图 1，由折叠可得，AP＝EP，AB＝EB＝10， Rt△BCE 中，由勾股定理可得，CE＝8， ∴DE＝CD﹣CE＝2， 设 AP＝EP＝x，则 PD＝6﹣x， ∵Rt△DEP 中，DE2+DP2＝PE2， ∴22+（6﹣x）2＝x2， 解得 x＝ ， ∴AP 的长为 ； （2）如图 2，∵四边形 ABCD 是矩形， ∴∠D＝∠A＝∠C＝90°，AD＝BC＝6，CD＝AB＝8， 根据题意得：△ABP≌△EBP， ∴EP＝AP，∠E＝∠A＝90°，BE＝AB＝8， 在△ODP 和△OEG 中， ， ∴△ODP≌△OEG（ASA）， ∴OP＝OG，PD＝GE， ∴DG＝EP， 设 AP＝EP＝x，则 PD＝GE＝6﹣x，DG＝x， ∴CG＝8﹣x，BG＝8﹣（6﹣x）＝2+x， 根据勾股定理得：BC2+CG2＝BG2， 即 62+（8﹣x）2＝（x+2）2， 解得 x＝4.8， ∴AP＝4.8； （3）解法一：如图 3，取 DE 的中点 F，连接 PF，则 当点 P 是 AD 的中点时，DP＝AP＝EP＝3， ∴PF⊥DE， ∴∠PFE＝∠BEP＝90°， 由折叠可得，∠BPE＝ ∠APE＝∠PEF，BE＝AB＝4， ∴△PEF∽△BPE， ∴ ，即 ， ∴PF＝ EF， 又∵EF2+PF2＝PE2， ∴EF2+（ EF）2＝32， 解得 EF＝ ， ∴DE＝ ； 解法二：如图 3，过 E 作 GF∥AB，交 AD 于 G，交 BC 于 F，则∠PGE＝∠EFB＝90°， GF＝AB＝4， 设 GE＝x，则 EF＝4﹣x， 由折叠可得，∠BEP＝∠A＝90°，AB＝BE＝4，PE＝AP＝ AD＝3， ∴∠PEG＝∠EBF， ∴△PEG∽△EBF， ∴ ＝ ，即 ＝ ， ∴PG＝ （4﹣x）， ∵Rt△EGP 中，GE2+PG2＝PE2， ∴x2+[ （4﹣x）]2＝32， 解得 x1＝0（舍去），x2＝ ， ∴GE＝ ，GD＝DP﹣PG＝3﹣ （4﹣ ）＝ ， ∴Rt△DEG 中，DE＝ ＝ ＝ ， ∴DE 的长为 ． 8．解：（1）证明：在 Rt△ABC 中， ∵CD 是斜边 AB 上的中线． ∴CD＝ AB． 在△ABF 中，点 M，N 分别是边 AF，BF 的中点， ∴MN＝ AB， ∴CD＝MN． （2）答：CN 与 EN 的数量关系 CN＝EN， CN 与 EN 的位置关系 CN⊥EN． 证明：连接 EM，DN，如图． 与（1）同理可得 CD＝MN，EM＝DN． 在 Rt△ABC 中，CD 是斜边 AB 边上的中线， ∴CD⊥AB． 在△ABF 中，同理可证 EM⊥AF． ∴∠EMF＝∠CDB＝90°． ∵D，M，N 分别为边 AB，AF，BF 的中点， ∴DN∥AF，MN∥AB． ∴∠FMN＝∠MND，∠BDN＝∠MND． ∴∠FMN＝∠BDN． ∴∠EMF+∠FMN＝∠CDB+∠BCN． ∴∠EMN＝∠NDC． ∴△EMN≌△DNC． ∴CN＝EN，∠1＝∠2． ∵∠1+∠3+∠EMN＝180°， ∴∠2+∠3+∠FMN＝90°． ∴∠2+∠3+∠DNM＝90°， 即∠CNE＝90°． ∴CN⊥EN． （3）点 N 是以点 D 为圆心， 为半径的圆上， 在 Rt△ABC 中，AC＝BC＝a， ∴AB＝ a， ∵CD 为 AB 边上的中线． ∴CD＝ AB＝ ， ∴CN 最大＝CD+ ＝ ，CN 最小＝CD﹣ ＝ 由（2）知，EN＝CN， ∴EN 最大＝ ，EN 最小＝ 即：EN 的最大值为 ，最小值为 ． 9．解：（1）如图 1，过点 A 作 AH⊥BC 于 H，则∠AHB＝∠AHC＝90°， 在 Rt△AHB 中，∵AB＝5 ，∠B＝45°， ∴BH＝ABcosB＝5，AH＝ABsinB＝5， 在 Rt△AHC 中，∵∠C＝30°， ∴AC＝2AH＝10，CH＝ACcosC＝5 ， ∴BC＝BH+CH＝5+5 ； （2）①证明：如图 2，过点 A 作 AP⊥AB 交 BC 于 P，连接 PE，则∠BAP＝90°，∠APB ＝45°， 由旋转可得，AD＝AE，∠DAE＝90°， ∴∠BAP＝90°＝∠DAE， ∴∠BAD＝∠PAE， ∵∠B＝∠APB＝45°， ∴AB＝AP， 在△ABD 和△APE 中， ， ∴△ABD≌△APE， ∴BD＝PE，∠B＝∠APE＝45°， ∴∠EPB＝∠EPC＝90°， ∵∠C＝30°， ∴CE＝2PE， ∴CE＝2BD； ②如图 3，作 AH⊥BC 于 H，AC 的垂直平分线交 AC 于 P，交 BC 于 M，则 AP＝PC， 在 Rt△AHC 中，∵∠ACH＝30°， ∴AC＝2AH， ∴AH＝AP， 在 Rt△AHD 和 Rt△APE 中， ， ∴△AHD≌△APE（HL）， ∴∠DAH＝∠EAP， ∵EM⊥AC，PA＝PC， ∴MA＝MC， ∴∠MAC＝∠MCA＝∠MAH＝30°， ∴∠DAM＝∠EAM＝ ∠DAE＝45°， ∴∠DAH＝∠EAP＝15°， ∴∠BAD＝∠BAH﹣∠DAH＝30°， 如图 3，作 DK⊥AB 于 K， 设 BK＝DK＝a，则 AK＝ a，AD＝2a， ∴ ＝ ＝ ， ∵AE＝CE＝AD， ∴ ＝ ． 10．解：（1）如图 1，连接 CD， ∵△ABC 是等边三角形，点 D 和点 B 关于直线 AC 轴对称， ∴BC＝DC，∠ACB＝∠ACD＝60°， ∴∠DCE＝60°， ∵DE⊥CE，CE＝5， ∴∠CDE＝30°， ∴CD＝2CE＝10， ∴BC＝10； （2）如图 2，过点 N 作 NG⊥CD 于 G，作 NH⊥AC 于 H，则∠H＝∠DGN＝90°， ∵△ABC 是等边三角形，点 D 和点 B 关于直线 AC 轴对称， ∴∠1＝∠2＝60°， ∴∠3＝60°＝∠4，即 NC 平分∠GCH， ∴NG＝NH， ∵线段 DM 的垂直平分线交直线 BC 于点 N， ∴NM＝ND， 在 Rt△MNH 和 Rt△DNG 中， ， ∴Rt△MNH≌Rt△DNG（HL）， ∴∠CMQ＝∠NDQ， 又∵∠MQC＝∠DQN， ∴∠2＝∠5＝60°， ∵NM＝ND， ∴△DMN 为等边三角形； （3）①如图 3，当点 M 在线段 AC 上时，连接 AD，BD，则 BD⊥AC，BP＝DP， ∵△ACD 和△MND 都是等边三角形， ∴AD＝CD，∠ADM＝∠CDN，MD＝ND， ∴△ADM≌△CDN， ∴AM＝CN， ∵ ＝3， ∴ ＝ ， ∴ ＝ ， ∴ ＝ ，即 ＝ ， ∴ ＝ ， ∴ ＝ ； ②如图 4，当点 M 在 CA 延长线上时，连接 AD， 同理可得，△ADM≌△CDN， ∴AM＝CN， ∵ ＝3， ∴ ＝ ， ∴ ＝ ，即 ＝ ， ∴BN＝CN， ∴ ＝1． 综上所述， ＝ 或 1． 故答案为： 或 1．