2021年中考数学专题复习 专题22 三角形中位线定理应用问题（学生版）

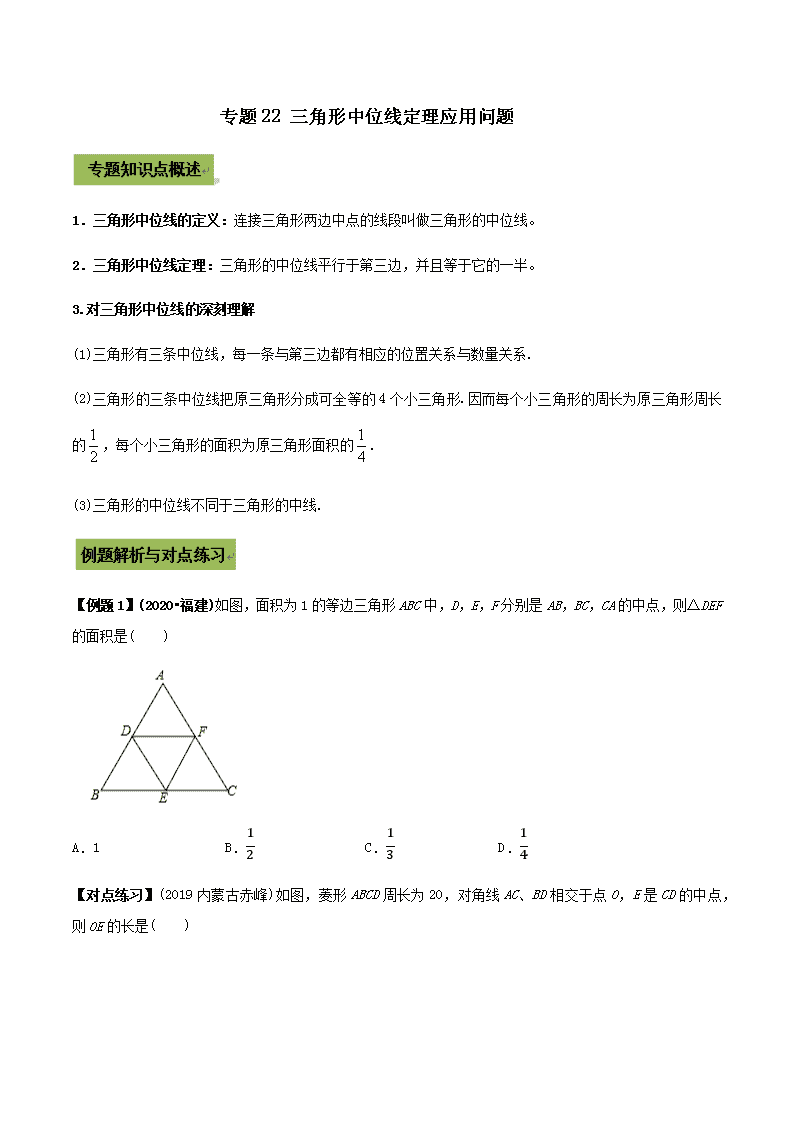
2021年中考数学专题复习 专题22 三角形中位线定理应用问题（学生版）

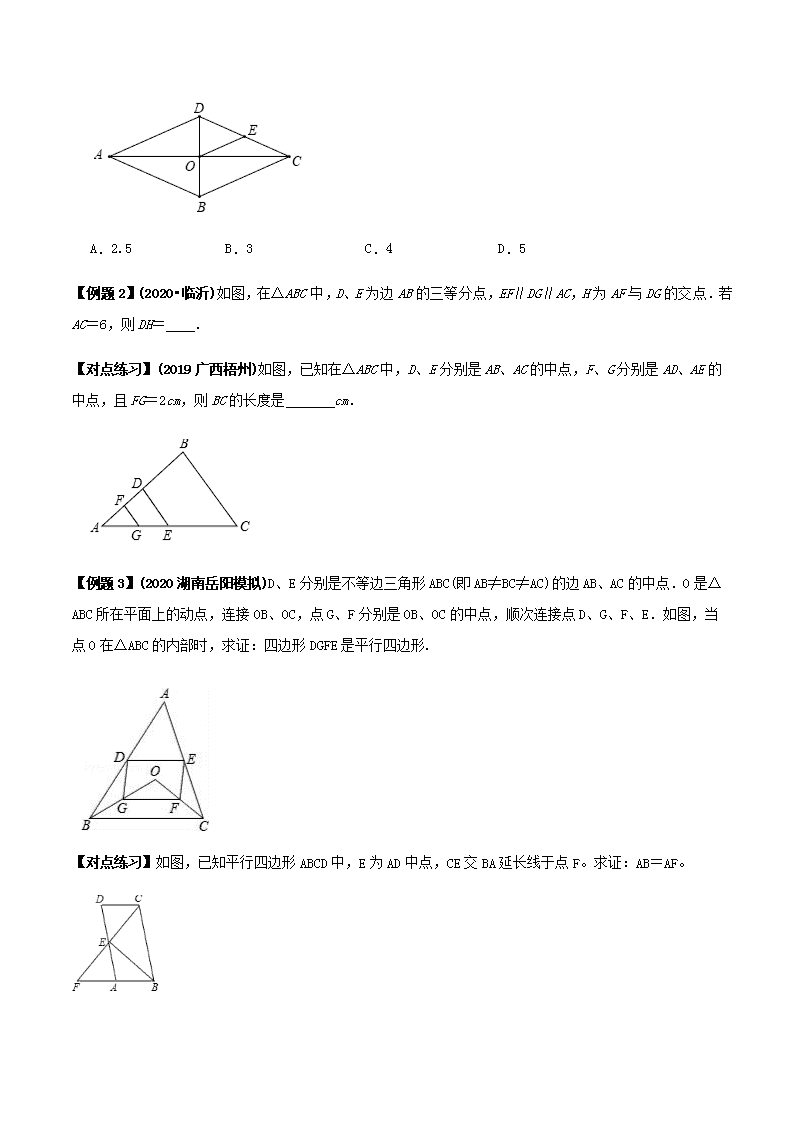
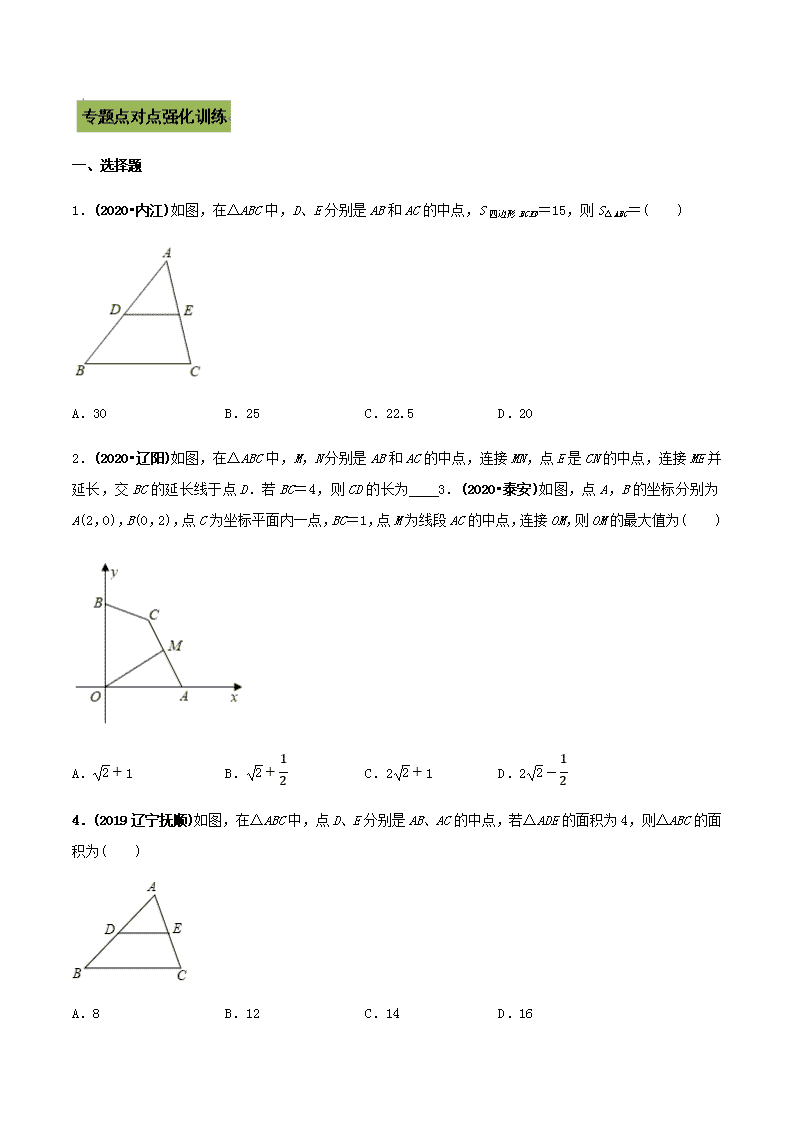
专题 22 三角形中位线定理应用问题 1．三角形中位线的定义：连接三角形两边中点的线段叫做三角形的中位线。 2．三角形中位线定理：三角形的中位线平行于第三边，并且等于它的一半。 3.对三角形中位线的深刻理解 (1)三角形有三条中位线，每一条与第三边都有相应的位置关系与数量关系. (2)三角形的三条中位线把原三角形分成可全等的 4 个小三角形.因而每个小三角形的周长为原三角形周长 的 1 2 ，每个小三角形的面积为原三角形面积的 1 4 . (3)三角形的中位线不同于三角形的中线. 【例题 1】(2020•福建)如图，面积为 1 的等边三角形 ABC 中，D，E，F 分别是 AB，BC，CA 的中点，则△DEF 的面积是( ) A．1 B． C． D． 【对点练习】(2019 内蒙古赤峰)如图，菱形 ABCD 周长为 20，对角线 AC、BD 相交于点 O，E 是 CD 的中点， 则 OE 的长是( ) A．2.5 B．3 C．4 D．5 【例题 2】(2020•临沂)如图，在△ABC 中，D、E 为边 AB 的三等分点，EF∥DG∥AC，H 为 AF 与 DG 的交点．若 AC＝6，则 DH＝ ． 【对点练习】(2019 广西梧州)如图，已知在△ABC 中，D、E 分别是 AB、AC 的中点，F、G 分别是 AD、AE 的 中点，且 FG＝2cm，则 BC 的长度是 cm． 【例题 3】(2020 湖南岳阳模拟)D、E 分别是不等边三角形 ABC(即 AB≠BC≠AC)的边 AB、AC 的中点．O 是△ ABC 所在平面上的动点，连接 OB、OC，点 G、F 分别是 OB、OC 的中点，顺次连接点 D、G、F、E．如图，当 点 O 在△ABC 的内部时，求证：四边形 DGFE 是平行四边形. 【对点练习】如图，已知平行四边形 ABCD 中，E 为 AD 中点，CE 交 BA 延长线于点 F。求证：AB＝AF。 一、选择题 1．(2020•内江)如图，在△ABC 中，D、E 分别是 AB 和 AC 的中点，S 四边形 BCED＝15，则 S△ABC＝( ) A．30 B．25 C．22.5 D．20 2．(2020•辽阳)如图，在△ABC 中，M，N 分别是 AB 和 AC 的中点，连接 MN，点 E 是 CN 的中点，连接 ME 并 延长，交 BC 的延长线于点 D．若 BC＝4，则 CD 的长为 3．(2020•泰安)如图，点 A，B 的坐标分别为 A(2， 0)，B(0，2)，点 C 为坐标平面内一点，BC＝1，点 M 为线段 AC 的中点，连接 OM，则 OM 的最大值为( ) A． 1 B． C．2 1 D．2 4．(2019 辽宁抚顺)如图，在△ABC 中，点 D、E 分别是 AB、AC 的中点，若△ADE 的面积为 4，则△ABC 的面 积为( ) A．8 B．12 C．14 D．16 5．(2019 湖北襄阳)如图，AD 是⊙O 的直径，BC 是弦，四边形 OBCD 是平行四边形，AC 与 OB 相交于点 P， 下列结论错误的是( ) A．AP＝2OP B．CD＝2OP C．OB⊥AC D．AC 平分 OB 二、填空题 6．(2020 铜仁市模拟)如图，∠ACB=9O°，D 为 AB 中点，连接 DC 并延长到点 E，使 CE= CD，过点 B 作 BF ∥DE 交 AE 的延长线于点 F．若 BF=10，则 AB 的长为 ． 三、解答题 7.如图，在  ABCD 中，点 E 是 AD 的中点，BE 的延长线与 CD 的延长线相交于点 F (1)求证：△ABE≌△DFE； (2)试连结 BD、AF，判断四边形 ABDF 的形状，并证明你的结论．