九年级数学上册第23章图形的相似23-3相似三角形23-3-3相似三角形的性质教案新版华东师大版

九年级数学上册第23章图形的相似23-3相似三角形23-3-3相似三角形的性质教案新版华东师大版

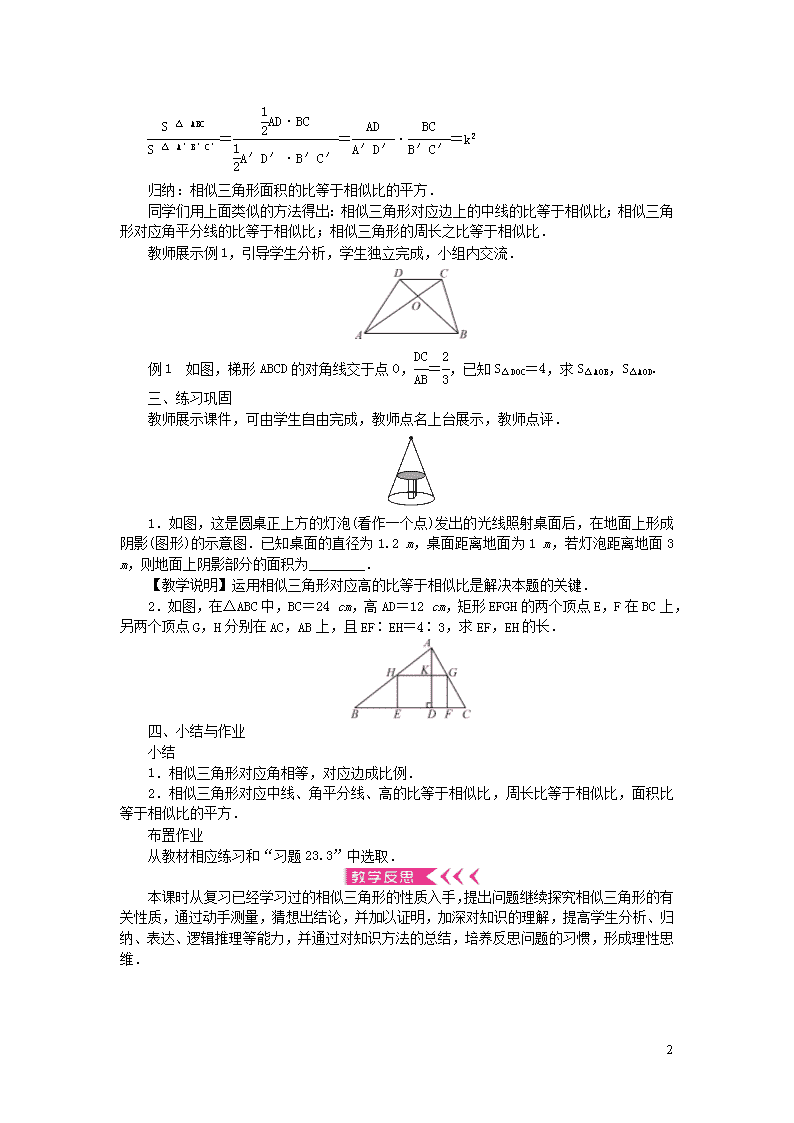
‎ ‎ ‎23．3.3　相似三角形的性质 会说出相似三角形的性质：对应角相等，对应边成比例，对应中线、角平分线、高的比等于相似比，周长比等于相似比，面积比等于相似比的平方．‎ 重点 ‎1．相似三角形中的对应线段比值的推导．‎ ‎2．相似多边形的周长比、面积比与相似比关系的推导．‎ ‎3．运用相似三角形的性质解决实际问题．‎ 难点 相似三角形性质的灵活运用，相似三角形周长比、面积比与相似比关系的推导及运用．‎ 一、情境引入 复习：‎ ‎1．判定两个三角形相似的简便方法有哪些？‎ ‎2．在△ABC与△A′B′C′中，AB＝10 cm，AC＝6 cm，BC＝8 cm，A′B′＝5 cm，A′C′＝3 cm，B′C′＝4 cm，这两个三角形相似吗？说明理由．如果相似，它们的相似比是多少？‎ 二、探究新知 教师结合上述第2题，引导学生探究：‎ 上述两个三角形是相似的，它们对应边的比就是相似比，△ABC∽△A′B′C′，相似比为＝2.‎ 相似的两个三角形，它们的对应角相等，对应边会成比例，除此之处，还会得出什么结果呢？‎ 一个三角形内有三条主要线段——高线、中线、角平分线，如果两个三角形相似，那么这些对应的线段有什么关系呢？我们先探索一下它们的对应高之间的关系．‎ 同学们画出上述的两个三角形，作对应边BC和B′C′边上的高，用刻度尺量一量AD与A′D′的长，等于多少呢？与它们的相似比相等吗？得出结论：相似三角形对应高的比等于相似比．我们能否用推理的方法来说明这个结论呢？‎ ‎△ABD和△A′B′D′都是直角三角形，且∠B＝∠B′.‎ ‎∴△ABD∽△A′B′D′，∴＝＝k.‎ 接下来，教师再提出问题让学生归纳，并引导学生通过演绎推理来证明．‎ 思考：相似三角形面积的比与相似比有什么关系？‎ 2‎ ＝＝·＝k2‎ 归纳：相似三角形面积的比等于相似比的平方．‎ 同学们用上面类似的方法得出：相似三角形对应边上的中线的比等于相似比；相似三角形对应角平分线的比等于相似比；相似三角形的周长之比等于相似比．‎ 教师展示例1，引导学生分析，学生独立完成，小组内交流．‎ 例1　如图，梯形ABCD的对角线交于点O，＝，已知S△DOC＝4，求S△AOB，S△AOD.‎ 三、练习巩固 教师展示课件，可由学生自由完成，教师点名上台展示，教师点评．‎ ‎1．如图，这是圆桌正上方的灯泡(看作一个点)发出的光线照射桌面后，在地面上形成阴影(图形)的示意图．已知桌面的直径为1.2 m，桌面距离地面为1 m，若灯泡距离地面3 m，则地面上阴影部分的面积为________．‎ ‎【教学说明】运用相似三角形对应高的比等于相似比是解决本题的关键．‎ ‎2．如图，在△ABC中，BC＝24 cm，高AD＝12 cm，矩形EFGH的两个顶点E，F在BC上，另两个顶点G，H分别在AC，AB上，且EF∶EH＝4∶3，求EF，EH的长．‎ 四、小结与作业 小结 ‎1．相似三角形对应角相等，对应边成比例．‎ ‎2．相似三角形对应中线、角平分线、高的比等于相似比，周长比等于相似比，面积比等于相似比的平方．‎ 布置作业 从教材相应练习和“习题23.3”中选取．‎ 本课时从复习已经学习过的相似三角形的性质入手，提出问题继续探究相似三角形的有关性质，通过动手测量，猜想出结论，并加以证明，加深对知识的理解，提高学生分析、归纳、表达、逻辑推理等能力，并通过对知识方法的总结，培养反思问题的习惯，形成理性思维．‎ 2‎