人教版九年级数学上册第二十四章圆直线和圆的位置关系课件
第二十四章 圆
人教版
九年级数学上册
直线和圆的位置关系
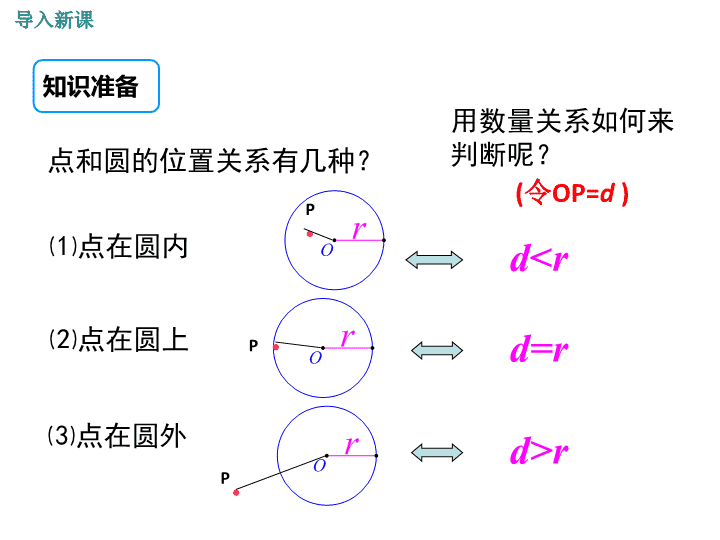
点和圆的位置关系有几种?
d
r
用数量关系如何来
判断呢?
⑴点在圆内 rO·P
⑵点在圆上 rO·P
⑶点在圆外 rO
·P
(令OP=d )
导入新课
知识准备
问题1 如果我们把太阳看成一个圆,地平线看成一
条直线,那你能根据直线和圆的公共点个数想象一
下,直线和圆有几种位置关系吗?
讲授新课
用定义判断直线与圆的位置关系一
问题2 请同学在纸上画一条直线l,把硬币的边缘
看作圆,在纸上移动硬币,你能发现直线和圆的公
共点个数的变化情况吗?公共点个数最少时有几个?
最多时有几个?
●
●
●
l
0 2
直线与圆的
位置关系
图形
公共点个数
公共点名称
直线名称
2个
交点
1个
切点
切线
0个
相离 相切 相交
位置关系 公共点个数
填一填:
直线和圆有唯一的公共点(即直线和圆相切)
时,这条直线叫做圆的切线(如图直线l),这个
唯一的公共点叫做切点(如图点A).
A l
O
要点归纳
1.直线与圆最多有两个公共点.
2.若直线与圆相交,则直线上的点都在圆上.
3.若A是⊙ O上一点,则直线AB与⊙ O相切.
4.若C为⊙ O外一点,则过点C的直线与⊙ O相交
或相离.
5.直线a 和⊙ O有公共点,则直线a与⊙ O相交.
判一判:
√
×
×
×
×
问题1 同学们用直尺在圆上移动的过程中,除了发
现公共点的个数发生了变化外,还发现有什么量也
在改变?它与圆的半径有什么样的数量关系呢?
相关知识:
点到直线的距离是指从直线外一点(A)到直线
(l)的垂线段(OA)的长度.
l
A
O
用数量关系判断直线与圆的位置关系二
问题2 怎样用d(圆心与直线的距离)来判别直线与圆
的位置关系呢?
O
d
合作探究
直线和圆相交 d< r
直线和圆相切 d= r
直线和圆相离 d> r
rd
∟
rd
∟
r
d
数形结合:位置关系 数量关系
(用圆心O到直线的距离d与圆的半径r的关系来区分)
o o o
公共点
个数
要点归纳
1.已知圆的半径为6cm,设直线和圆心的距离为d :
(3)若d=8cm ,则直线与圆______, 直线与圆有____个公共点.
(2)若d=6cm ,则直线与圆______, 直线与圆有____个公共点.
(1)若d=4cm ,则直线与圆 , 直线与圆有____个公共点.
(3)若AB和⊙ O相交,则 .
2.已知⊙ O的半径为5cm, 圆心O与直线AB的距离为d, 根据条件
填写d的范围:
(1)若AB和⊙ O相离, 则 ;
(2)若AB和⊙ O相切, 则 ;
相交
相切
相离
d > 5cm
d = 5cm
0cm≤d < 5cm
2
1
0
练一练:
B
C A
4
3
例1 在Rt△ABC中,∠C=90°,AC=3cm,BC=4cm,
以C为圆心,r为半径的圆与AB有怎样的位置关系?
为什么?
(1) r=2cm;(2) r=2.4cm; (3) r=3cm.
分析:要了解AB与⊙ C的位置关系,只要知
道圆心C到AB的距离d与r的关系.已知r,只
需求出C到AB的距离d. D
典例精析
解:过C作CD⊥AB,垂足为D.
在△ABC中,
AB= 2 2AC BC 2 23 4 5.
根据三角形的面积公式有
1 1 .2 2CD AB AC BC
∴ 3 4 2.4(cm),5
AC BCCD AB
即圆心C到AB的距离d=2.4cm.
所以 (1)当r=2cm时, 有d >r,
因此⊙ C和AB相离.
B
C A
4
3
Dd
记住:斜边上的
高等于两直角边
的乘积除以斜边.
(2)当r=2.4cm时,有d=r.
因此⊙ C和AB相切.
B
C A
4
3
D
d
(3)当r=3cm时,有d 5 C. r = 5 D. r ≥ 5
3. ☉O的最大弦长为8,若圆心O到直线l的距离为d=5,
则直线l与☉O .
4. ☉O的半径为5,直线l上的一点到圆心O的距离是5,
则直线l与☉O的位置关系是( )
A. 相交或相切 B. 相交或相离
C. 相切或相离 D. 上三种情况都有可能
B
相离
A
解析:过点A作AQ⊥MN于Q,连接AN,设半径为r,由垂
径定理有MQ=NQ,所以AQ=2,AN=r,NQ=4-r,利用
勾股定理可以求出NQ=1.5,所以N点坐标为(-1,-2).故
选A.
5.如图,在平面直角坐标系中,⊙ A与y轴相切于原点
O,平行于x轴的直线交⊙ A于M、N两点.若点M的坐
标是(-4,-2),则点N的坐标为( )
A.(-1,-2) B.(1,2)
C.(-1.5,-2) D.(1.5,-2)
A