数学华东师大版九年级上册教案22-3 实践与探索 第1课时

数学华东师大版九年级上册教案22-3 实践与探索 第1课时

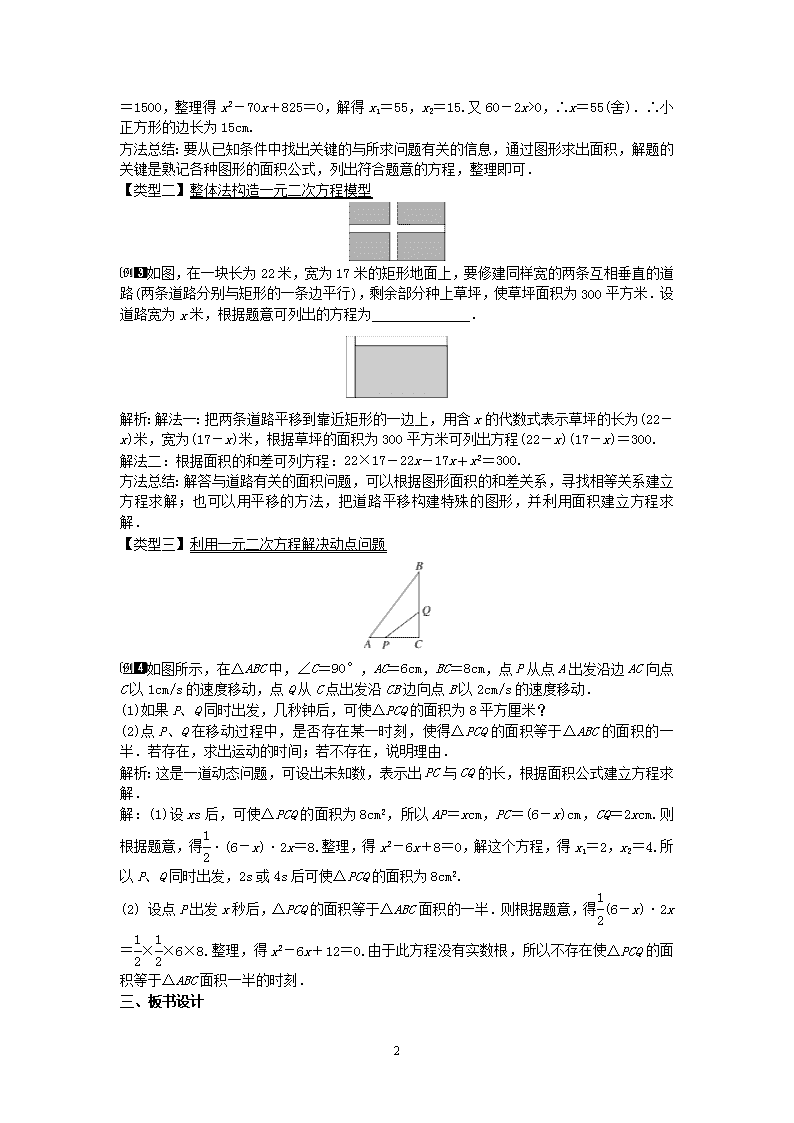
1 22.3 实践与探索 第 1 课时 教学目标 1．掌握面积法建立一元二次方程的数学模型并运用它解决实际问题． 2．继续探究实际问题中的数量关系，列出一元二次方程解应用题． 3．通过探究体会列方程的实质，提高灵活处理问题的能力． 教学重难点 【教学重点】 列出一元二次方程解应用题. 【教学难点】 用面积法建立一元二次方程的数学模型并运用它解决实际问题. 课前准备 无 教学过程 一、情境导入 如图，在长为 10cm，宽为 8cm 的矩形的四个角上截去四个全等的小正方形，使得留下的图 形(图中阴影部分)面积是原矩形面积的 80%，你能求出所截去小正方形的边长吗？ 二、合作探究 探究点：用一元二次方程解决图形面积问题 【类型一】利用面积构造一元二次方程模型 用 10 米长的铝材制成一个矩形窗框，使它的面积为 6 平方米．若设它的一条边长为 x 米，则根据题意可列出关于 x 的方程为( ) A．x(5＋x)＝6 B．x(5－x)＝6 C．x(10－x)＝6 D．x(10－2x)＝6 解析：设一边长为 x 米，则另外一边长为(5－x)米，根据它的面积为 6 平方米，即可列出方 程得：x(5－x)＝6，故选择 B. 方法总结：理解题意，恰当的设未知数，把题中相关的量用未知数表示出来，用相等关系列 出方程． 现有一块长 80cm、宽 60cm 的矩形钢片，将它的四个角各剪去一个边长为 xcm 的小正 方形，做成一个底面积为 1500cm2 的无盖的长方体盒子，求小正方形的边长． 解析：设小正方形的边长为 xcm，则长方体盒子底面的长、宽均可用含 x 的代数式表示，再 根据面积，即可建立等量关系，列出方程． 解：设小正方形的边长为 xcm，则可得这个长方体盒子的底面的长是(80－2x)cm，宽是(60 －2x)cm，根据矩形的面积的计算方法即可表示出矩形的底面积，方程可列为(80－2x)(60 2 －2x)＝1500，整理得 x2－70x＋825＝0，解得 x1＝55，x2＝15.又 60－2x>0，∴x＝55(舍)．∴ 小正方形的边长为 15cm. 方法总结：要从已知条件中找出关键的与所求问题有关的信息，通过图形求出面积，解题的 关键是熟记各种图形的面积公式，列出符合题意的方程，整理即可． 【类型二】整体法构造一元二次方程模型 如图，在一块长为 22 米，宽为 17 米的矩形地面上，要修建同样宽的两条互相垂直的道 路(两条道路分别与矩形的一条边平行)，剩余部分种上草坪，使草坪面积为 300 平方米．设 道路宽为 x 米，根据题意可列出的方程为______________． 解析：解法一：把两条道路平移到靠近矩形的一边上，用含 x 的代数式表示草坪的长为(22 －x)米，宽为(17－x)米，根据草坪的面积为 300 平方米可列出方程(22－x)(17－x)＝300. 解法二：根据面积的和差可列方程：22×17－22x－17x＋x2＝300. 方法总结：解答与道路有关的面积问题，可以根据图形面积的和差关系，寻找相等关系建立 方程求解；也可以用平移的方法，把道路平移构建特殊的图形，并利用面积建立方程求解． 【类型三】利用一元二次方程解决动点问题 如图所示，在△ABC 中，∠C＝90°，AC＝6cm，BC＝8cm，点 P 从点 A 出发沿边 AC 向 点 C 以 1cm/s 的速度移动，点 Q 从 C 点出发沿 CB 边向点 B 以 2cm/s 的速度移动． (1)如果 P、Q 同时出发，几秒钟后，可使△PCQ 的面积为 8 平方厘米？ (2)点 P、Q 在移动过程中，是否存在某一时刻，使得△PCQ 的面积等于△ABC 的面积的一半．若 存在，求出运动的时间；若不存在，说明理由． 解析：这是一道动态问题，可设出未知数，表示出 PC 与 CQ 的长，根据面积公式建立方程求 解． 解：(1)设 xs 后，可使△PCQ 的面积为 8cm2，所以 AP＝xcm，PC＝(6－x)cm，CQ＝2xcm.则根 据题意，得1 2 ·(6－x)·2x＝8.整理，得 x2－6x＋8＝0，解这个方程，得 x1＝2，x2＝4.所以 P、Q 同时出发，2s 或 4s 后可使△PCQ 的面积为 8cm2. (2) 设点 P 出发 x 秒后，△PCQ 的面积等于△ABC 面积的一半．则根据题意，得1 2 (6－x)·2x ＝1 2 ×1 2 ×6×8.整理，得 x2－6x＋12＝0.由于此方程没有实数根，所以不存在使△PCQ 的面 积等于△ABC 面积一半的时刻． 三、板书设计 3 四、教学反思 与图形有关的问题是一元二次方程应用的常见题型，解决这类问题的关键是将不规则图形分 割或补全成规则图形，找出各部分面积之间的关系，运用面积等计算公式列出方程；对图形 进行分割或补全的原则：转化成为规则图形时越简单越直观越好.