2020年广东省中山市 梅州市 汕尾市 汕头市 惠州市 中考数学试卷【含答案；可编辑】

2020年广东省中山市 梅州市 汕尾市 汕头市 惠州市 中考数学试卷【含答案；可编辑】

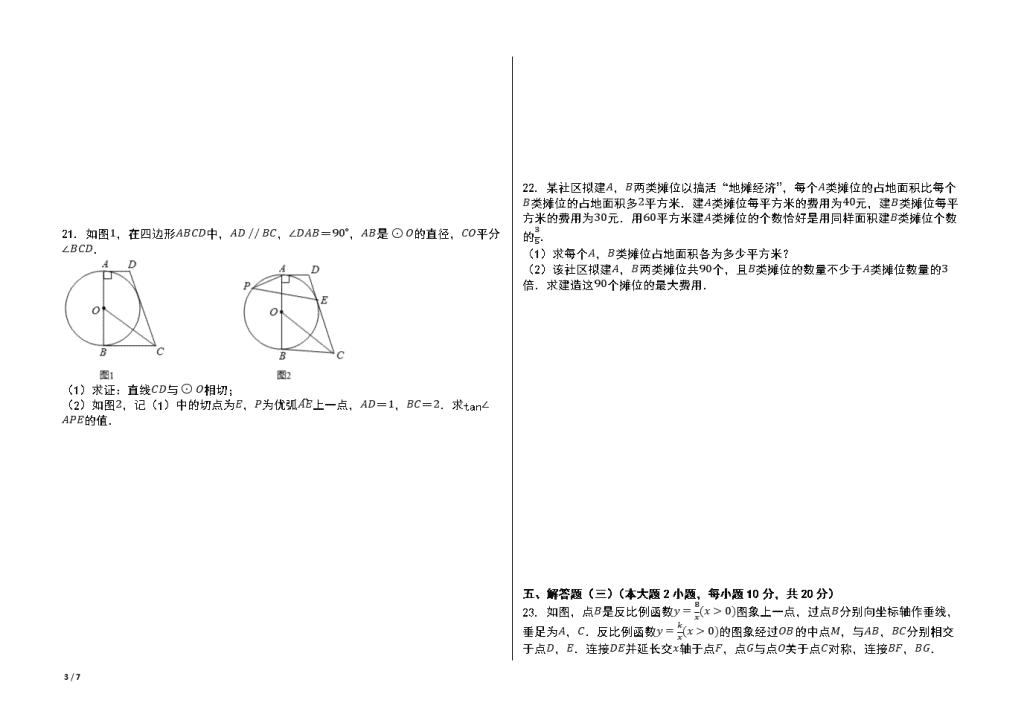
‎2020年广东省中山市 梅州市 汕尾市 汕头市 惠州市 中考数学试卷【含答案；可编辑】‎ 一、选择题（本大题10小题，每小题3分，共30分）在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑．‎ ‎1. ‎9‎的相反数是（ ）‎ A.‎-9‎ B.‎9‎ C.‎1‎‎9‎ D.‎‎-‎‎1‎‎9‎ ‎2. 一组数据‎2‎，‎4‎，‎3‎，‎5‎，‎2‎的中位数是（ ）‎ A.‎5‎ B.‎3.5‎ C.‎3‎ D.‎‎2.5‎ ‎3. 在平面直角坐标系中，点‎(3, 2)‎关于x轴对称的点的坐标为（ ）‎ A.‎(-3, 2)‎ B.‎(-2, 3)‎ C.‎(2, -3)‎ D.‎‎(3, -2)‎ ‎4. 若一个多边形的内角和是‎540‎‎∘‎，则该多边形的边数为（ ）‎ A.‎4‎ B.‎5‎ C.‎6‎ D.‎‎7‎ ‎5. 若式子‎2x-4‎在实数范围内有意义，则x的取值范围是（ ）‎ A.x≠2‎ B.x≥2‎ C.x≤2‎ D.‎x≠-2‎ ‎6. 已知‎△ABC的周长为‎16‎，点D，E，F分别为‎△ABC三条边的中点，则‎△DEF的周长为（ ）‎ A.‎8‎ B.‎2‎‎2‎ C.‎16‎ D.‎‎4‎ ‎7. 把函数y＝‎(x-1‎)‎‎2‎+2‎图象向右平移‎1‎个单位长度，平移后图象的函数解析式为（ ）‎ A.y＝x‎2‎‎+2‎ B.y＝‎(x-1‎)‎‎2‎+1‎ C.y＝‎(x-2‎)‎‎2‎+2‎ D.y＝‎‎(x-1‎)‎‎2‎+3‎ ‎8. 不等式组‎2-3x≥-1,‎x-1≥-2(x+2)‎‎ ‎的解集为（ ）‎ A.无解 B.x≤1‎ C.x≥-1‎ D.‎‎-1≤x≤1‎ ‎9. 如图，在正方形ABCD中，AB＝‎3‎，点E，F分别在边AB，CD上，‎∠EFD＝‎60‎‎∘‎．若将四边形EBCF沿EF折叠，点B恰好落在AD边上，则BE的长度为（ ）‎ A.‎1‎ B.‎2‎ C.‎3‎ D.‎‎2‎ ‎10. 如图，抛物线y＝ax‎2‎+bx+c的对称轴是x＝‎1‎，下列结论：‎ ‎①abc>0‎；②b‎2‎‎-4ac>0‎；③‎8a+c<0‎；④‎5a+b+2c>0‎，‎ 正确的有（ ）‎ A.‎4‎个 B.‎3‎个 C.‎2‎个 D.‎1‎个 二、填空题（本大题7小题，每小题4分，共28分）请将下列各题的正确答案填写在答题卡相应的位置上．‎ ‎11. 分解因式：xy-x＝________．‎ ‎12. 如果单项式‎3xmy与‎-5‎x‎3‎yn是同类项，那么m+n＝________．‎ ‎13. 若a-2‎‎+|b+1|‎＝‎0‎，则‎(a+b‎)‎‎2020‎＝________．‎ ‎14. 已知x＝‎5-y，xy＝‎2‎，计算‎3x+3y-4xy的值为________．‎ ‎15. 如图，在菱形ABCD中，‎∠A＝‎30‎‎∘‎，取大于‎1‎‎2‎AB的长为半径，分别以点A，B为圆心作弧相交于两点，过此两点的直线交AD边于点E（作图痕迹如图所示），连接BE，BD．则‎∠EBD的度数为________．‎ ‎16. 有一架竖直靠在直角墙面的梯子正在下滑，一只猫紧紧盯住位于梯子正中间的老鼠，等待与老鼠距离最小时扑捉．把墙面、梯子、猫和老鼠都理想化为同一平面内的线或点，模型如图，‎∠ABC＝‎90‎‎∘‎，点M，N分别在射线BA，BC上，MN长度始终保持不变，MN＝‎4‎，E为MN的中点，点D到BA，BC的距离分别为‎4‎和‎2‎．在此滑动过程中，猫与老鼠的距离DE的最小值为________．‎ 三、解答题（一）（本大题3小题，每小题6分，共18分）‎ ‎17. 先化简，再求值：‎(x+y‎)‎‎2‎+(x+y)(x-y)-2‎x‎2‎，其中x=‎‎2‎，y=‎‎3‎．‎ ‎ 7 / 7‎ ‎18. 某中学开展主题为“垃圾分类知多少”的调查活动，调查问卷设置了“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级，要求每名学生选且只能选其中一个等级，随机抽取了‎120‎名学生的有效问卷，数据整理如下：‎ 等级 非常了解 比较了解 基本了解 不太了解 人数（人）‎ ‎24‎ ‎72‎ ‎18‎ x ‎（1）求x的值；‎ ‎（2）若该校有学生‎1800‎人，请根据抽样调查结果估算该校“非常了解”和“比较了解”垃圾分类知识的学生共有多少人？‎ ‎19. 如图，在‎△ABC中，点D，E分别是AB、AC边上的点，BD＝CE，‎∠ABE＝‎∠ACD，BE与CD相交于点F．求证：‎△ABC是等腰三角形．‎ 四、解答题（二）（本大题3小题，每小题8分，共24分）‎ ‎20. 已知关于x，y的方程组ax+2‎3‎y=-10‎3‎,‎x+y=4‎‎ ‎与x-y=2,‎x+by=15‎‎ ‎的解相同．‎ ‎（1）求a，b的值；‎ ‎（2）若一个三角形的一条边的长为‎2‎‎6‎，另外两条边的长是关于x的方程x‎2‎‎+ax+b＝‎0‎的解．试判断该三角形的形状，并说明理由．‎ ‎ 7 / 7‎ ‎21. 如图‎1‎，在四边形ABCD中，AD // BC，‎∠DAB＝‎90‎‎∘‎，AB是‎⊙O的直径，CO平分‎∠BCD．‎ ‎（1）求证：直线CD与‎⊙O相切；‎ ‎（2）如图‎2‎，记（1）中的切点为E，P为优弧AE上一点，AD＝‎1‎，BC＝‎2‎．求tan∠APE的值．‎ ‎22. 某社区拟建A，B两类摊位以搞活“地摊经济”，每个A类摊位的占地面积比每个B类摊位的占地面积多‎2‎平方米．建A类摊位每平方米的费用为‎40‎元，建B类摊位每平方米的费用为‎30‎元．用‎60‎平方米建A类摊位的个数恰好是用同样面积建B类摊位个数的‎3‎‎5‎．‎ ‎（1）求每个A，B类摊位占地面积各为多少平方米？‎ ‎（2）该社区拟建A，B两类摊位共‎90‎个，且B类摊位的数量不少于A类摊位数量的‎3‎倍．求建造这‎90‎个摊位的最大费用．‎ 五、解答题（三）（本大题2小题，每小题10分，共20分）‎ ‎23. 如图，点B是反比例函数y=‎8‎x(x>0)‎图象上一点，过点B分别向坐标轴作垂线，垂足为A，C．反比例函数y=kx(x>0)‎的图象经过OB的中点M，与AB，BC分别相交于点D，E．连接DE并延长交x轴于点F，点G与点O关于点C对称，连接BF，BG．‎ ‎ 7 / 7‎ ‎（1）填空：k＝________；‎ ‎（2）求‎△BDF的面积；‎ ‎（3）求证：四边形BDFG为平行四边形．‎ ‎24. 如图，抛物线y=‎3+‎‎3‎‎6‎x‎2‎+bx+c与x轴交于A，B两点，点A，B分别位于原点的左、右两侧，BO＝‎3AO＝‎3‎，过点B的直线与y轴正半轴和抛物线的交点分别为C，D，BC=‎3‎CD．‎ ‎（1）求b，c的值；‎ ‎（2）求直线BD的函数解析式；‎ ‎（3）点P在抛物线的对称轴上且在x轴下方，点Q在射线BA上．当‎△ABD与‎△BPQ相似时，请直接写出所有满足条件的点Q的坐标．‎ ‎ 7 / 7‎ 参考答案与试题解析 ‎2020年广东省中山市 梅州市 汕尾市 汕头市 惠州市 中考数学试卷【含答案；可编辑】‎ 一、选择题（本大题10小题，每小题3分，共30分）在每小题列出的四个选项中，只有一个是正确的，请把答题卡上对应题目所选的选项涂黑．‎ ‎1.A ‎2.C ‎3.D ‎4.B ‎5.B ‎6.A ‎7.C ‎8.D ‎9.D ‎10.B 二、填空题（本大题7小题，每小题4分，共28分）请将下列各题的正确答案填写在答题卡相应的位置上．‎ ‎11.‎x(y-1)‎ ‎12.‎‎4‎ ‎13.‎‎1‎ ‎14.‎‎7‎ ‎15.‎‎45‎‎∘‎ ‎16.‎‎2‎5‎-2‎ 三、解答题（一）（本大题3小题，每小题6分，共18分）‎ ‎17.‎(x+y‎)‎‎2‎+(x+y)(x-y)-2‎x‎2‎，‎ ‎＝‎x‎2‎‎+2xy+y‎2‎+x‎2‎-y‎2‎-2‎x‎2‎ ‎＝‎2xy，‎ 当x=‎‎2‎，y=‎‎3‎时，‎ 原式＝‎2×‎2‎×‎3‎=2‎‎6‎．‎ ‎18.x＝‎120-(24+72+18)‎＝‎6‎；‎ ‎1800×‎24+72‎‎120‎=1440‎‎（人），‎ 答：根据抽样调查结果估算该校“非常了解”和“比较了解”垃圾分类知识的学生共有‎1440‎人．‎ ‎19.证明：∵ ‎∠ABE＝‎∠ACD，‎ ‎∴ ‎∠DBF＝‎∠ECF，‎ 在‎△BDF和‎△CEF中，‎∠DBF=∠ECF‎∠BFD=∠CFEBD=CE‎ ‎，‎ ‎∴ ‎△BDF≅△CEF(AAS)‎，‎ ‎∴ BF＝CF，DF＝EF，‎ ‎∴ ‎∠FBC＝‎∠FCB，‎ ‎∴ ‎∠ABC＝‎∠ACB，‎ ‎∴ AB＝AC，‎ 即‎△ABC是等腰三角形．‎ 四、解答题（二）（本大题3小题，每小题8分，共24分）‎ ‎20.由题意得，关于x，y的方程组的相同解，就是方程组x+y=4‎x-y=2‎‎ ‎的解，‎ 解得，x=3‎y=1‎‎ ‎，代入原方程组得，a＝‎-4‎‎3‎，b＝‎12‎；‎ 当a＝‎-4‎‎3‎，b＝‎12‎时，关于x的方程x‎2‎‎+ax+b＝‎0‎就变为x‎2-‎‎4‎3‎x+12‎＝‎0‎，‎ 解得，x‎1‎＝x‎2‎＝‎2‎‎3‎，‎ 又∵ ‎(2‎3‎‎)‎‎2‎+(2‎‎3‎‎)‎‎2‎＝‎(2‎‎6‎‎)‎‎2‎，‎ ‎∴ 以‎2‎‎3‎、‎2‎‎3‎、‎2‎‎6‎为边的三角形是等腰直角三角形．‎ ‎21.证明：作OE⊥CD于E，如图‎1‎所示：‎ 则‎∠OEC＝‎90‎‎∘‎，‎ ‎∵ AD // BC，‎∠DAB＝‎90‎‎∘‎，‎ ‎∴ ‎∠OBC＝‎180‎‎∘‎‎-∠DAB＝‎90‎‎∘‎，‎ ‎∴ ‎∠OEC＝‎∠OBC，‎ ‎∵ CO平分‎∠BCD，‎ ‎∴ ‎∠OCE＝‎∠OCB，‎ 在‎△OCE和‎△OCB中，‎∠OEC=∠OBC‎∠OCE=∠OCBOC=OC‎ ‎，‎ ‎∴ ‎△OCE≅△OCB(AAS)‎，‎ ‎∴ OE＝OB，‎ 又∵ OE⊥CD，‎ ‎∴ 直线CD与‎⊙O相切；‎ 作DF⊥BC于F，连接BE，如图‎2‎所示：‎ 则四边形ABFD是矩形，‎ ‎∴ AB＝DF，BF＝AD＝‎1‎，‎ ‎∴ CF＝BC-BF＝‎2-1‎＝‎1‎，‎ ‎∵ AD // BC，‎∠DAB＝‎90‎‎∘‎，‎ ‎∴ AD⊥AB，BC⊥AB，‎ ‎∴ AD、BC是‎⊙O的切线，‎ 由（1）得：CD是‎⊙O的切线，‎ ‎∴ ED＝AD＝‎1‎，EC＝BC＝‎2‎，‎ ‎∴ CD＝ED+EC＝‎3‎，‎ ‎∴ DF=CD‎2‎-CF‎2‎=‎3‎‎2‎‎-‎‎1‎‎2‎=2‎‎2‎，‎ ‎∴ AB＝DF＝‎2‎‎2‎，‎ ‎ 7 / 7‎ ‎∴ OB=‎‎2‎，‎ ‎∵ CO平分‎∠BCD，‎ ‎∴ CO⊥BE，‎ ‎∴ ‎∠BCH+∠CBH＝‎∠CBH+∠ABE＝‎90‎‎∘‎，‎ ‎∴ ‎∠ABE＝‎∠BCH，‎ ‎∵ ‎∠APE＝‎∠ABE，‎ ‎∴ ‎∠APE＝‎∠BCH，‎ ‎∴ tan∠APE＝tan∠BCH=OBBC=‎‎2‎‎2‎．‎ ‎22.每个A类摊位占地面积为‎5‎平方米，每个B类摊位的占地面积为‎3‎平方米；‎ 建造这‎90‎个摊位的最大费用是‎10520‎元 五、解答题（三）（本大题2小题，每小题10分，共20分）‎ ‎23.‎‎2‎ ‎△BDF的面积＝‎△OBD的面积＝S‎△BOA‎-S‎△OAD=‎1‎‎2‎×8-‎1‎‎2‎×2‎＝‎3‎；‎ 设点D(m, ‎2‎m)‎，则点B(4m, ‎2‎m)‎，‎ ‎∵ 点G与点O关于点C对称，故点G(8m, 0)‎，‎ 则点E(4m, ‎1‎‎2m)‎，‎ 设直线DE的表达式为：y＝sx+n，将点D、E的坐标代入上式得‎2‎m‎=ms+n‎1‎‎2m‎=4ms+n‎ ‎并解得：‎ 直线DE的表达式为：y=-‎1‎‎2‎m‎2‎x+‎‎5‎‎2m，令y＝‎0‎，则x＝‎5m，故点F(5m, 0)‎，‎ 故FG＝‎8m-5m＝‎3m，而BD＝‎4m-m＝‎3m＝FG，‎ 则FG // BD，故四边形BDFG为平行四边形．‎ ‎24.∵ BO＝‎3AO＝‎3‎，‎ ‎∴ 点B(3, 0)‎，点A(-1, 0)‎，‎ ‎∴ 抛物线解析式为：y=‎3+‎‎3‎‎6‎(x+1)(x-3)=‎3+‎‎3‎‎6‎x‎2‎-‎3+‎‎3‎‎3‎x-‎‎3+‎‎3‎‎2‎，‎ ‎∴ b=-‎‎3+‎‎3‎‎3‎，c=-‎‎3+‎‎3‎‎2‎；‎ 如图‎1‎，过点D作DE⊥AB于E，‎ ‎∴ CO // DE，‎ ‎∴ BCCD‎=‎BOOE，‎ ‎∵ BC=‎3‎CD，BO＝‎3‎，‎ ‎∴ ‎3‎‎=‎‎3‎OE，‎ ‎∴ OE=‎‎3‎，‎ ‎∴ 点D横坐标为‎-‎‎3‎，‎ ‎∴ 点D坐标为‎(-‎3‎, ‎3‎+1)‎，‎ 设直线BD的函数解析式为：y＝kx+b，‎ 由题意可得：‎3‎‎+1=-‎3‎k+b‎0=3k+b‎ ‎，‎ 解得：k=-‎‎3‎‎3‎b=‎‎3‎‎ ‎，‎ ‎∴ 直线BD的函数解析式为y=-‎3‎‎3‎x+‎‎3‎；‎ ‎∵ 点B(3, 0)‎，点A(-1, 0)‎，点D(-‎3‎, ‎3‎+1)‎，‎ ‎∴ AB＝‎4‎，AD＝‎2‎‎2‎，BD＝‎2‎3‎+2‎，对称轴为直线x＝‎1‎，‎ ‎∵ 直线BD:y=-‎3‎‎3‎x+‎‎3‎与y轴交于点C，‎ ‎∴ 点C(0, ‎3‎)‎，‎ ‎∴ OC=‎‎3‎，‎ ‎∵ tan∠CBO=COBO=‎‎3‎‎3‎，‎ ‎ 7 / 7‎ ‎∴ ‎∠CBO＝‎30‎‎∘‎，‎ 如图‎2‎，过点A作AK⊥BD于K，‎ ‎∴ AK=‎1‎‎2‎AB＝‎2‎，‎ ‎∴ DK=AD‎​‎‎2‎-AK‎​‎‎2‎=‎8-4‎=2‎，‎ ‎∴ DK＝AK，‎ ‎∴ ‎∠ADB＝‎45‎‎∘‎，‎ 如图，设对称轴与x轴的交点为N，即点N(1, 0)‎，‎ 若‎∠CBO＝‎∠PBO＝‎30‎‎∘‎，‎ ‎∴ BN=‎3‎PN＝‎2‎，BP＝‎2PN，‎ ‎∴ PN=‎‎2‎‎3‎‎3‎，BP=‎‎4‎‎3‎‎3‎，‎ 当‎△BAD∽△BPQ，‎ ‎∴ BPBA‎=‎BQBD，‎ ‎∴ BQ=‎4‎‎3‎‎3‎‎×(2‎3‎+2)‎‎4‎=2+‎‎2‎‎3‎‎3‎，‎ ‎∴ 点Q(1-‎2‎‎3‎‎3‎, 0)‎；‎ 当‎△BAD∽△BQP，‎ ‎∴ BPBD‎=‎BQAB，‎ ‎∴ BQ=‎4‎‎3‎‎3‎‎×4‎‎2‎3‎+2‎=4-‎‎4‎‎3‎‎3‎，‎ ‎∴ 点Q(-1+‎4‎‎3‎‎3‎, 0)‎；‎ 若‎∠PBO＝‎∠ADB＝‎45‎‎∘‎，‎ ‎∴ BN＝PN＝‎2‎，BP=‎2‎BN＝‎2‎‎2‎，‎ 当‎△DAB∽△BPQ，‎ ‎∴ BPAD‎=‎BQBD，‎ ‎∴ ‎2‎‎2‎‎2‎‎2‎‎=‎BQ‎2‎3‎+2‎，‎ ‎∴ BQ＝‎‎2‎3‎+2‎ ‎∴ 点Q(1-2‎3‎, 0)‎；‎ 当‎△BAD∽△PQB，‎ ‎∴ BPBD‎=‎BQAD，‎ ‎∴ BQ=‎2‎2‎×2‎‎2‎‎2‎3‎+2‎=2‎3‎-2‎，‎ ‎∴ 点Q(5-2‎3‎, 0)‎；‎ 综上所述：满足条件的点Q的坐标为‎(1-‎2‎‎3‎‎3‎, 0)‎或‎(-1+‎4‎‎3‎‎3‎, 0)‎或‎(1-2‎3‎, 0)‎或‎(5-2‎3‎, 0)‎．‎ ‎ 7 / 7‎