2020年上海市金山区中考数学二模试卷
2020年上海市金山区中考数学二模试卷
一、选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,请选择正确选项的代号并填涂在答题纸的相应位置上】
1. 在下列各数中,无理数是( )
A.207 B.π3 C.4 D.0.101001
2. 计算(a3)2的结果是( )
A.a B.a5 C.a6 D.a9
3. 一次函数y=2x−3的图象在y轴的截距是( )
A.2 B.−2 C.3 D.−3
4. 某区对创建全国文明城区的满意程度进行随机调查,结果如图所示,据此可估计全区75万居民对创建全国文明城区工作不满意的居民人数为( )
A.1.2万 B.1.5万 C.7.5万 D.66万
5. 已知在△ABC中,AD是中线,设AB→=m→,AD→=n→,那么向量BC→用向量m→,n→表示为( )
A.2m→−2n→ B.2m→+2n→ C.2n→−2m→ D.n→−m→
6. 如图,∠MON=30∘,OP是∠MON的角平分线,PQ // ON交OM于点Q,以P为圆心半径为4的圆与ON相切,如果以Q为圆心半径为r的圆与⊙P相交,那么r的取值范围是( )
A.4
4
二、填空题:(本大题共12题,每题4分,满分48分)
分解因式:a2−4=________.
某种冠状病毒的直径大约是0.00011毫米,数据0.00011用科学记数法表示为________.
方程2−x=x的根是________.
已知关于x的方程x2−mx+2=0有两个相等的实数根,那么m的值是________.
函数y=13−x的定义域是________.
从 1,2,3,4,5,6,7,8,9,10这十个数中随机取出一个数,取出的数是3的倍数的概率是________.
某学校九年级共有350名学生,在一次九年级全体学生参加的数学测试中,随机抽取50名学生的测试成绩进行抽样调查,绘制频率分布直方图如图所示,如果成绩不低于80分算优良,那么估计九年级全体学生在这次测试中成绩优良学生人数约是________.
上海市居民用户燃气收费标准如表:
年用气量(立方米)
每立方米价格(元)
第一档0−−−310
3.00
第二档310(含)−−−520(含)
3.30
第三档520以上
4.20
某居民用户用气量在第一档,那么该用户每年燃气费y(元)与年用气量x(立方米)的函数关系式是________.
第25页 共26页 ◎ 第26页 共26页
四边形ABCD中,对角线AC、BD相互垂直,AC=4,BD=6,顺次联结这个四边形中点所得的四边形的面积等于________.
我们把正多边形的一个内角与外角的比值叫做正多边形的内外比,内外比为3的正多边形的边数为________.
如图,在坡度为1:2.4的斜坡上有一棵与水平面垂直的树BC,在斜坡底部A处测得树顶C的仰角为30∘,AB的长为65米,那么树高BC等于________米(保留根号).
如图,在△ABC中,∠C=90∘,AC=3,BC=4,把△ABC绕C点旋转得到△A′B′C,其中点A′在线段AB上,那么∠A′B′B的正切值等于________.
三、解答题:(本大题共7题,满分78分)
计算:12+(3−1)−1−(18)13+cos30∘.
解方程组:x−y=2x2−xy−y2=1 .
在平面直角坐标系xOy中(如图),已知函数y=2x的图象和反比例函数的图象在第一象限交于A点,其中点A的横坐标是1.
(1)求反比例函数的解析式;
(2)把直线y=2x平移后与y轴相交于点B,且AB=OB,求平移后直线的解析式.
如图,已知在四边形ABCD中∠A=∠ABC=90∘,点E是CD的中点,△ABD与△EBD关于直线BD对称,AD=1,AB=3.
(1)求点A和点E之间的距离;
(2)联结AC交BE于点F,求AFAC的值.
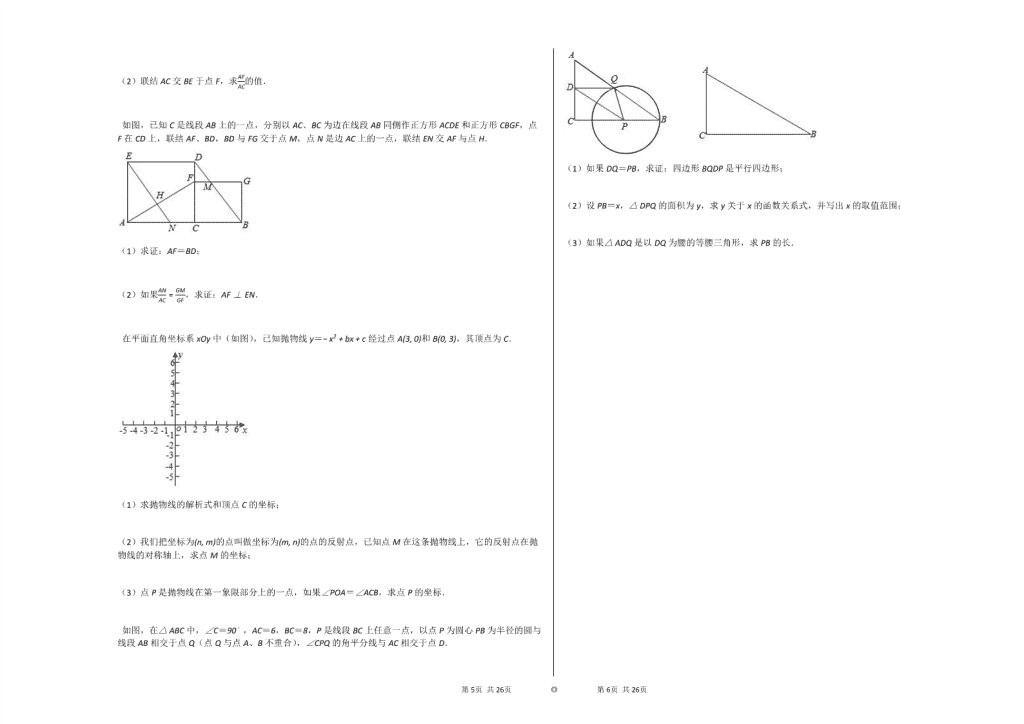
如图,已知C是线段AB上的一点,分别以AC、BC为边在线段AB同侧作正方形ACDE和正方形CBGF,点F在CD上,联结AF、BD,BD与FG交于点M,点N是边AC上的一点,联结EN交AF与点H.
(1)求证:AF=BD;
(2)如果ANAC=GMGF,求证:AF⊥EN.
第25页 共26页 ◎ 第26页 共26页
在平面直角坐标系xOy中(如图),已知抛物线y=−x2+bx+c经过点A(3, 0)和B(0, 3),其顶点为C.
(1)求抛物线的解析式和顶点C的坐标;
(2)我们把坐标为(n, m)的点叫做坐标为(m, n)的点的反射点,已知点M在这条抛物线上,它的反射点在抛物线的对称轴上,求点M的坐标;
(3)点P是抛物线在第一象限部分上的一点,如果∠POA=∠ACB,求点P的坐标.
如图,在△ABC中,∠C=90∘,AC=6,BC=8,P是线段BC上任意一点,以点P为圆心PB为半径的圆与线段AB相交于点Q(点Q与点A、B不重合),∠CPQ的角平分线与AC相交于点D.
(1)如果DQ=PB,求证:四边形BQDP是平行四边形;
(2)设PB=x,△DPQ的面积为y,求y关于x的函数关系式,并写出x的取值范围;
(3)如果△ADQ是以DQ为腰的等腰三角形,求PB的长.
第25页 共26页 ◎ 第26页 共26页
参考答案与试题解析
2020年上海市金山区中考数学二模试卷
一、选择题:(本大题共6题,每题4分,满分24分)【下列各题的四个选项中,有且只有一个选项是正确的,请选择正确选项的代号并填涂在答题纸的相应位置上】
1.
【答案】
B
【考点】
无理数的识别
算术平方根
【解析】
无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.
【解答】
A.207是分数,属于有理数;
B.π3是无理数;
C.4=2,是整数,属于有理数;
D.0.101001是有限小数,属于有理数.
2.
【答案】
C
【考点】
幂的乘方与积的乘方
【解析】
根据幂的乘方法则:底数不变,指数相乘.(am)n=amn(m,n是正整数)计算即可.
【解答】
解:(a3)2=a3×2=a6.
故选C.
3.
【答案】
D
【考点】
一次函数的图象
一次函数图象上点的坐标特点
【解析】
代入x=0,求出y值,此题得解.
【解答】
当x=0时,y=2x−3=−3,
∴ 一次函数y=2x−3的图象在y轴的截距是−3.
4.
【答案】
B
【考点】
扇形统计图
【解析】
用总人数乘以样本中对创建全国文明城区工作不满意的居民人数所对应的百分比可得.
【解答】
估计全区75万居民对创建全国文明城区工作不满意的居民人数为75×2%=1.5(万人),
5.
【答案】
C
【考点】
*平面向量
【解析】
根据向量运算法则即可求出答案.
【解答】
∵ BD→=BA→+AD→=AD→−AB→,
∴ BD→=n→−m→,
∴ BC→=2BD→=2n→−2m→,
6.
【答案】
A
【考点】
圆与圆的位置关系
切线的判定与性质
【解析】
如图,过点P作PA⊥OM于点A.根据题意首先判定OM是切线,根据切线的性质得到PA=4.由角平分线的性质和平行线的性质判定直角△APQ中含有30度角,则由“30度角所对的直角边是斜边的一半”得到PQ的长度;然后根据圆与圆的位置关系求得r的取值范围.
【解答】
如图,过点P作PA⊥OM于点A.
∵ 圆P与ON相切,设切点为B,连接PB.
∴ PB⊥ON.
∵ OP是∠MON的角平分线,
∴ PA=PB.
∴ PA是半径,
∴ OM是圆P的切线.
∵ ∠MON=30∘,OP是∠MON的角平分线,
∴ ∠1=∠2=15∘.
∵ PQ // ON,
∴ ∠3=∠2=15∘.
∴ ∠4=∠1+∠3=30∘.
∵ PA=4,
∴ PQ=2PA=8.
∴ r最小值=8−4=4,r最大值=8+4=12.
∴
第25页 共26页 ◎ 第26页 共26页
r的取值范围是4
查看更多