- 2021-11-10 发布 |
- 37.5 KB |
- 8页
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
北师大版九年级上册期末备考之考点突破:特殊平行四边形、相似、反比例函数(四)
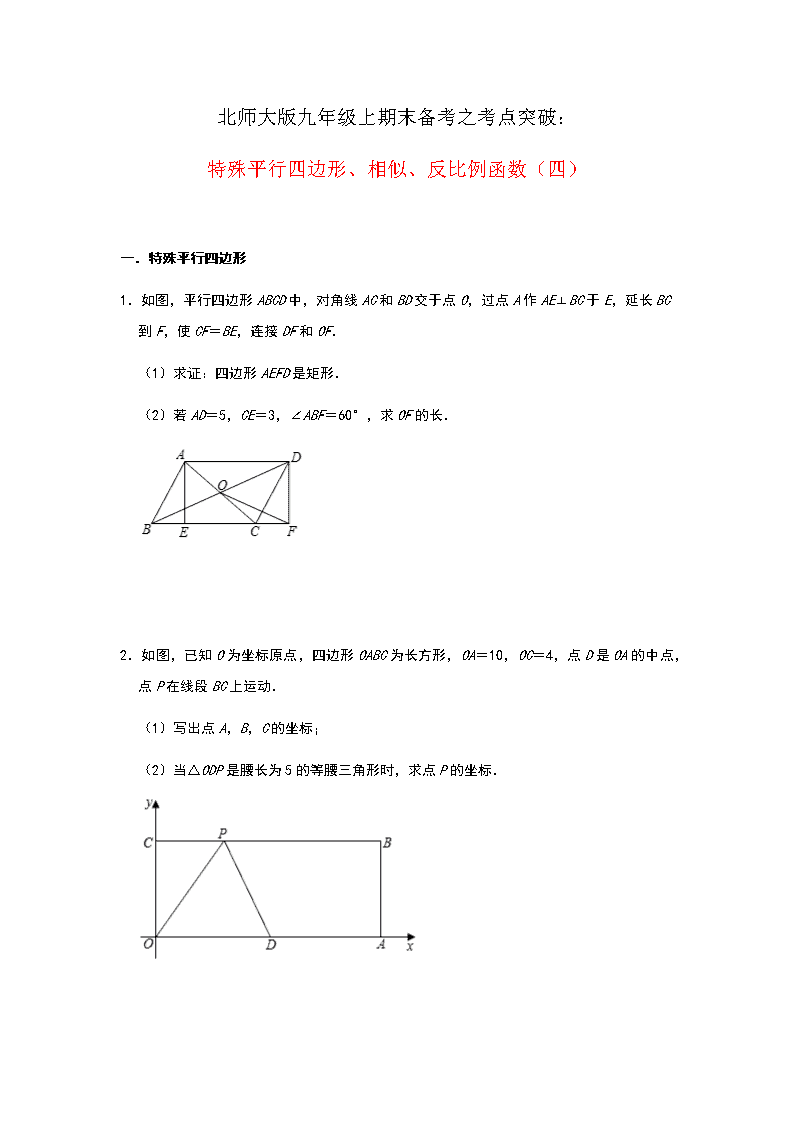
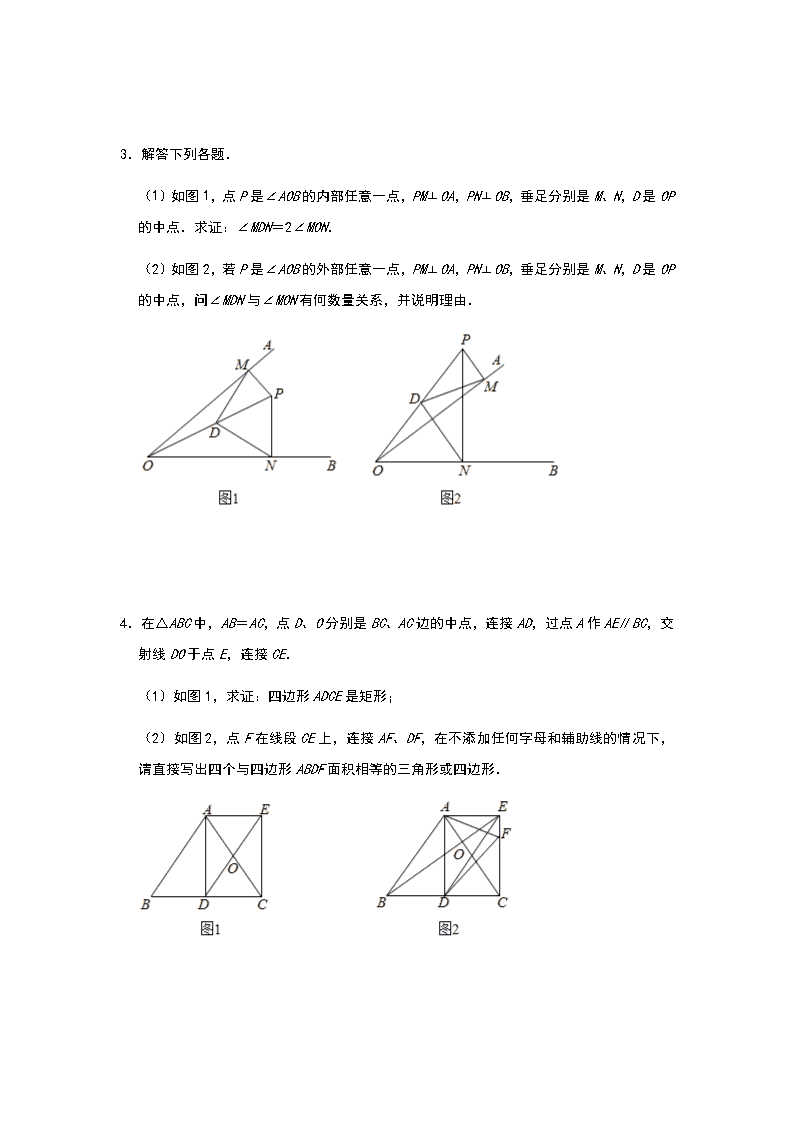
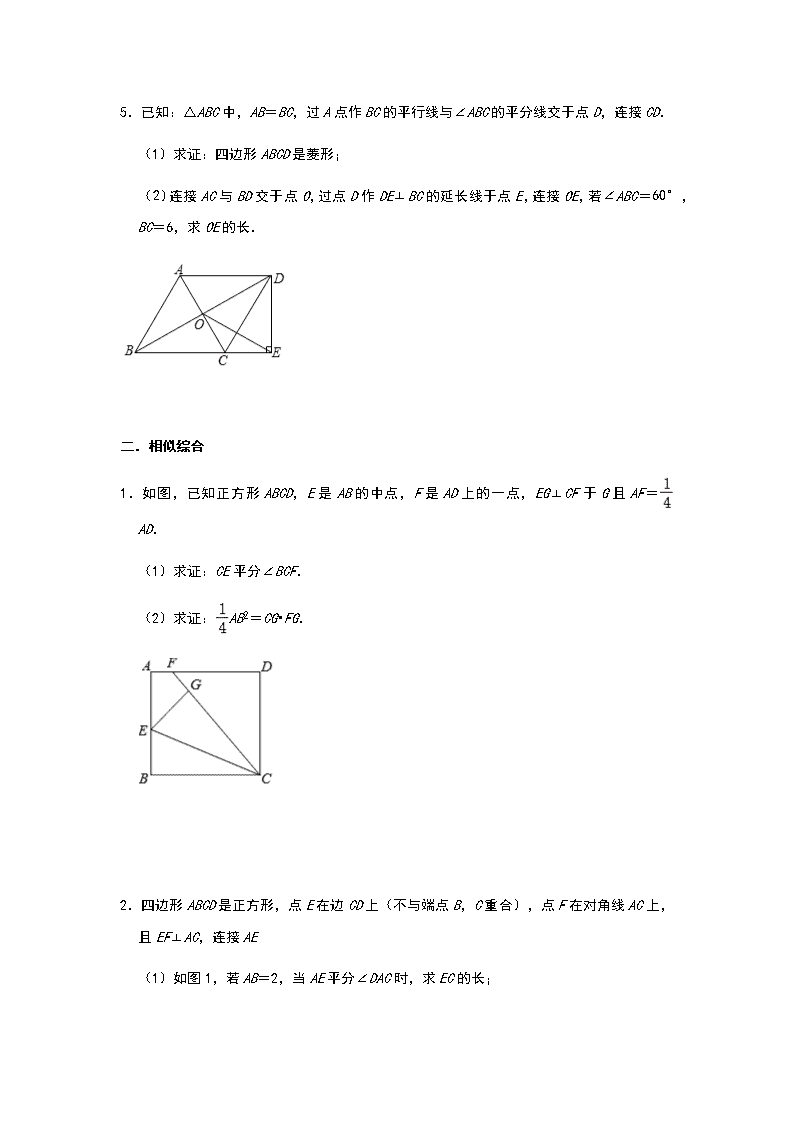
北师大版九年级上期末备考之考点突破: 特殊平行四边形、相似、反比例函数(四) 一.特殊平行四边形 1.如图,平行四边形 ABCD 中,对角线 AC 和 BD 交于点 O,过点 A 作 AE⊥BC 于 E,延长 BC 到 F,使 CF=BE,连接 DF 和 OF. (1)求证:四边形 AEFD 是矩形. (2)若 AD=5,CE=3,∠ABF=60°,求 OF 的长. 2.如图,已知 O为坐标原点,四边形 OABC 为长方形,OA=10,OC=4,点 D是 OA 的中点, 点 P 在线段 BC 上运动. (1)写出点 A,B,C 的坐标; (2)当△ODP 是腰长为 5 的等腰三角形时,求点 P的坐标. 3.解答下列各题. (1)如图 1,点 P 是∠AOB 的内部任意一点,PM⊥OA,PN⊥OB,垂足分别是 M、N,D 是 OP 的中点.求证:∠MDN=2∠MON. (2)如图 2,若 P 是∠AOB 的外部任意一点,PM⊥OA,PN⊥OB,垂足分别是 M、N,D 是 OP 的中点,问∠MDN 与∠MON 有何数量关系,并说明理由. 4.在△ABC 中,AB=AC,点 D、O 分别是 BC、AC 边的中点,连接 AD,过点 A 作 AE∥BC,交 射线 DO 于点 E,连接 CE. (1)如图 1,求证:四边形 ADCE 是矩形; (2)如图 2,点 F 在线段 CE 上,连接 AF、DF,在不添加任何字母和辅助线的情况下, 请直接写出四个与四边形 ABDF 面积相等的三角形或四边形. 5.已知:△ABC 中,AB=BC,过 A点作 BC 的平行线与∠ABC 的平分线交于点 D,连接 CD. (1)求证:四边形 ABCD 是菱形; (2)连接 AC 与 BD 交于点 O,过点 D 作 DE⊥BC 的延长线于点 E,连接 OE,若∠ABC=60°, BC=6,求 OE 的长. 二.相似综合 1.如图,已知正方形 ABCD,E 是 AB 的中点,F是 AD 上的一点,EG⊥CF 于 G 且 AF= AD. (1)求证:CE 平分∠BCF. (2)求证: AB2 =CG•FG. 2.四边形 ABCD 是正方形,点 E在边 CD 上(不与端点 B,C 重合),点 F 在对角线 AC 上, 且 EF⊥AC,连接 AE (1)如图 1,若 AB=2,当 AE 平分∠DAC 时,求 EC 的长; (2)如图 2,点 G是 AE 的中点,连接 DG,FB,求证:FB= DG. 3.如图,正方形 ABCD 的边长为 8 厘米,动点 P从点 A 出发沿 AB 边由 A向 B以 1厘米/秒的 速度匀速移动(点 P 不与点 A、B重合),动点 Q 从点 B出发沿折线 BC﹣CD 以 2 厘米/秒 的速度匀速移动,点 P、Q 同时出发,当点 P 停止运动,点 Q 也随之停止.连接 AQ,交 BD 于点 E.设点 P 运动时间为 x 秒. (1)当点 Q 在线段 BC 上运动时,点 P 出发多少时间后,∠BEP 和∠BEQ 相等; (2)当点 Q 在线段 BC 上运动时,求证:△BQE 的面积是△APE 的面积的 2倍; (3)设△APE 的面积为 y,试求出 y 关于 x 的函数解析式,并写出函数的定义域. 4.如图,P 为正方形 ABCD 边 BC 上任一点,BG⊥AP 于点 G,在 AP 的延长线上取点 E,使 AG =GE,连接 BE,CE. (1)求证:BE=BC; (2)∠CBE 的平分线交 AE 于 N 点,连接 DN,求证: ; (3)若正方形的边长为 2,当 P点为 BC 的中点时,请直接写出 CE 的长为 . 5.如图,BM、DN 分别平分正方形 ABCD 的两个外角,且∠MAN=45°,连接 MN. (1)猜想以线段 BM、DN、MN 为三边组成的三角形的形状,并证明你的结论; (2)若△AMN 为等腰直角三角形,探究线段 BM、DN 之间的数量关系; (3)当 MN∥AD 时,直接写出 的值. 三.反比例函数综合 1.如图在平面直角坐标系中,O 为原点,A、B 两点分别在 y 轴、x 轴的正半轴上,△AOB 的一条内角平分线、一条外角平分线交于点 P,P 在反比例函数 y= 的图象上. (1)求点 P 的坐标; (2)若 OA=OB,则: ①∠P的度数为 ; ②求出此时直线 AB 的函数关系式; (3)如果直线 AB 的关系式为 y=kx+n,且 0<n<2,作反比例函数 y=﹣ ,过点(0, 1)作 x 轴的平行线与 y= 的图象交于点 M,与 y=﹣ 的图象交于点 N,过点 N 作 y 轴 的平行线与 y=kx+n 的图象交于点 Q,是否存在 k 的值,使得 MN+QN 的和始终是一个定值 d,若存在,求出 k的值及定值 d;若不存在,请说明理由. 2.如图①,已知点 A(﹣1,0),B(0,﹣2),▱ABCD 的边 AD 与 y轴交于点 E,且 E 为 AD 的中点,双曲线 y= 经过 C、D两点. (1)求 k的值; (2)点 P在双曲线 y= 上,点 Q 在 y 轴上,若以点 A、B、P、Q 为顶点的四边形是平行 四边形,直接写出满足要求的所有点 Q 的坐标; (3)以线段 AB 为对角线作正方形 AFBH(如图③),点 T 是边 AF 上一动点,M 是 HT 的 中点,MN⊥HT,交 AB 于 N,当点 T 在 AF 上运动时, 的值是否发生改变?若改变,求 出其变化范围:若不改变,请求出其值,并给出你的证明. 3.如图 1,在平面直角坐标系 xOy 中,双曲线 与直线 y=ax+b(a≠0)交于 A、 B 两点,直线 AB 分别交 x 轴、y 轴于 C、D 两点,E 为 x 轴上一点.已知 OA=OC=OE,A 点坐标为(3,4). (1)将线段 OE 沿 x 轴平移得线段 O′E′(如图 1),在移动过程中,是否存在某个位 置使|BO′﹣AE′|的值最大?若存在,求出|BO′﹣AE′|的最大值及此时点 O′的坐标; 若不存在,请说明理由; (2)将直线 OA 沿射线 OE 平移,平移过程中交 的图象于点 M(M 不与 A 重 合),交 x 轴于点 N(如图 3).在平移过程中,是否存在某个位置使△MNE 为以 MN 为腰 的等腰三角形?若存在,求出 M 的坐标;若不存在,请说明理由. 4.如图,在平面直角坐标系中,OA⊥OB,AB⊥x轴于点 C,点 A( ,1)在反比例函数 y = 的图象上. (1)求反比例函数 y= 的表达式; (2)求△AOB 的面积; (3)在坐标轴上是否存在一点 P,使得以 O、B、P 三点为顶点的三角形是等腰三角形若 存在,请直接写出所有符合条件的点 P 的坐标;若不存在,简述你的理由. 5.如图,过原点的直线 l 与双曲线 y= 相交于 A(2,2)、B 两点,点 C、D 在第三象限 双曲线的图象上(点 C在点 D 上方),连接 AC 交 x 轴于点 E,连接 AD 交 y轴于点 F.设 点 C 的横坐标为 m. (1)用含 m 的代数式表示点 E 的坐标; (2)求证:∠ACB=2∠AEO; (3)若∠CBD=135°,△AEF 的面积为 10,求直线 AC 的表达式.查看更多