2010中考数学兰州考试试题

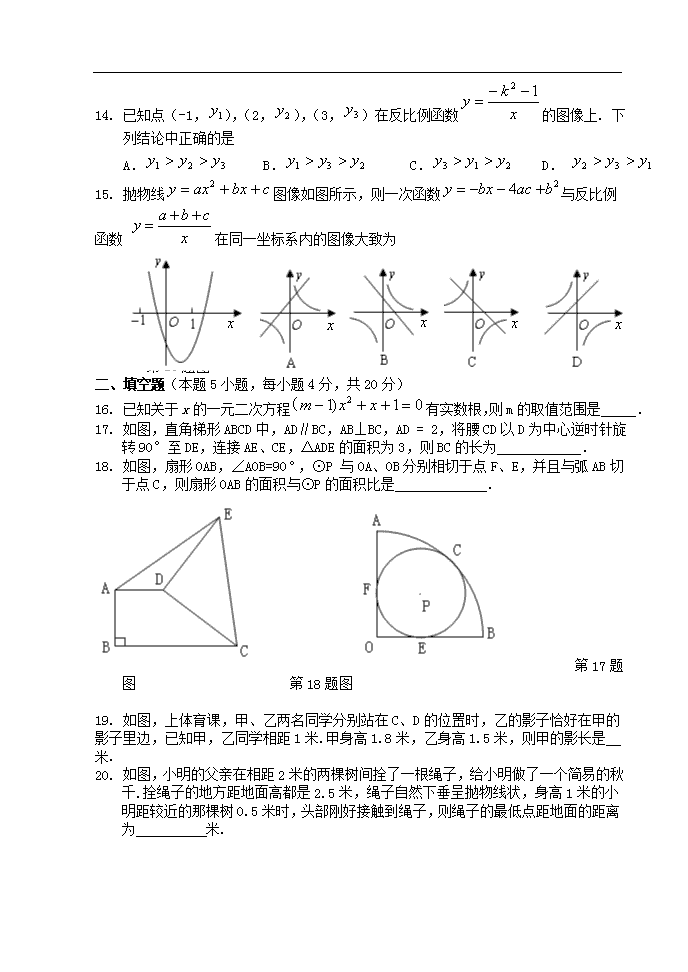
2010中考数学兰州考试试题

‎2010年兰州中考试卷 兰州市2010年初中毕业生学业考试试卷 ‎ 数 学（A）‎ 注意事项：‎ ‎1.全卷共150分，考试时间120分钟。‎ ‎2.考生必须将报考学校、姓名、准考证号、考场、座位号等个人信息填（涂）写在答题卡的相应位置上。‎ ‎3.考生务必将答案直接填（涂）写在答题卡的相应位置上。‎ 一、选择题 (本题15小题，每小题4分，共60分. 在每小题给出的四个选项中，只有一项是符合题目要求的.)‎ ‎ 1. 观察下列银行标志，从图案看既是轴对称图形又是中心对称图形的有 ‎ ‎ ‎ A．1个 B．2个 C．3个 D．4个 ‎2. 函数y ＝＋中自变量x的取值范围是 A．x≤2 B．x＝‎3 C．x＜2且x ≠3 D．x ≤2且x≠3‎ ‎3. 已知一个几何体的三种视图如右图所示，则这个 几何体是 A．圆柱 ‎ ‎ B．圆锥 ‎ C．球体 ‎ ‎ D．正方体 ‎4. 有下列四个命题：①直径是弦；②经过三个点一定可以作圆；③三角形的外心到三角形各顶点的距离都相等；④半径相等的两个半圆是等弧．其中正确的有 ‎ A．4个 B．3个 C． 2个 D． 1个 ‎5. 二次函数的图像的顶点坐标是 ‎ A．（-1，8） B．（1，8） C．（-1，2） D．（1，-4）‎ ‎6. 已知两圆的半径R、r分别为方程的两根，两圆的圆心距为1，两圆的位置关系是 ‎ A．外离 B．内切 C．相交 D．外切 ‎7. 将量角器按如图所示的方式放置在三角形纸板上，使点C在半圆上．点A、B的读数分别为86°、30°，则∠ACB的大小为 A．15 B．‎‎28 C．29 D．34‎ ‎ ‎ 第7题图 第8题图 ‎8. 某射击小组有20人，教练根据他们某次射击的数据绘制成如图所示的统计图. 则这组数据的众数和中位数分别是 ‎ A．7、7 B． 8、7.5 C．7、7.5 D． 8、6‎ ‎9. 现有一个圆心角为，半径为的扇形纸片，用它恰好围成一个圆锥的侧面（接缝忽略不计）.该圆锥底面圆的半径为 A． B． C． D．‎ ‎10. 如图，正三角形的内切圆半径为1，那么这个正三角形的边长为 A． B． C． D． ‎ ‎ ‎ 第10题图 第11题图 ‎11. 如图所示，菱形ABCD的周长为20，DE⊥AB，垂足为E，A=，则下列结论正确的个数有 ‎ ① ② ③菱形的面积为 ④‎ ‎ A． 1个 B． 2个 C． 3个 D． 4个 ‎12. 上海世博会的某纪念品原价168元，连续两次降价%后售价为128元. 下列所列方程中正确的是 ‎ A． B．‎ ‎ C． D．‎ ‎13. 抛物线图像向右平移2个单位再向下平移3个单位，所得图像的解析式为，则b、c的值为 ‎ A . b=2， c=2 B. b=2，c=0 ‎ ‎ C . b= -2，c=-1 D. b= -3， c=2‎ ‎14. 已知点（-1，），（2，），（3，）在反比例函数的图像上. 下列结论中正确的是 ‎ A． B． C． D． ‎ ‎15. 抛物线图像如图所示，则一次函数与反比例函数 在同一坐标系内的图像大致为 x x x x x 第15题图 二、填空题（本题5小题，每小题4分，共20分）‎ ‎16. 已知关于x的一元二次方程有实数根，则m的取值范围是 ． ‎ ‎17. 如图，直角梯形ABCD中，AD∥BC，AB⊥BC，AD = 2，将腰CD以D为中心逆时针旋转90°至DE，连接AE、CE，△ADE的面积为3，则BC的长为 ．‎ ‎18. 如图，扇形OAB，∠AOB=90，⊙P 与OA、OB分别相切于点F、E，并且与弧AB切于点C，则扇形OAB的面积与⊙P的面积比是 ．‎ ‎ ‎ ‎ 第17题图 第18题图 ‎19. 如图，上体育课，甲、乙两名同学分别站在C、D的位置时，乙的影子恰好在甲的影子里边，已知甲，乙同学相距1米.甲身高1.8米，乙身高1.5米，则甲的影长是 米.‎ ‎20. 如图，小明的父亲在相距2米的两棵树间拴了一根绳子，给小明做了一个简易的秋千.拴绳子的地方距地面高都是2.5米，绳子自然下垂呈抛物线状，身高1米的小明距较近的那棵树0.5米时，头部刚好接触到绳子，则绳子的最低点距地面的距离为 米.‎ ‎ 第19题图 第20题图 三、解答题（本题8小题，共70分.解答时写出必要的文字说明、证明过程或演算步骤.）‎ ‎21.（本题满分10分）‎ ‎（1）（本小题满分4分）—+‎ ‎（2）（本小题满分6分） 已知：y＝y1＋y2，y1与x2成正比例，y2与x成反比例，且x＝1时，y＝3；x＝-1时，y＝1. 求x＝-时，y的值．‎ ‎22.（本题满分6分）小明家的房前有一块矩形的空地，空地上有三棵树A、B、C，小明想建一个圆形花坛，使三棵树都在花坛的边上．‎ ‎（1）（本小题满分4分）请你帮小明把花坛的位置画出来（尺规作图，不写作法，保留作图痕迹）．‎ ‎（2）（本小题满分2分））若△ABC中AB=8米，AC=6米，∠BAC=，试求小明家圆形花坛的面积．‎ 第 22题图 ‎23.（本题满分6分）小莉的爸爸买了今年七月份去上海看世博会的一张门票，她和哥哥两人都很想去观看，可门票只有一张，读九年级的哥哥想了一个办法，拿了八张扑克牌，将数字为1，2，3，5的四张牌给小莉，将数字为4，6，7，8的四张牌留给自己，并按如下游戏规则进行：小莉和哥哥从各自的四张牌中随机抽出一张，然后将抽出的两张扑克牌数字相加，如果和为偶数，则小莉去；如果和为奇数，则哥哥去．‎ ‎（1）请用数状图或列表的方法求小莉去上海看世博会的概率；‎ ‎（2）哥哥设计的游戏规则公平吗？若公平，请说明理由；若不公平，请你设计一种公平的游戏规则．‎ ‎24.（本题满分8分）如图是某货站传送货物的平面示意图. 为了提高传送过程的安全性，工人师傅欲减小传送带与地面的夹角，使其由45°改为30°. 已知原传送带AB长为4米.‎ ‎（1）求新传送带AC的长度；‎ ‎（2）如果需要在货物着地点C的左侧留出2米的通道，试判断距离B点4米的货物MNQP是否需要挪走，并说明理由．(说明：⑴⑵的计算结果精确到0.1米，参考数据：≈1.41，≈1.73，≈2.24，≈2.45)‎ 第24题图 ‎25.（本题满分9分）如图，P1是反比例函数在第一象限图像上的一点，点A1 的坐标为(2，0)．‎ ‎ （1）当点P1的横坐标逐渐增大时，△P1O A1的面积 ‎ ‎ 将如何变化？‎ ‎ （2）若△P1O A1与△P2 A1 A2均为等边三角形，求 此反比例函数的解析式及A2点的坐标．‎ 第25题图 ‎26.（本题满分10分）如图，已知AB是⊙O的直径，点C在⊙O上，过点C的直线与AB的延长线交于点P，AC=PC，∠COB=2∠PCB.‎ ‎ （1）求证：PC是⊙O的切线；‎ ‎ （2）求证：BC=AB；‎ ‎ （3）点M是弧AB的中点，CM交AB于点N，若AB=4，求MN·MC的值.‎ 第26题图 ‎ ‎27.（本题满分10分）已知平行四边形ABCD中，对角线AC和BD相交于点O，AC=10， ‎ BD=8．‎ ‎ （1）若AC⊥BD，试求四边形ABCD的面积 ；‎ ‎（2）若AC与BD的夹角∠AOD=，求四边形ABCD的面积；‎ ‎ （3）试讨论：若把题目中“平行四边形ABCD”改为“四边形ABCD”，且∠AOD=‎ AC=，BD=，试求四边形ABCD的面积（用含，，的代数式表示）．‎ 第 27题图 ‎28.（本题满分11分）如图1，已知矩形ABCD的顶点A与点O重合，AD、AB分别在x轴、y轴上，且AD=2，AB=3；抛物线经过坐标原点O和x轴上另一点E（4,0）‎ ‎（1）当x取何值时，该抛物线的最大值是多少？‎ ‎（2）将矩形ABCD以每秒1个单位长度的速度从图1所示的位置沿x轴的正方向匀速平行移动，同时一动点P也以相同的速度从点A出发向B匀速移动.设它们运动的时间为t秒（0≤t≤3），直线AB与该抛物线的交点为N（如图2所示）. ‎ ‎① 当时，判断点P是否在直线ME上，并说明理由；‎ ‎② 以P、N、C、D为顶点的多边形面积是否可能为5，若有可能，求出此时N点的坐标；若无可能，请说明理由．‎ 图1 第28题图 图2‎ 兰州市2010年初中毕业生学业考试试卷 ‎ 数学(A)参考答案及评分标准 一、 选择题（本题15小题，每小题4分，共60分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ ‎13‎ ‎14‎ ‎15‎ 答案 B A B B A B B C C D C B B B D 二、填空题（本题5小题，每小题4分，共20分）‎ ‎16．且m≠1 17．5 18． ‎ ‎19．6 20．‎ 三、解答题（本题8小题，共70分。解答时写出必要的文字说明、证明过程或演算步骤。）‎ ‎21.（本题满分10分）‎ ‎（1）（本小题满分4分）‎ ‎ 解：原式= ……………………………………………2分 ‎ = ………………………………………………………3分 ‎ =5 …………………………………………………………………………4分 ‎（2）（本小题满分6分）‎ ‎ 解：解：y1与x2成正比例，y2与x成反比例 ‎　　设y1＝k1x2，y2＝，y＝k1x2＋…………………………………………………2分 把x＝1，y＝3，x＝-1，y＝1分别代入上式得 ……………………3分 ‎　　　 ∴　 …………………………………………5分 当x＝-,　y＝2×(-)2＋＝-2＝- ………………………………6分 ‎22. （本题满分6分）‎ ‎(1)（本小题满分4分）‎ 用尺规作出两边的垂直平分线 …………………2‎ 分 作出圆 …………………………3分 ‎⊙O即为所求做的花园的位置.（图略） ……………………………4分 ‎（2）（本小题满分2分）‎ ‎ 解：∵∠BAC=,AB=‎8米,AC=‎6米, ∴BC=‎‎10米 ‎ ∴ △ABC外接圆的半径为‎5米 ……………………………………5分 ‎ ∴小明家圆形花坛的面积为2平方米 . …………………………… 6分 ‎23.（本题满分6分）‎ ‎ (1)所有可能的结果如有表：‎ 一共有16种结果，每种结果出现的 可能性相同．‎ ‎…………………………………2分 和为偶数的概率为 ‎ 所以小莉去上海看世博会的概率为 ………………………………3分 ‎(2)由（1）列表的结果可知：小莉去的概率为，哥哥去的概率为，所以游戏 不公平，对哥哥有利． …………………………………………4分 ‎ 游戏规则改为：若和为偶数则小莉得5分，若和为奇数则哥哥得3分，则游戏是 公平的． ……………………………………………………6分 ‎ （游戏规则的修改有多种多样，阅卷老师视情况给分）‎ ‎24.（本题满分8分）‎ ‎ （1）如图，作AD⊥BC于点D ……………………………………1分 Rt△ABD中， ‎ AD=ABsin45°=4……2分 ‎ 在Rt△ACD中，∵∠ACD=30°‎ ‎∴AC=2AD=≈………………………3分 ‎ 即新传送带AC的长度约为米． ………………………………………4分 ‎（2）结论：货物MNQP应挪走． ……………………………………5分 解：在Rt△ABD中，BD=ABcos45°=4 ……………………6分 ‎ 在Rt△ACD中，CD=AC cos30°=‎ ‎ ∴CB=CD—BD=≈2.1 ‎ ‎∵PC=PB—CB ≈4—2.1=1.9＜2 ………………………………7分 ‎ ∴货物MNQP应挪走． …………………………………………………………8分 ‎25. （本题满分9分）‎ ‎（1）解：（1）△P1OA1的面积将逐渐减小． …………………………………2分 ‎（2）作P‎1C⊥OA1，垂足为C，因为△P1O A1为等边三角形，‎ 所以OC=1，P‎1C=，所以P1． ……………………………………3分 代入，得k=，所以反比例函数的解析式为． ……………4分 作P2D⊥A‎1 A2，垂足为D、设A1D=a，则OD=2+a，P2D=a，‎ 所以P2． ……………………………………………………………6分 代入，得，化简得 解的：a=-1± ……………………………………………7分 ‎∵a＞0 ∴ ………………………………8分 所以点A2的坐标为﹙，0﹚ ………………………………………………9分 ‎26. （本题满分10分）‎ 解：（1）∵OA=OC,∴∠A=∠ACO ‎ ‎ ∵∠COB=2∠A ,∠COB=2∠PCB ‎ ‎ ∴∠A=∠ACO=∠PCB ……………………………………………………1分 ‎ ∵AB是⊙O的直径 ‎ ∴∠ACO+∠OCB=90° …………………………………………………2分 ‎ ∴∠PCB+∠OCB=90°,即OC⊥CP …………………………………………3分 ‎∵OC是⊙O的半径 ‎ ‎ ∴PC是⊙O的切线 …………………………………………………4分 ‎ （2）∵PC=AC ∴∠A=∠P ‎ ∴∠A=∠ACO=∠PCB=∠P ‎ ‎ ∵∠COB=∠A+∠ACO,∠CBO=∠P+∠PCB ‎ ∴∠CBO=∠COB ……………………………………………5分 ‎ ∴BC=OC ‎ ∴BC=AB ………………………………………………………6分 ‎ (3)连接MA,MB ‎ ‎ ∵点M是弧AB的中点 ‎ ∴弧AM=弧BM ∴∠ACM=∠BCM ………7分 ‎ ‎∵∠ACM=∠ABM ∴∠BCM=∠ABM ‎ ‎ ∵∠BMC=∠BMN ‎ ∴△MBN∽△MCB ‎ ‎ ∴ ‎ ‎∴BM2=MC·MN ……………………8分 ‎ ∵AB是⊙O的直径，弧AM=弧BM ‎ ‎ ∴∠AMB=90°,AM=BM ‎ ∵AB=4 ∴BM= ………………………………………………………9分 ‎ ∴MC·MN=BM2=8 ……………………………………………………10分 ‎27. （本题满分10分）‎ ‎ ‎ ‎ 解：（1）∵AC⊥BD ‎∴四边形ABCD的面积 ‎ ‎ ‎ ‎ ‎ ‎ ………………………………………2分 ‎ ‎ ‎（2）过点A分别作AE⊥BD，垂足为E …………………………………3分 ‎∵四边形ABCD为平行四边形 ‎ ‎ 在Rt⊿AOE中，‎ ‎ ∴ …………4分 ‎ ∴ ………………………………5分 ‎ ∴四边形ABCD的面积 ……………………………………6分 ‎ (3）如图所示过点A,C分别作AE⊥BD，CF⊥BD，垂足分别为E,F …………7分 ‎ 在Rt⊿AOE中，‎ ‎ ∴‎ ‎ 同理可得 ‎ ‎ ………………………………8分 ‎ ‎ ‎…………………………………10分 ‎ ‎∴四边形ABCD的面积 ‎28. （本题满分11分）‎ ‎ 解：（1）因抛物线经过坐标原点O（0,0）和点E（4,0）‎ 故可得c=0,b=4‎ 所以抛物线的解析式为…………………………………………1分 由 得当x=2时，该抛物线的最大值是4. …………………………………………2分 ‎（2）① 点P不在直线ME上. ‎ 已知M点的坐标为(2,4)，E点的坐标为(4,0)，‎ 设直线ME的关系式为y=kx+b.‎ 于是得 ，解得 所以直线ME的关系式为y=-2x+8. …………………………………………3分 由已知条件易得，当时，OA=AP=，…………………4分 ‎∵ P点的坐标不满足直线ME的关系式y=-2x+8. [来源:Zxxk.Com]‎ ‎∴ 当时，点P不在直线ME上. ……………………………………5分 ‎②以P、N、C、D为顶点的多边形面积可能为5‎ ‎∵ 点A在x轴的非负半轴上，且N在抛物线上， ‎ ‎∴ OA=AP=t.‎ ‎∴ 点P，N的坐标分别为(t,t)、(t,-t 2+4t) …………………………………6分 ‎∴ AN=-t 2+4t (0≤t≤3) ,‎ ‎∴ AN-AP=(-t 2+4 t)- t=-t 2+3 t=t(3-t)≥0 , ∴ PN=-t 2+3 t ‎ ‎…………………………………………………………………………………7分 ‎（ⅰ）当PN=0，即t=0或t=3时，以点P，N，C，D为顶点的多边形是三角形，此三角形的高为AD，∴ S=DC·AD=×3×2=3. ‎ ‎（ⅱ）当PN≠0时，以点P，N，C，D为顶点的多边形是四边形 ‎∵ PN∥CD，AD⊥CD，‎ ‎∴ S=(CD+PN)·AD=[3+(-t 2+3 t)]×2=-t 2+3 t+3…………………8分 当-t 2+3 t+3=5时，解得t=1、2…………………………………………………9分 ‎ 而1、2都在0≤t≤3范围内，故以P、N、C、D为顶点的多边形面积为5‎ 综上所述，当t=1、2时，以点P，N，C，D为顶点的多边形面积为5，‎ 当t=1时，此时N点的坐标（1,3）………………………………………10分 当t=2时，此时N点的坐标（2,4）………………………………………11分 说明：（ⅱ）中的关系式，当t=0和t=3时也适合.（故在阅卷时没有（ⅰ ‎），只有（ⅱ）也可以,不扣分）‎