2013年辽宁省锦州市中考数学试卷（含答案）

2013年辽宁省锦州市中考数学试卷（含答案）

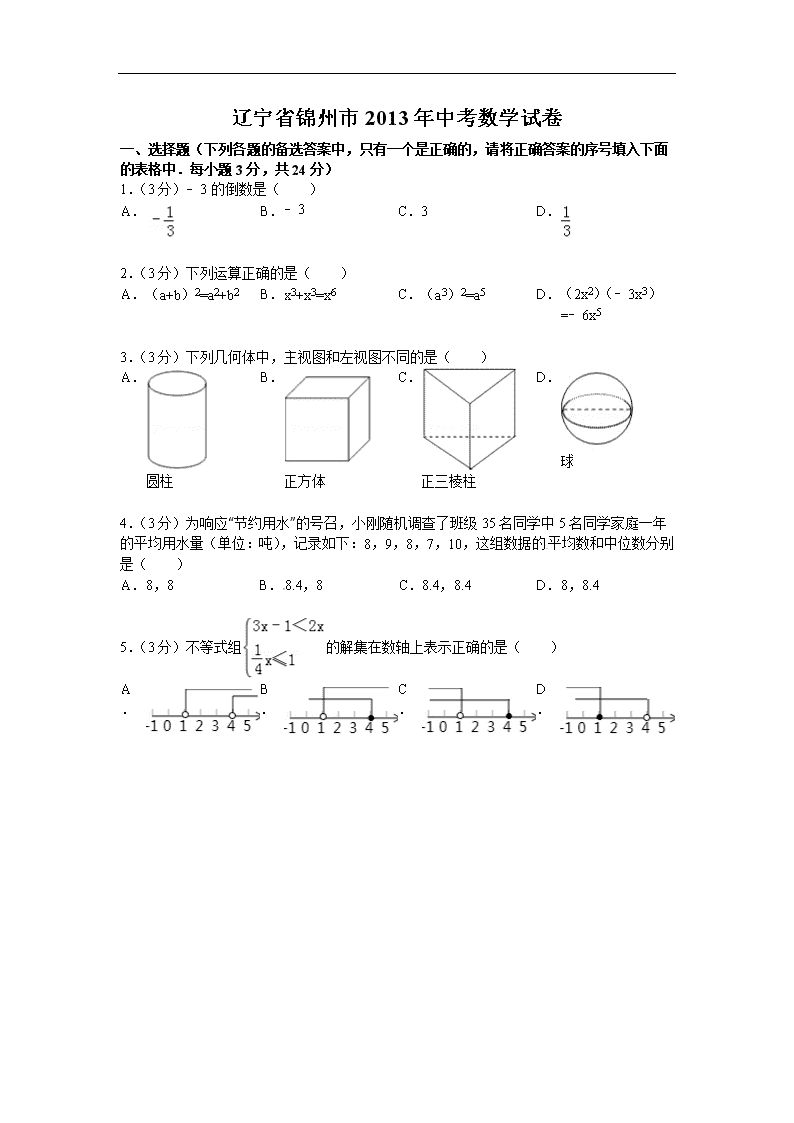
辽宁省锦州市2013年中考数学试卷 一、选择题（下列各题的备选答案中，只有一个是正确的，请将正确答案的序号填入下面的表格中．每小题3分，共24分）‎ ‎1．（3分）﹣3的倒数是（　　）‎ ‎　‎ A．‎ B．‎ ‎﹣3‎ C．‎ ‎3‎ D．‎ ‎　‎ ‎2．（3分）下列运算正确的是（　　）‎ ‎　‎ A．‎ ‎（a+b）2=a2+b2‎ B．‎ x3+x3=x6‎ C．‎ ‎（a3）2=a5‎ D．‎ ‎（2x2）（﹣3x3）=﹣6x5‎ ‎　‎ ‎3．（3分）下列几何体中，主视图和左视图不同的是（　　）‎ ‎　‎ A．‎ 圆柱 B．‎ 正方体 C．‎ 正三棱柱 D．‎ 球 ‎　‎ ‎4．（3分）为响应“节约用水”的号召，小刚随机调查了班级35名同学中5名同学家庭一年的平均用水量（单位：吨），记录如下：8，9，8，7，10，这组数据的平均数和中位数分别是（　　）‎ ‎　‎ A．‎ ‎8，8‎ B．‎ ‎8.4，8‎ C．‎ ‎8.4，8.4‎ D．‎ ‎8，8.4‎ ‎　‎ ‎5．（3分）不等式组的解集在数轴上表示正确的是（　　）‎ ‎　‎ A．‎ B．‎ C．‎ D．‎ ‎　‎ ‎6．（3分）如图，直线y=mx与双曲线y=交于A，B两点，过点A作AM⊥x轴，垂足为点M，连接BM，若S△ABM=2，则k的值为（　　）‎ ‎　‎ A．‎ ‎﹣2‎ B．‎ ‎2‎ C．‎ ‎4‎ D．‎ ‎﹣4‎ ‎　‎ ‎7．（3分）有如下四个命题：‎ ‎（1）三角形有且只有一个内切圆；‎ ‎（2）四边形的内角和与外角和相等；‎ ‎（3）顺次连接四边形各边中点所得的四边形一定是菱形；‎ ‎（4）一组对边平行且一组对角相等的四边形是平行四边形．‎ 其中真命题的个数有（　　）‎ ‎　‎ A．‎ ‎1个 B．‎ ‎2个 C．‎ ‎3个 D．‎ ‎4个 ‎　‎ ‎8．（3分）为了帮助遭受自然灾害的地区重建家园，某学校号召同学们自愿捐款．已知第一次捐款总额为4800元，第二次捐款总额为5000元，第二次捐款人数比第一次多20人，而且两次人均捐款额恰好相等，如果设第一次捐款人数是x人，那么x满足的方程是（　　）‎ ‎　‎ A．‎ B．‎ ‎=‎ C．‎ D．‎ ‎　‎ 二、填空题（本大题共8个小题，每小题3分，共24分）‎ ‎9．（3分）分解因式x3﹣xy2的结果是　x（x+y）（x﹣y）　．‎ ‎　[来源:学科网ZXXK]‎ ‎10．（3分）函数中，自变量x的取值范围是　x≥2　．‎ ‎　‎ ‎11．（3分）据统计，2013锦州世界园林博览会6月1日共接待游客约154000人次，154000可用科学记数法表示为　1.54×105　．‎ ‎　‎ ‎12．（3分）为从甲、乙、丙三名射击运动员中选一人参加全运会，教练把他们的10次比赛成绩作了统计：平均成绩为9.3环：方差分别为S2甲=1.22，S2乙=1.68，S2丙=0.44，则应该选　丙　参加全运会．‎ ‎　‎ ‎13．（3分）计算：|1﹣|+﹣（3.14﹣π）0﹣（﹣）﹣1=　3　．‎ ‎　‎ ‎14．（3分）在四张背面完全相同的卡片正面分别画有正三角形，正六边形、平行四边形和圆，将这四张卡片背面朝上放在桌面上．现从中随机抽取一张，抽出的图形是中心对称图形的概率是　　．‎ ‎　‎ ‎15．（3分）在△ABC中，AB=AC，AB的垂直平分线DE与AC所在的直线相交于点E，垂足为D，连接BE．已知AE=5，tan∠AED=，则BE+CE=　6或16　．　‎ ‎16．（3分）二次函数y=的图象如图，点A0位于坐标原点，点A1，A2，A3…An在y轴的正半轴上，点B1，B2，B3…Bn在二次函数位于第一象限的图象上，点C1，C2，C3…Cn在二次函数位于第二象限的图象上，四边形A0B1A1C1，四边形A1B2A2C2，四边形A2B3A3C3…四边形An﹣1BnAnCn都是菱形，∠A0B1A1=∠A1B2A1=∠A2B3A3…=∠An﹣1BnAn=60°，菱形An﹣1BnAnCn的周长为　4n　．‎ ‎　‎ 三、解答题（本大题共2个小题，每小题8分，共16分）‎ ‎17．（8分）先将（1﹣）÷化简，然后请自选一个你喜欢的x值代入求值．‎ ‎　‎ ‎18．（8分）如图，方格纸中的每个小正方形边长都是1个长度单位，Rt△ABC的顶点均在格点上，建立平面直角坐标系后，点A的坐标为（1，1），点B的坐标为（4，1）．‎ ‎（1）先将Rt△ABC向左平移5个单位长度，再向下平移1个单位长度得到Rt△A1B1C1，试在图中画出Rt△A1B1C1，并写出点A1的坐标；‎ ‎（2）再将Rt△A1B1C1绕点A1顺时针旋转90°后得到Rt△A2B2C2，试在图中画出Rt△A2B2C2，并计算Rt△A1B1C1在上述旋转过程中点C1所经过的路径长．‎ ‎　‎ 四、解答题（本大题共2小题，每小题10分，共20分）‎ ‎19．（10分）以下是根据全国人力资源和社会保障部公布的相关数据绘制的统计图的一部分，请你根据图中信息解答下列问题：‎ ‎（1）求2013年全国普通高校毕业生数年增长率约是多少？（精确到0.1%）‎ ‎（2）求2011年全国普通高校毕业生数约是多少万人？（精确到万位）‎ ‎（3）补全折线统计图和条形统计图．‎ ‎　‎ ‎20．（10分）如图，点O是菱形ABCD对角线的交点，DE∥AC，CE∥BD，连接OE．‎ 求证：OE=BC．‎ 五、解答题（本大题共2个小题，每小题10分，共20分）‎ ‎21．（10分）一个不透明的口袋中装有4个完全相同的小球，分别标有数字1、2、3、4，另有一个可以自由旋转的圆盘．被分成面积相等的3个扇形区，分别标有数字1、2、3（如图所示）．小颖和小亮想通过游戏来决定谁代表学校参加歌咏比赛，游戏规则为：一人从口袋中摸出一个小球，另一个人转动圆盘，如果所摸球上的数字与圆盘上转出数字之和小于4，那么小颖去；否则小亮去．‎ ‎（1）用树状图或列表法求出小颖参加比赛的概率；‎ ‎（2）你认为该游戏公平吗？请说明理由；若不公平，请修改该游戏规则，使游戏公平．‎ ‎　‎ ‎22．（10分）如图，某公司入口处有一斜坡AB，坡角为12°，AB的长为3m，施工队准备将斜坡修成三级台阶，台阶高度均为hcm，深度均为30cm，设台阶的起点为C．‎ ‎（1）求AC的长度；‎ ‎（2）求每级台阶的高度h．‎ ‎（参考数据：sin12°≈0.2079，cos12°≈0.9781，tan12°≈0.2126．结果都精确到0.1cm）‎ ‎　‎ 六、解答题（本大题共2个小题，每小题10分，共20分）‎ ‎23．（10分）如图，AB是⊙O的直径，C是⊙O上一点，OD⊥BC于点D，过点C作⊙O的切线，交OD的延长线于点E，连接BE．‎ ‎（1）求证：BE与⊙O相切；‎ ‎（2）设OE交⊙O于点F，若DF=1，BC=2，求由劣弧BC、线段CE和BE所围成的图形面积S．‎ ‎　‎ ‎24．（10分）甲、乙两车分别从A，B两地同时出发相向而行．并以各自的速度匀速行驶，甲车途径C地时休息一小时，然后按原速度继续前进到达B地；乙车从B地直接到达A地，如图是甲、乙两车和B地的距离y（千米）与甲车出发时间x（小时）的函数图象．‎ ‎（1）直接写出a，m，n的值；‎ ‎（2）求出甲车与B地的距离y（千米）与甲车出发时间x（小时）的函数关系式（写出自变量x的取值范围）；‎ ‎（3）当两车相距120千米时，乙车行驶了多长时间？‎ ‎　‎ 七、解答题（本题12分）‎ ‎25．（12分）如图1，等腰直角三角板的一个锐角顶点与正方形ABCD的顶点A重合，将此三角板绕点A旋转，使三角板中该锐角的两条边分别交正方形的两边BC，DC于点E，F，连接EF．‎ ‎（1）猜想BE、EF、DF三条线段之间的数量关系，并证明你的猜想；‎ ‎（2）在图1中，过点A作AM⊥EF于点M，请直接写出AM和AB的数量关系；‎ ‎（3）如图2，将Rt△ABC沿斜边AC翻折得到Rt△ADC，E，F分别是BC，CD边上的点，∠EAF=∠BAD，连接EF，过点A作AM⊥EF于点M，试猜想AM与AB之间的数量关系．并证明你的猜想．‎ ‎　‎ 八、解答题（本题14分）‎ ‎26．（14分）如图，抛物线y=﹣x2+mx+n经过△ABC的三个顶点，点A坐标为（0，3），点B坐标为（2，3），点C在x轴的正半轴上．‎ ‎（1）求该抛物线的函数关系表达式及点C的坐标；‎ ‎（2）点E为线段OC上一动点，以OE为边在第一象限内作正方形OEFG，当正方形的顶点F恰好落在线段AC上时，求线段OE的长；‎ ‎（3）将（2）中的正方形OEFG沿OC向右平移，记平移中的正方形OEFG为正方形DEFG，当点E和点C重合时停止运动．设平移的距离为t，正方形DEFG的边EF与AC交于点M，DG所在的直线与AC交于点N，连接DM，是否存在这样的t，使△DMN是等腰三角形？若存在，求出t的值；若不存在，请说明理由；‎ ‎（4）在上述平移过程中，当正方形DEFG与△ABC的重叠部分为五边形时，请直接写出重叠部分的面积S与平移距离t的函数关系式及自变量t的取值范围；并求出当t为何值时，S有最大值，最大值是多少？‎