中考数学复习冲刺专项训练精讲:和圆有关的位置关系教学课件(初三数学章节复习课件)
第六章 圆
和圆有关的位置关系
中考数学复习冲刺专项训练精讲
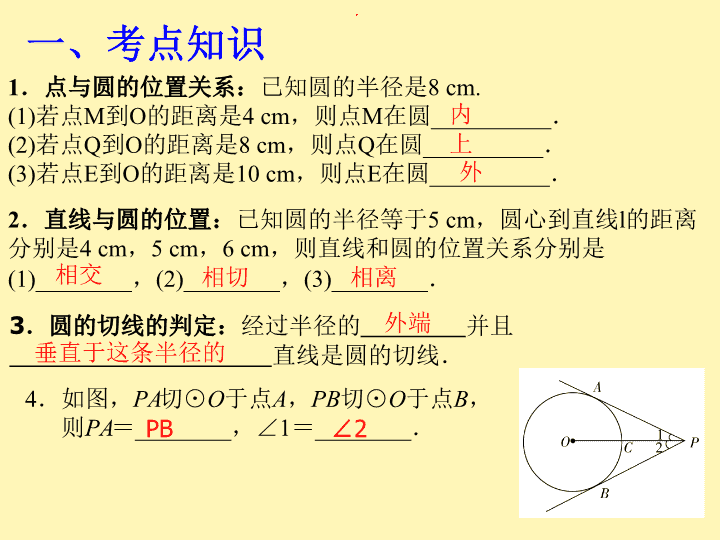
1.点与圆的位置关系:已知圆的半径是8 cm.
(1)若点M到O的距离是4 cm,则点M在圆__________.
(2)若点Q到O的距离是8 cm,则点Q在圆__________.
(3)若点E到O的距离是10 cm,则点E在圆__________.
一、考点知识
,
2.直线与圆的位置:已知圆的半径等于5 cm,圆心到直线l的距离
分别是4 cm,5 cm,6 cm,则直线和圆的位置关系分别是
(1)________,(2)________,(3)________.
内
3.圆的切线的判定:经过半径的________并且
____________________直线是圆的切线.
4.如图,PA切⊙O于点A,PB切⊙O于点B,
则PA=________,∠1=________.
上
外
相交 相切 相离
外端
垂直于这条半径的
PB ∠2
【例1】在△ABC中,∠C=90°,AC=4,CB=3,若以C为
圆心,以r为半径作圆,那么:
(1)当直线AB与⊙ C相离时,r的取值范围是____________;
(2)当直线AB与⊙ C相切时,r的取值范围是________;
(3)当直线AB与⊙ C相交时,r的取值范围是________.
【考点1】直线与圆的位置
二、例题与变式
0
2.4
【变式1】已知,如图,∠AOB=30°,M为OB边上
任意一点,以M为圆心r为半径的⊙ M,当⊙ M与OA相
切时,OM=2 cm,则r=__________cm.1
【考点2】圆的切线的判定
【例2】如图,⊙ O经过菱形ABCD的三个顶点A,
C,D,且与AB相切于点A.求证:BC为⊙ O的切线.
提示:连接OA,OB,OC,
∵⊙ O与AB相切于点A,
∴∠OAB=90°.
易证 △AOB≌ △COB.
∴∠BCO=∠OAB=90°.
∴BC是⊙ O的切线.
【变式2】如图,在△ABC中,AB=BC,以AB
为直径的⊙ O与AC交于点D,过点D作DF⊥BC,交
AB的延长线于点E,垂足为点F,求证:直线DE是
⊙ O的切线 .
证明:连接OD,BD, ∵AB是⊙ O的直径,
∴∠ADB=∠90°. ∴BD⊥AC.
∵AB=BC,∴AD=DC.
∵OA=OB,∴OD∥BC.
∵DE⊥BC,∴DE⊥OD.
∴直线DE是⊙ O的切线.
【考点3】切线长定理
【例3】如图, 已知△ABC,AC=BC=6,∠C=90°.O是
AB的中点,⊙ O与AC,BC分别相切于点D与点E.点F是⊙ O
与AB的一个交点,连DF并延长交CB的延长线于点G,求CG
的长度.
解:连接OD,则OD⊥AC.
∵∠C=90°,∴OD∥CB.
∵O是AB的中点,∴OD是△ABC的中位线,即OD= BC=3.
∵AC=BC=6. ∠C=90°,∴AB= ,则OB= .
∵OD∥CG,∴∠ODF=∠G.
∵OD=OF,则∠ODF=∠OFD. ∴∠BFG=∠OFD=∠G.
∴BF=BG=OB-OF= ,
∴CG=BC+BG= .
1
2
6 2 3 2
3 2 3
3 3 2
【变式3】如图,PA,PB是⊙ O的两条切线,A,B为切点,
求证:∠ABO= ∠APB
证明:连接OP,
∵PA,PB是⊙ O的两条切线,A,B为切点,
∴∠OBP=∠OAP=90°.
又∵OB=OA, OP=OP, ∴BP=AP.
∴△OBP≌ △OAP. ∴∠OPB=∠OPA.
又∵OA=OB. ∴∠OBA=∠OAB.
又∵∠OBA+∠OAB+∠BOA=180°.
∴∠APB+∠BOA=180°.
∴∠OBA+∠OAB=∠APB.
又∠OBA=∠OAB, ∠ABO= ∠APB.
1
2
1
2
A组
1.正方形ABCD的边长为2 cm,以A为圆心2 cm为半径作
⊙ A,则点B在⊙ A________;点C 在⊙ A________;点D
在⊙ A________.
三、过关训练
3.如图,PA,PB是⊙ O的两条切线,切点分别是A,B,∠P=
60°,PA=10,则⊙ O的半径是 ______.
2.已知圆的半径是6.5 cm,圆心到直线l的距离是4.5 cm,那么这
条直线和圆的公共点的个数是________.
上 外
上
两个
5
B组
4.如图,在同一平面直角坐标系中有5个点:
A(1,1),B(-3,-1),C(-3,1),D(-22),
E(0,-3).
(1)用尺规作出△ABC的外接圆⊙ P,并指出点D与⊙ P的
位置关系;
(2)若直线l经过点D(-2,-2),E(0,-3),判断直线l与
⊙ P的位置关系.
解:作图略,点D在⊙ P上.
(2)直线DE与⊙ P相切
5.如图,在Rt△ABC中,∠ACB=90°,以AC为直径作
⊙ O交AB于点D,连接CD.
(1)求证:∠A=∠BCD;
(2)若M为线段BC上一点,试问当点M在什么位置时,直线DM
与⊙ O相切?并说明理由.
证明:(1)∵AC为直径,∴∠ADC=90°.
∴∠A+∠DCA=90°. ∵∠ACB=90°,
∴∠DCB+∠ACD=90°. ∴∠DCB=∠A.
(2)解:当MC=MD(或点M是BC的中点)时,
直线DM与⊙ O相切.理由如下:
连接DO,∵DO=CO,∴∠ODC=∠OCD,
∵DM=CM,∴∠MDC=∠MCD.
∵∠OCD +∠MCD =90°,∴∠ODC +∠MDC =90°.
∴直线DM与⊙ O相切.