2020年江苏省南京市中考数学二模试卷
2020年江苏省南京市中考数学二模试卷
一、单选题
1. 设a是最小的自然数,b是最大的负整数,c是绝对值最小的有理数,a,b,c三个数的和为( )
A.−1 B.0 C.1 D.不存在
2. 已知点P(−1, m2+1)与点Q关于原点对称,则点Q一定在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
3. 若不等式组1
k 有解,则k的取值范围是( )
A.k<2 B.k≥2 C.k<1 D.1≤k<2
4. 如图,二次函数y=ax2+bx+c的图象经过点(1, 1)和点(3, 0).关于这个二次函数的描述:①a<0,b>0,c<0;②当x=2时,y的值等于1;③当x>3时,y的值小于0.正确的是( )
A.①② B.①③ C.②③ D.①②③
5. 计算999−93的结果更接近( )
A.999 B.998 C.996 D.933
6. 如图,点P是⊙O外任意一点,PM、PN分别是⊙O的切线,M、N是切点.设OP与⊙O交于点K.则点K是△PMN的( )
A.三条高线的交点 B.三条中线的交点
C.三个角的角平分线的交点 D.三条边的垂直平分线的交点
二、填空题
−8的立方根是________.
计算:(−2x2y)3=________.
因式分解:a3−ab2=________.
如图,⊙O的半径为2,点A,B在⊙O上,∠AOB=90∘,则阴影部分的面积为________.
直线y=12x与双曲线y=kx在第一象限的交点为(a, 1),则k=________.
已知方程x2−mx−3m=0的两根是x1、x2,若x1+x2=1,则x1x2=________.
如图,若正方形EFGH由正方形ABCD绕图中某点顺时针旋转90∘得到,则旋转中心应该是________点.
如图,在四边形ABCD中,AD // BC,AD=2,AB=22,以点A为圆心,AD为半径的圆与BC相切于点E,交AB于点F,则DF的长为________.
平面直角坐标系中,原点O关于直线y=−43x+4对称点O1的坐标是________.
第21页 共24页 ◎ 第22页 共24页
定点O、P的距离是5,以点O为圆心,一定的长为半径画圆⊙O,过点P作⊙O的两条切线,切点分别是B、C,则线段BC的最大值是________.
三、解答题
先化简,再求值:x2−1x2−2x+1+x2−2xx−2÷x,其中x=3.
(1)解不等式x3−x−12≤1,并把它的解集在数轴上表示出来;
(2)若关于x的一元一次不等式x≥a只有3个负整数解,则a的取值范围是________.
一个不透明箱子中有2个红球,1个黑球和1个白球,四个小球的形状、大小完全相同.
(1)从中随机摸取1个球,则摸到黑球的概率为________.
(2)小明和小贝做摸球游戏,游戏规则如下.
游戏规则
让小明先从箱子中随机摸取
个小球,记下颜色后放回箱子,
摇匀后再让小贝随机摸取一个小
球,记下颜色,若两人所摸小球的
颜色相同,则小明胜:反之,则小
贝胜
你认为这个游戏公平吗?请说明理由.
某工厂有甲、乙两台机器加工同一种零件,已知一小时甲加工的零件数与一小时乙加工的零件数的和为36个,甲加工80个零件与乙加工100个零件的所用时间相等.求甲、乙两台机器每小时分别加工零件多少个?
如图,等腰三角形ABC中,AB=AC.
(1)用尺规作出圆心在直线BC上,且过A、C两点的⊙O;(注:保留作图痕迹,标出点O,并写出作法)
(2)若∠B=30∘,求证:AB与(1)中所作⊙O相切.
现在正是草莓热销的季节,某水果零售商店分两批次从批发市场共购进草莓40箱,已知第一、二次进货价分别为每箱50元、40元,且第二次比第一次多付款700元.
(1)设第一、二次购进草莓的箱数分别为a箱、b箱,求a,b的值;
(2)若商店对这40箱草莓先按每箱60元销售了x箱,其余的按每箱35元全部售完.
①求商店销售完全部草莓所获利润y(元)与x(箱)之间的函数关系式;
②当x的值至少为多少时,商店才不会亏本.
(注:按整箱出售,利润=销售总收入-进货总成本)
某长方体包装盒的表面积为146cm2,其展开图如图所示.求这个包装盒的体积.
如图,已知∠ABM=30∘,AB=20,C是射线BM上一点.
(1)在下列条件中,可以唯一确定BC长的是________;(填写所有符合条件的序号)
①AC=13;②tan∠ACB=125;③△ABC的面积为126.
(2)在(1)的答案中,选择一个作为条件,画出示意图,求BC的长.
某商场经市场调查,发现进价为40元的某童装每月的销售量y(件)与售价x(元)的相关信息如下:
售价x(元)
60
70
80
90
…
销售量y(件)
280
260
240
220
…
(1)试用你学过的函数来描述y与x的关系,这个函数可以是________(填一次函数、反比例函数或二次函数),求这个函数关系式;
(2)售价为多少元时,当月的利润最大?最大利润是多少?
第21页 共24页 ◎ 第22页 共24页
计算
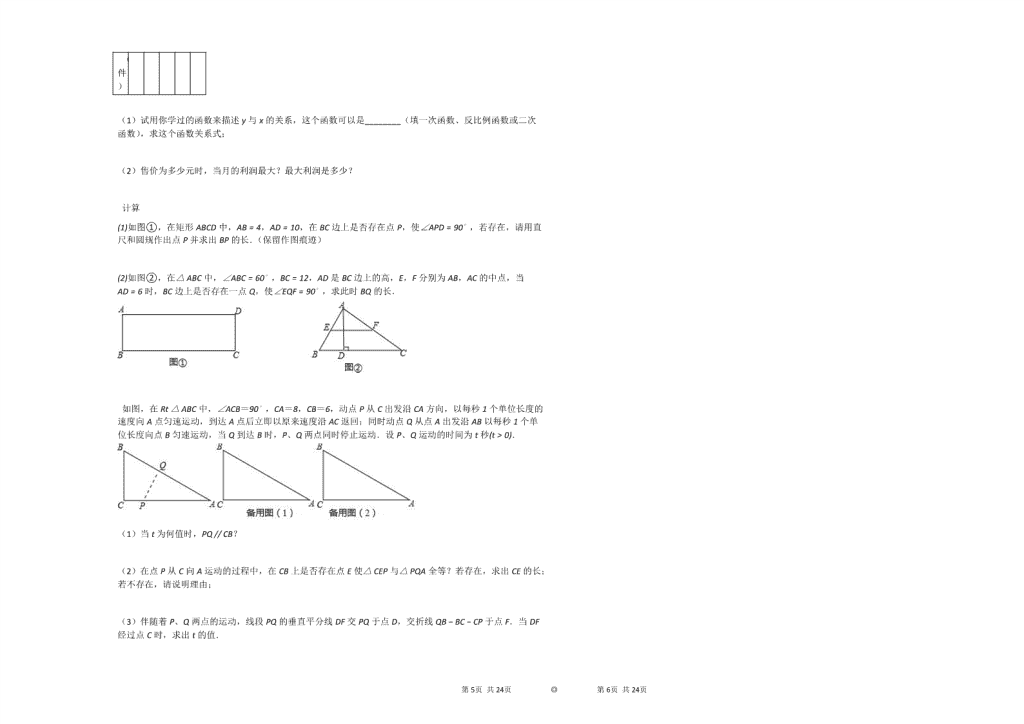
(1)如图①,在矩形ABCD中,AB=4,AD=10,在BC边上是否存在点P,使∠APD=90∘,若存在,请用直尺和圆规作出点P并求出BP的长.(保留作图痕迹)
(2)如图②,在△ABC中,∠ABC=60∘,BC=12,AD是BC边上的高,E,F分别为AB,AC的中点,当AD=6时,BC边上是否存在一点Q,使∠EQF=90∘,求此时BQ的长.
如图,在Rt△ABC中,∠ACB=90∘,CA=8,CB=6,动点P从C出发沿CA方向,以每秒1个单位长度的速度向A点匀速运动,到达A点后立即以原来速度沿AC返回;同时动点Q从点A出发沿AB以每秒1个单位长度向点B匀速运动,当Q到达B时,P、Q两点同时停止运动.设P、Q运动的时间为t秒(t>0).
(1)当t为何值时,PQ // CB?
(2)在点P从C向A运动的过程中,在CB上是否存在点E使△CEP与△PQA全等?若存在,求出CE的长;若不存在,请说明理由;
(3)伴随着P、Q两点的运动,线段PQ的垂直平分线DF交PQ于点D,交折线QB−BC−CP于点F.当DF经过点C时,求出t的值.
第21页 共24页 ◎ 第22页 共24页
参考答案与试题解析
2020年江苏省南京市中考数学二模试卷
一、单选题
1.
【答案】
A
【考点】
有理数的加法
【解析】
先根据自然数,整数,有理数的概念分析出a,b,c的值,再进行计算.
【解答】
∵ 最小的自然数是0,最大的负整数是−1,绝对值最小的有理数是0,
∴ a+b+c=0+(−1)+0=−1.
2.
【答案】
D
【考点】
关于原点对称的点的坐标
【解析】
根据关于原点对称,横纵坐标都互为相反数,进行计算即可.
【解答】
∵ 点P(−1, m2+1)与点Q关于原点对称,
∴ Q(1, −m2−1),
∴ 点Q一定在第四象限,
3.
【答案】
A
【考点】
解一元一次不等式组
【解析】
根据不等式组的解集为两个不等式解集的公共部分,所以在有解的情况下,k的值必须小于2.
【解答】
因为不等式组1k 有解,根据口诀可知k只要小于2即可.
4.
【答案】
B
【考点】
二次函数图象与系数的关系
二次函数图象上点的坐标特征
【解析】
由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
【解答】
①如图所示,抛物线开口方向向下,则a<0.
对称轴在y轴的右侧,则a、b异号,即b>0.
抛物线与y轴交于负半轴,则b<0.
综上所述,a<0,b>0,c<0.
故①正确;
②∵ 抛物线与x轴另一交点横坐标03时,y的值小于0,
故③正确;
5.
【答案】
A
【考点】
因式分解-提公因式法
【解析】
根据因式分解解答即可.
【解答】
999−93=93(996−1)≈999,
6.
【答案】
C
【考点】
切线的性质
【解析】
连接OM、ON、MK、NK,根据切线长定理得出PM=PN,易证得△POM≅△PON,得出OP是∠MPN的平分线,然后根据圆周角定理证得∠PMK=12∠MOK,∠PNK=12∠NOK,∠NMK=12∠NOK,∠MNK=12∠MOK,即可证得∠PMK=∠NMK=∠PNK=∠MNK,从而证得结论.
【解答】
连接OM、ON、MK、NK,
∵ PM、PN分别是⊙O的切线,
∴ PM=PN,
∴ ∠PMN=∠PNM,
∵ OM=ON易证△POM≅△PON,
∴ OP是∠MPN的平分线,
由圆周角定理可得∠PMK=12∠MOK,∠PNK=12∠NOK,∠NMK=12∠NOK,∠MNK=12∠MOK,
∴ ∠PMK=∠NMK=∠PNK=∠MNK,
∴ 点K是△PMN的三个角的角平分线的交点,
第21页 共24页 ◎ 第22页 共24页
二、填空题
【答案】
−2
【考点】
立方根的实际应用
立方根的性质
【解析】
利用立方根的定义即可求解.
【解答】
解:∵ (−2)3=−8,
∴ −8的立方根是−2.
故答案为:−2.
【答案】
−8x6y3
【考点】
分式的乘除运算
【解析】
直接利用积的乘方运算法则计算得出答案.
【解答】
(−2x2y)3=−8x6y3.
【答案】
a(a+b)(a−b)
【考点】
提公因式法与公式法的综合运用
【解析】
观察原式a3−ab2,找到公因式a,提出公因式后发现a2−b2是平方差公式,利用平方差公式继续分解可得.
【解答】
a3−ab2=a(a2−b2)=a(a+b)(a−b).
【答案】
π−2
【考点】
扇形面积的计算
【解析】
根据∠AOB=90∘,OA=OB可知△OAB是等腰直角三角形,根据S阴影=S扇形OAB−S△OAB即可得出结论.
【解答】
∵ ∠AOB=90∘,OA=OB,
∴ △OAB是等腰直角三角形.
∵ OA=2,
∴ S阴影=S扇形OAB−S△OAB=90π*22360−12×2×2=π−2.
【答案】
2
【考点】
函数的综合性问题
【解析】
本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.
【解答】
此题暂无解答
【答案】
−3
【考点】
根与系数的关系
【解析】
根据根与系数的关系结合x1+x2=1,可求出m的值,再将其代入x1x2=−3m中即可求出结论.
【解答】
∵ 方程x2−mx−3m=0的两根是x1、x2,
∴ x1+x2=m,x1x2=−3m,
又∵ x1+x2=1,
∴ m=1,
∴ x1x2=−3m=−3.
【答案】
M
【考点】
正方形的性质
旋转的性质
【解析】
根据以M为旋转中心,把正方形ABCD顺时针旋转90∘解答即可.
【解答】
若以M为旋转中心,把正方形ABCD顺时针旋转90∘,A点对应点为H,B点对应点为E,C点对应点为F,D点对应点为G,则可得到正方形EFGH.
【答案】
3π2
【考点】
切线的性质
弧长的计算
平行线的性质
【解析】
连接AE,根据圆的切线的性质可得AE⊥BC,解Rt△AEB可求出∠ABE,进而得到∠DAB,然后运用弧长公式就可求出DF的长度.
【解答】
连接AE,如图,
∵ AD为半径的圆与BC相切于点E,
∴ AE⊥BC,AE=AD=2.
在Rt△AEB中,
sin∠ABE=AEAB=222=22,
∴ ∠ABE=45∘.
∵ AD // BC,
∴ ∠DAB+∠ABE=180∘,
第21页 共24页 ◎ 第22页 共24页
∴ ∠DAB=135∘,
∴ DF的长度为135π×2180=3π2;
【答案】
(9625, 7225)
【考点】
坐标与图形变化-对称
【解析】
由直线的解析式求得A、B的坐标,设O1O与直线y=−43x+4的交点为D,作O1E⊥x轴于E,根据题意OO1⊥AB,根据三角形面积公式求得OD的长,即可求得OO1的长,然后通过三角形相似求得OE的长,进一步根据勾股定理求得O1E的长,即可求得对称点O1的坐标.
【解答】
如图,∵ 原点O关于直线y=−43x+4对称点O1,
∴ OO1⊥AB,
设O1O与直线y=−43x+4的交点为D,作O1E⊥x轴于E,
由直线y=−43x+4可知A(3, 0),B(0, 4),
∴ OA=3,OB=4,
∴ AB=5,
∵ S△AOB=12OA⋅OB=12AB⋅OD,
∴ OD=OA⋅OBAB=125,
∴ OO1=245,
∵ ∠ADO=∠O1EO=90∘,∠AOD=∠EOO1,
∴ △AOD∽△O1OE,
∴ OO1OA=OEOD,即2453=OE125,
∴ OE=9625,
∴ O1E=O1O2−OE2=7225,
∴ 点O1的坐标是(9625, 7225),
【答案】
5
【考点】
切线的性质
【解析】
首先说明点C、B在以OP为直径的圆上,根据直径是圆中最长的弦,即可解决问题.
【解答】
∵ PC、PB是⊙O的切线,
∴ ∠PCO=∠PBO=90∘,
∴ 点C、B在以OP为直径的圆上,
∵ BC是这个圆的弦,
∴ 当BC=OP=5时,BC的值最大(直径是圆中最长的弦).
三、解答题
【答案】
原式=(x+1)(x−1)(x−1)2+x(x−2)x−2⋅1x=x+1x−1+1=2xx−1,
当x=3时,原式=43−163−1=3.
【考点】
分式的化简求值
【解析】
原式第二项利用除法法则变形,约分后两项通分并利用同分母分式的加法法则计算得到最简结果,将x的值代入计算即可求出值.
【解答】
原式=(x+1)(x−1)(x−1)2+x(x−2)x−2⋅1x=x+1x−1+1=2xx−1,
当x=3时,原式=43−163−1=3.
【答案】
∵ 2x−3(x−1)≤6,
∴ 2x−3x+3≤6,
解得x≥−3,
这个不等式的解集在数轴上表示如下:
.
−4
查看更多