2017-2018学年江苏省南通市海安县九年级数学上期中试题含答案

2017-2018学年江苏省南通市海安县九年级数学上期中试题含答案

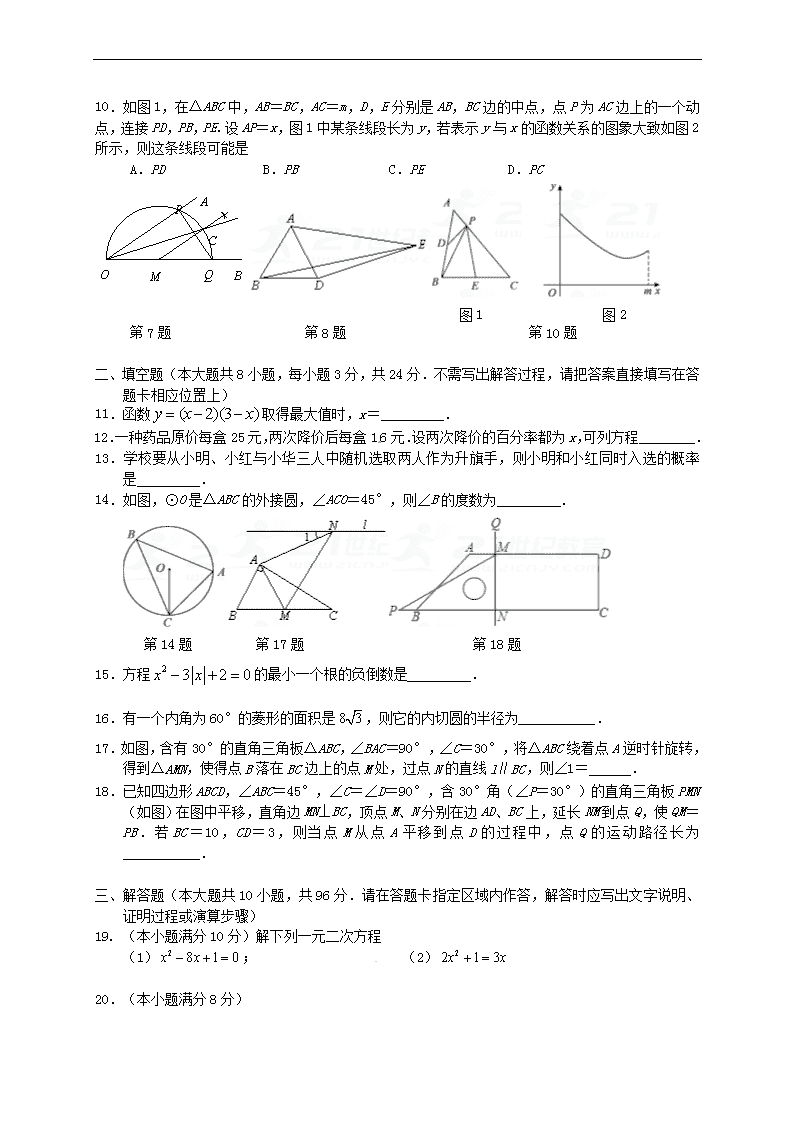
江苏省南通市海安县2018届九年级数学上学期期中试题 ‎ 一、选择题（本大题共10小题，每小题3分，共30分．在每小题给出的四个选项中，恰有一项是符合题目要求的，请将正确选项的字母代号填涂在答题卡相应位置上）‎ ‎1. 顺次连接正六边形的三个不相邻的顶点．得到如图所示的图形，该图形 A．既是轴对称图形也是中心对称图形 B．是轴对称图形但并不是中心对称图形 C．是中心对称图形但并不是轴对称图形 D．既不是轴对称图形也不是中心对称图形 ‎ 第1题 第3题 第5题 ‎2． 事件A：射击运动员射击一次，刚好射中靶心；事件B：连续掷两次硬币，都是正面朝上，则 A．事件A和事件B都是必然事件 B．事件A是随机事件，事件B是不可能事件 C．事件A是必然事件，事件B是随机事件 D．事件A和事件B都是随机事件 ‎3． 将如图所示的抛物线向右平移1个单位长度，再向上平移3个单位长度后，得到的抛物线解析式是 ‎ A．y＝(x－1)2＋1 B．y＝(x＋1)2＋1 C．y＝2(x－1)2＋1 D．y＝2(x＋1)2＋1 ‎ ‎4． 若方程(x－5)2＝19的两根为a和b，且a＞b，则下列结论中正确的是 ‎ A．a是19的算术平方根 B．是19的平方根 ‎ C．a－5是19的算术平方根 D．b＋5是19的平方根 ‎5． 如图，两个转盘分别自由转动一次，当停止转动时，两个转盘的指针都指向2的概率为 A． B． C． D．‎ ‎6．圆心角等于30°，半径等于6的弧的长度等于 A．π B．2π C．π D. 3π ‎7． 已知∠AOB，作图：‎ ‎ 步骤1：在OB上任取一点M，以点M为圆心，MO长为半径画半圆，分别交OA，OB于点P，Q．‎ ‎ 步骤2：过点M作PQ的垂线交于点C．‎ ‎ 步骤3：画射线OC．[来源:学科网ZXXK]‎ 则下列判断：①；②MC∥OA；③OP＝PQ；④OC平分∠AOB．其中正确的个数为 A．1 B．2 C．3 D．4‎ ‎8． 如图，△ABD是等边三角形，以AD为边向外作△ADE，使∠AED＝30°，且AE＝3，DE＝2，连接BE，则BE的长为 A．4 B． C．5 D． ‎ ‎9． 已知二次函数y＝x2－2mx（m为常数），当－1≤x≤2时，函数值y的最小值为－2，则m的值是2·1·c·n·j·y A． B． C． 或 D．或 ‎10．如图1，在△ABC中，AB＝BC，AC＝m，D，E分别是AB，BC边的中点，点P为AC边上的一个动点，连接PD，PB，PE.设AP＝x，图1中某条线段长为y，若表示y与x的函数关系的图象大致如图2所示，则这条线段可能是 A．PD B．PB C．PE D．PC2‎ O M Q B P C A ‎ ‎ ‎ 图1 图2‎ ‎ 第7题 第8题 第10题 二、填空题（本大题共8小题，每小题3分，共24分．不需写出解答过程，请把答案直接填写在答题卡相应位置上）www-2-1-cnjy-com ‎11．函数取得最大值时，x＝ ．‎ ‎12．一种药品原价每盒25元，两次降价后每盒16元．设两次降价的百分率都为x，可列方程________．‎ ‎13．学校要从小明、小红与小华三人中随机选取两人作为升旗手，则小明和小红同时入选的概率是 ．21*cnjy*com ‎14．如图，⊙O是△ABC的外接圆，∠ACO＝45°，则∠B的度数为 ．‎ ‎[来源:学科网ZXXK]‎ ‎ 第14题 第17题 第18题21教育网 ‎15．方程的最小一个根的负倒数是 ．‎ ‎16．有一个内角为60°的菱形的面积是，则它的内切圆的半径为___________．‎ ‎17．如图，含有30°的直角三角板△ABC，∠BAC＝90°，∠C＝30°，将△ABC绕着点A逆时针旋转，得到△AMN，使得点B落在BC边上的点M处，过点N的直线l∥BC，则∠1＝ ．‎ ‎18．已知四边形ABCD，∠ABC＝45°，∠C＝∠D＝90°，含30°角（∠P＝30°）的直角三角板PMN（如图）在图中平移，直角边MN⊥BC，顶点M、N分别在边AD、BC上，延长NM到点Q，使QM＝PB．若BC＝10，CD＝3，则当点M从点A平移到点D的过程中，点Q的运动路径长为___________．‎ 三、解答题（本大题共10小题，共96分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）‎ ‎19. （本小题满分10分）解下列一元二次方程 ‎（1）； （2） ‎ ‎20．（本小题满分8分）‎ 关于x的方程x2－(2k－1)x＋k2－2k＋3＝0有两个不相等的实数根．‎ ‎（1）求实数k的取值范围；‎ ‎（2）设方程的两个实数根分别为x1，x2，存不存在这样的实数k，使得|x1|－|x2|＝？若存在，求出这样的k值；若不存在，说明理由．‎ ‎21．（本小题满分9分）‎ 如图，把一个直角三角形ACB绕着30°角的顶点B顺时针旋转，使得得点A与CB的延长线上的点E重合．‎ ‎（1）三角尺旋转了多少度？‎ ‎（2）连接CD，试判断△CBD的形状；‎ ‎（3）求∠BDC的度数．‎ ‎22．（本小题满分7分）‎ 全面两孩政策实施后，甲，乙两个家庭有了各自的规划．假定生男生女的概率相同：‎ ‎（1）甲家庭已有一个男孩，准备再生一个孩子，则第二个孩子是男孩的概率是_________；‎ ‎（2）乙家庭没有孩子，准备生两个孩子，求至少有一个孩子是女孩的概率． ‎ ‎23．（本小题满分7分）‎ 如图是抛物线拱桥，已知水位在AB位置时，水面宽m，水位上升3m，达到警戒线CD，这时水面宽4m．若洪水到来时，水位以每小时0.25m的速度上升，求水过警戒线后几小时淹到拱桥顶？‎ ‎24．（本小题满分9分）‎ 某超市销售一种牛奶，进价为每箱24元，规定售价不低于进价．现在的售价为每箱36元，每月可销售60箱．市场调查发现：若这种牛奶的售价每降价1元，则每月的销量将增加10箱，设每箱牛奶降价x元(x为正整数)，每月的销量为y箱．[来源:学科网]‎ ‎ （1）写出y与x中间的函数关系式和自变量的取值范围；‎ ‎ （2）超市如何定价，才能使每月销售牛奶的利润最大？最大利润是多少元？‎ ‎25．（本小题满分10分）[来源:Zxxk.Com]‎ 如图，在⊙O中，半径OA⊥OB，过OA的中点C作FD∥OB交⊙O于D、F两点，且CD＝，以O为圆心，OC为半径作，交OB于E点．‎ ‎（1）求⊙O的半径OA的长；‎ ‎（2）计算阴影部分的面积．‎ ‎26．（本小题满分10分）‎ 如图，在Rt△ABC中，∠ACB＝90°，∠A＝30°，点D在AB上，以BD为直径的⊙O切AC于点E，连接DE并延长，交BC的延长线于点F．【版权所有：21教育】‎ ‎（1）求证：△BDF是等边三角形；‎ ‎（2）连接AF、DC，若BC＝3，写出求四边形AFCD面积的思路．‎ ‎27．（本小题满分13分）‎ ‎ 如图，四边形ABCD为一个矩形纸片，AB＝3，BC＝2，动点P自D点出发沿DC方向运动至C点后停止．△ADP以直线AP为轴翻折，点D落到点D1的位置．设DP＝x，△AD1P与原纸片重叠部分的面积为y．‎ ‎（1）当x为何值时，直线AD1过点C？‎ ‎（2）当x为何值时，直线AD1过BC的中点E？‎ ‎（3）求出y与x的函数关系式.‎ ‎28．（本小题满分13分）‎ 在平面直角坐标系xOy中，定义直线y＝ax＋b为抛物线y＝ax2＋bx的特征直线，C（a，b）为其特征点．设抛物线y＝ax2＋bx与其特征直线交于A、B两点（点A在点B的左侧）．‎ ‎（1）若特征点的坐标为为（1，3），则点A的坐标为______________．‎ ‎（2）当a＝1时，若△ABC是直角三角形，求b的值．‎ ‎（3）若a、b＞0，当点C在直线y＝ax＋b上，且△ABC的面积为2时，求a、b的值．‎ 八校联考九年级期中测试卷 数学参考答案 一、选择题 ‎1．B 2．D 3．C 4．C 5．D ‎6．A 7．C 8．B 9．D 10．C 二、填空题（本大题共8小题，每小题3分，共24分．）‎ ‎11．； 12．25(1－x)²＝16； 13．； 14．45°；‎ ‎15．； 16．； 17．30°； 18．7．‎ 三、解答题（本大题共10小题，共96分．）‎ ‎19. （1）x1＝4＋，x2＝4－；‎ ‎（2）x1＝1，x2＝．‎ ‎（过程4分，结果1分）‎ ‎20．解：（1）根据题意，得＞0．‎ ‎∴＞0．‎ 解得＞，即实数k的取值范围是k＞． 4分[来源:学。科。网]‎ ‎（2）由根与系数关系，得＝，＝．‎ ‎∵＝＞0，即＞0，∴、同号．‎ ‎∵＝，＞，∴＞0．∴＞0，＞0．‎ ‎∵＝，∴＝．‎ ‎∴＝5，即＝5．‎ ‎∴＝5．解得＝4．‎ ‎∵4＞，∴的值为4． 8分 ‎21．解：（1）由旋转的性质知旋转角度是∠ABE度数，△ACB≌△EDC，‎ ‎∴∠ABE＝180°－30°＝150° 3分 ‎（2）由△ACB≌△EDB知，BC＝BD，‎ ‎∴△CBD是等腰三角形． 6分 ‎（3）∵BC＝BD，∴∠BCD＝∠BDC，∴∠BDC＝∠EBD＝15°． 9分 ‎22．解：（1）； 3分 ‎（2）乙家庭没有孩子，准备生两个孩子所有可能出现得结果有（男，男），（男，女），（女，男），（女，女），一共有4种结果，它们出现得可能性相同，所有结果种，满足“至少有一个是女孩”的结果有三种，所以至少有一个孩子是女孩的概率是． 7分 ‎23．解：根据题意设抛物线解析式为：y＝ax2＋h 又∵B（2，0），D（2，3）‎ ‎∴解得：‎ ‎∴y＝－x2＋6 3分 ‎∴E（0，6）即OE＝6m ‎∴EF＝OE－OF＝3，‎ 则t＝＝＝12（小时）．‎ 答：水过警戒线后12小时淹到拱桥顶． 7分 ‎24．解：（1）y＝60＋10x，因为x≤36－24＝12，所以x为x≤12的正整数． 5分 ‎（2）w＝(36－x－24)(60＋10x)＝－10x2＋60x＋720＝－10(x－3)2＋810‎ 所以当超市降价3元时，即每箱33元时，所获利润最大，最大利润为810元． 9分 ‎25．解：（1）连接OD，‎ ‎∵FD∥OB，OA⊥OB，∴OA⊥FD.‎ ‎∵C为OA的中点，∴OC＝OA＝OD.‎ 设半径OA＝x，则OD＝x，OC＝‎ 在Rt△OCD中，OC2+CD2＝OD2，即，解得：x＝2（x＝－2舍去）‎ 所以，⊙O的半径OA的长为2． 5分 ‎（2）在Rt△COD中，∴∠COD＝60°.‎ 由题意可知：‎ S阴影＝S扇形AOB－S扇形COE－(S扇形AOD－S△COD)＝‎ ‎ ＝＝＝‎ 所以，阴影部分的面积为. 10分 ‎26．（1）证明：连接OE．‎ ‎ ∵AC切⊙O于点E，‎ ‎ ∴∠OEA＝90°．‎ ‎∵∠A＝30°，∠ACB＝90°,‎ ‎∴∠AOE＝60°，∠B＝60° .‎ ‎∵OD＝OE，‎ ‎ ∴∠ODE＝∠OED＝60°．‎ ‎ ∴∠F＝∠B＝∠ODE．‎ ‎∴△BDF是等边三角形． 6分 ‎ （2）解：如图，作DH⊥AC于点H.‎ ‎①由∠ACB＝90°，∠BAC＝30°，BC＝3，可求AB，AC的长；‎ ‎②由∠AEO＝90°，∠OAE＝30°，可知AO＝2OE，‎ 可求AD，DB，DH的长； ‎ ‎ ③由（1）可知BF＝BD，可求CF的长；‎ ‎ ④由AC，DH，CF的长可求四边形AFCD的面积. 10分 ‎27．解：（1）如图1，由题意得，△ADP≌△AD1P. ‎ ‎∴AD1＝AD＝2，PD＝PD1＝x, ∠PDA＝∠PD1A ＝90º.‎ ‎∵直线过点C，∴PD1⊥AC.‎ 在Rt△ABC中，‎ ‎∵AB＝3，BC＝2，∴AC＝＝,CD1＝－2．‎ 在Rt△PCD1中，PC2＝CD12＋CD12，即，解得x＝ ，‎ ‎∴当x＝时，直线AD1过点C． 4分 ‎（2）如图2，连接PE．‎ ‎∵E为BC中点，∴BE＝CE＝1．‎ 在Rt△ABE中，AE＝＝，‎ ‎∵AD1＝AD＝2，PD＝PD1＝x，∴D1E＝－2，PC＝3－x ．‎ 在Rt△PD1E 和Rt△PCE中，‎ ‎∴x2＋(－2)2＝(3－x)2＋12 ，解得x＝．‎ ‎∴当x＝时，直线AD1 过BC的中点E． 8分 ‎（3）如图3，当0＜x≤2时，y＝x．‎ 如图4，当2＜x≤3时，点D1在矩形外部，PD1与AB交于点F．‎ ‎∵AB∥CD，∴∠1＝∠2，∵∠1＝∠3，∴∠2＝∠3，∴FP＝FA．‎ 作PG⊥AB，垂足为点G，‎ 设FP＝FA＝a，‎ 由题意得，AG＝DP＝x，FG＝x－a．‎ 在Rt△PFG中，由勾股定理，得(x－a)2＋22＝a2解得a＝ ，‎ ‎∴y＝×2×＝ ，‎ 综上所述，当0＜x≤2时，y＝x；当2＜x≤3时，y＝． 13分 ‎28．（1）(－3，0) 3分 ‎（2）当a＝1时，A、B的坐标为(－b，0)和(1，1＋b)，C(1，b)．‎ ‎ 可见(1，1＋b)，(1，b)所连线段平行于y轴，‎ ‎ 当(1，1＋b)，C(1，b)其中一个点在x轴上时，△ABC是直角三角形，解得b＝0或b＝－1（舍去）．‎ ‎ 当(－b，0)是直角顶点的时候，利用勾股定理，可得b＝－1（舍去）或－． ‎ ‎ ∴a的值为0或－． 8分 ‎（3）∵当点C在直线y＝ax＋ab上，∴b＝a2＋ab．‎ ‎ ∵S△ABC＝a2＋ab，∴b＝2．‎ ‎ ∴a＝． 13分