- 2021-11-10 发布 |
- 37.5 KB |
- 10页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
上海市宝山区、嘉定区2012年中考二模(期中)数学试题
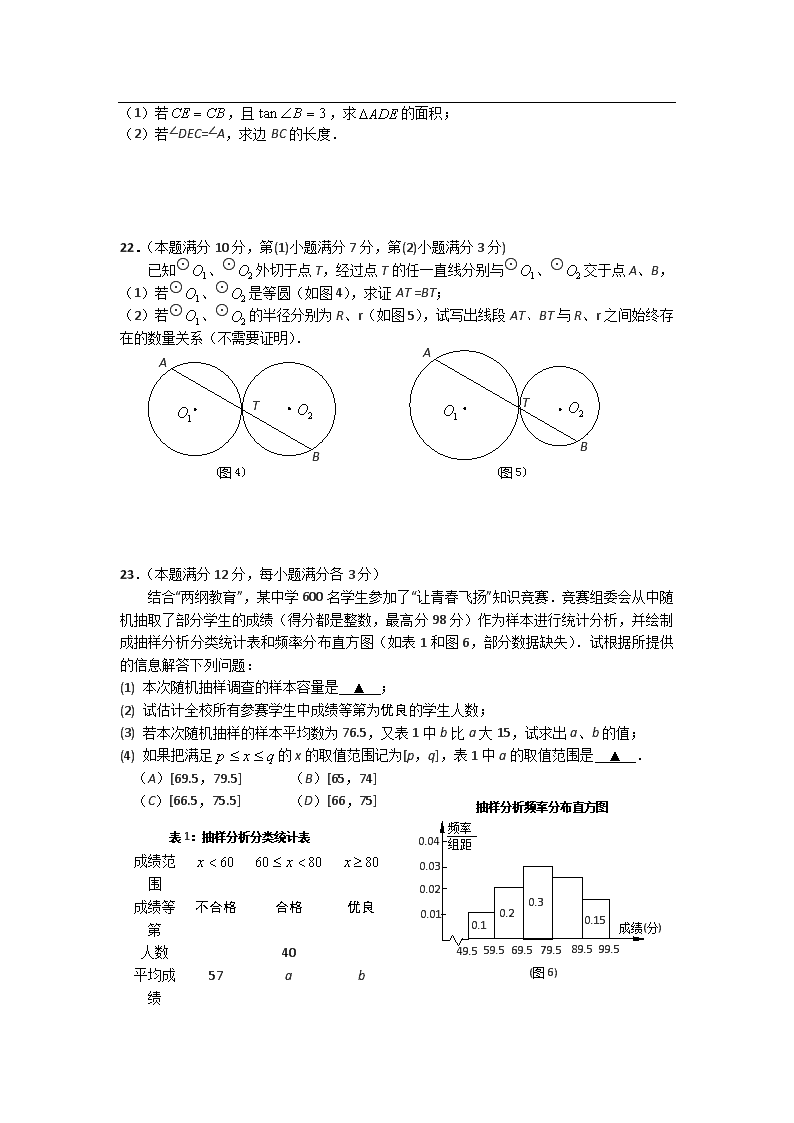
上海市宝山区(嘉定区)2012年中考二模 数学 (满分150分,考试时间100分钟) 考生注意: 1.本试卷含三个大题,共25题; 2.答题时,考生务必按答题要求在答题纸规定的位置上作答,在草稿纸、本试卷上答题一律无效; 3.除第一、二大题外,其余各题如无特别说明,都必须在答题纸的相应位置上写出证明或计算的主要步骤. 一、选择题:(本大题共6题,每题4分,满分24分) 【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答题纸的相应位置上】 1.下列计算正确的是 ( ▲ ). (A); (B); (C); (D). 2.如果,,那么下列不等式成立的是( ▲ ). (A) ; (B) ; (C) ; (D) . 3.一次函数的图像不经过( ▲ ). (A)第一象限; (B)第二象限; (C)第三象限; (D)第四象限. 4.在研究反比例函数图像与性质时,由于计算粗心,小明误认为(,)、(,)、(,)、(,)、(,)五个点在同一个反比例函数的图像上,后来经检查发现其中有一个点不在,这个点是( ▲ ). (A)(,); (B) (,); (C)(,); (D) (,). ① x y O 1 1 ③ ② ④ (图1) 5.如图1,在编号为①、②、③、④的四个三角形中,关于x轴对称的两个三角形是( ▲ ). (A)①和②; (B)②和③; (C)①和③; (D)②和④. 6.下列命题中,假命题是( ▲ ). (A)如果一个点到圆心的距离大于这个圆的半径, 那么这个点在圆外; (B)如果一个圆的圆心到一条直线的距离小于它 的半径,那么这条直线与这个圆有两个交点; (C)边数相同的正多边形都是相似图形; (D)正多边形既是轴对称图形,又是中心对称图形. 二、填空题:(本大题共12题,每题4分,满分48分) 【请将结果直接填入答题纸的相应位置】 7.计算: ▲ . 8.计算: ▲ . 9.如果关于的方程(为常数)有两个相等的实数根,则 ▲ . 10.已知函数,若,则= ▲ . 11.已知一个二次函数的图像在y轴左侧部分是上升的,在y轴右侧部分是下降的,又经过点A(1,1).那么这个二次函数的解析式可以是 ▲ (写出符合要求的一个解析式即可). 12.在一个不透明的袋子中装有2个白球,个红球,它们除了颜色不同外,其余均相同. 若从中随机摸出一个球,摸到红球的概率是,则的值等于 ▲ . 13.半径为2的圆中,60°的圆心角所对的弦长为 ▲ . 14.在△ABC中,点D、E分别在边AB和AC上,且DE∥BC,如果AD=5,DB=10,那么:的值为 ▲ . 15.已知△ABC中,∠A=90°,∠B=θ,AC=b,则AB= ▲ (用b和θ的三角比表示). 16.已知G是△ABC的重心,设,,那么= ▲ (用、表示). (图2) x y O C B A 17.已知⊙O1与⊙O2相切,⊙O1的半径比⊙O2的2倍还大1, 又O1O2=7,那么⊙O2的半径长为 ▲ . 18.如图2,在平面直角坐标系中,点A在x轴上,点B的坐标 为(4,2),若四边形为菱形,则点的坐标为 ▲ . 三、解答题:(本大题共7题,满分78分) 19.(本题满分10分)计算:. 20.(本题满分10分)解方程组: (图3) 21.(本题满分10分,每小题满分各5分) 如图3,已知梯形中,AB∥CD,AB=13,CD=4, 点在边AB上,DE∥. (1)若,且,求的面积; (2)若∠DEC=∠A,求边BC的长度. 22.(本题满分10分,第(1)小题满分7分,第(2)小题满分3分) 已知⊙、⊙外切于点T,经过点T的任一直线分别与⊙、⊙交于点A、B, (1)若⊙、⊙是等圆(如图4),求证AT =BT; (图5) T B A (图4) T B A (2)若⊙、⊙的半径分别为R、r(如图5),试写出线段AT、BT与R、r之间始终存在的数量关系(不需要证明). 23.(本题满分12分,每小题满分各3分) 结合“两纲教育”,某中学600名学生参加了“让青春飞扬”知识竞赛.竞赛组委会从中随机抽取了部分学生的成绩(得分都是整数,最高分98分)作为样本进行统计分析,并绘制成抽样分析分类统计表和频率分布直方图(如表1和图6,部分数据缺失).试根据所提供的信息解答下列问题: (1) 本次随机抽样调查的样本容量是 ▲ ; (2) 试估计全校所有参赛学生中成绩等第为优良的学生人数; (3) 若本次随机抽样的样本平均数为76.5,又表1中b比a大15,试求出a、b的值; (4) 如果把满足的x的取值范围记为[p,q],表1中a的取值范围是 ▲ . (A)[69.5,79.5] (B)[65,74] 抽样分析频率分布直方图 (图6) 成绩(分) 0.01 0.04 0.02 0.03 49.5 0.1 0.2 0.3 0.15 59.5 69.5 79.5 89.5 99.5 (C)[66.5,75.5] (D)[66,75] 表1:抽样分析分类统计表 成绩范围 成绩等第 不合格 合格 优良 人数 40 平均成绩 57 a b 24.(本题满分12分,每小题满分各4分) 如图7,平面直角坐标系中,已知点A(2,3),线段垂直于轴,垂足为,将线段绕点A逆时针方向旋转90°,点B落在点处,直线与轴的交于点. (图7) 1 1 x y A O (1)试求出点D的坐标; (2)试求经过、、三点的抛物线的表达式, 并写出其顶点E的坐标; (3)在(2)中所求抛物线的对称轴上找点,使得 以点、、为顶点的三角形与△ACD相似. 25.(本题满分14分,第(1) 、(2)小题满分各5分,第(3)小题满分4分) 已知△ABC中,(如图8),点到两边的距离相等,且PA=PB. (1)先用尺规作出符合要求的点P(保留作图痕迹,不需要写作法),然后判断△ABP的形状,并说明理由; (2)设,,试用、的代数式表示的周长和面积; (3)设CP与AB交于点D,试探索当边AC、BC的长度变化时,的值是否发生变化,若不变,试求出这个不变的值,若变化,试说明理由. A B C (备用图) A B C (图 ) 8 2011学年第二学期期中考试九年级 数学参考答案 一、选择题:(本大题共6题,每题4分,满分24分) 1、C; 2、A; 3、B; 4、C; 5、B; 6、D. 二、填空题:(本大题共12题,每题4分,满分48分) 7、; 8、; 9、; 10、; 11、【答案不唯一,如等】; 12、; 13、; 14、; 15、【答案不唯一,等等价形式均可】; 16、; 17、2或6; 18、(,). 三、解答题:(本大题共7题,满分78分) 19.解: ………………………………5分 ………………………………2分 ………………………………3分 20.解:方程可变形为 . 得或. ………………………1分 方程可变形为 . 两边开平方,得 或 . ……………………1分 因此,原方程组可化为四个二元一次方程组: …………………4分 分别解这四个方程组,得原方程组的解是 ………………4分 21.解:(1)分别过点C、D作、,交于点、(如图3). (图3) G F ∵AB∥CD ∴. ………1分 ∵AB∥CD,DE∥, ∴. ∵AB=13,CD=4, ∴. ………1分 ∵,, ∴. ………1分 在Rt△BCF中,由,得 3,即,. ………1分 ∴. ∴. ………1分 (2)∵AB∥CD,∴. ………1分 又∵∠DEC=∠A, ∴△CDE∽△DEA. ………1分 ∴ . ………1分 ∵,CD=4,∴. ∴,(负值已舍). ………1分 ∵AB∥CD,DE∥, ∴. ………1分 22.(1)证明:联结. ∵⊙、⊙外切于点T,∴点T在上. …1分 过、分别作、,垂足为C、D(如图4), (图4) T B A C D ∴ ∥. …1分 ∴ . …1分 ∵⊙、⊙是等圆,∴. …1分 ∴,∴. …1分 在⊙中,∵,∴. 同理 . … 1分 ∴,即. … 1分 (2)解:线段AT、BT与R、r之间始终存在的数量关系是. … 3分 23.解:(1) 80 ; … 3分 (2) 成绩位于79.5~89.5的频率为 . … 1分 所以全校所有参赛学生中成绩等第为优良的学生人数为 (人) … 2分 (3) 本次随机抽样分析成绩不合格的人数为(人), 成绩优良的人数为(人), … 1分 依据题意,可得方程组 ……1分 解得 ……1分 (4) D . ……3分 24.(本题满分12分,每小题满分各4分) 解:(1)点C的坐标为(,). ……1分 (图7) 1 1 x y A O C D E F 设直线的表达式为. 易得 解得 ……2分 所以直线的表达式为. 当时,,. 所以点D的坐标为(,). ……1分 (2)设经过、、三点的抛物线的表达式 为() ……1分 易得 ……1分 解得 ……1分 因此,所求的抛物线的表达式为. 其顶点坐标为 (,). ……1分 (3)点F在的对称轴(即直线)上,所以设点F的坐标为(1,). 由题意可得 ,, ∴ , . 所以若以、、为顶点的三角形与△ACD相似,必有一个角的度数为, 由此可得点F必定在点E的上方, , ……1分 所以当或时, 以、、为顶点的三角形与△ACD相似. ……1分 由点D(,)、C(,)、A(2,3)、(,)易得 ,,. ∴ 或. 解得 或. 故符合题意的点F有两个,其坐标为(1,5)或(1,6). ……2分 25.(本题满分14分,第(1) 、(2)小题满分各5分,第(3)小题满分4分) 解:(1)依题意,点P既在的平分线上,又在线段AB的垂直平分线上. 如图8—1,作的平分线CP,作线段的垂直平分线PM,CP与PM的 交点即为所求的P点。【有作图痕迹,且作图基本正确】 ……2分. 是等腰直角三角形. ……1分(只写出等腰三角形,不得分). 理由如下:过点P分别作、,垂足为E、F(如图8—2). ∵平分,、,垂足为E、F, ∴. 又∵ ,∴ ≌. ∴ . ………1分 ∵,,, ∴, 从而. ………1分 M 图8-1 图8-2 又 ∴ 是等腰直角三角形. (2)如图8-2,在中,,,, ∴. ………1分 由≌,≌,可得,. ∴.………1分 在中,,,, ∴. ∴. 所以的周长为:. ………1分 因为的面积=的面积的面积的面积 == =(). ………2分 【或 .】 (3)【法1】过点分别作、,垂足为、(图8-3). 易得 . ……1分 由∥得 ①; 由∥得 ② ①+②,得 ,即 . ………2分 ∴ , 即 . ………1分 【法2】(前面同法1)又 ,. ∴ ∴. ……2分 图8—3 图8-4 ∴ ,即 . ……1分 【法3】过点作,垂足为(图8-4). 在中,, ……1分 由∥得 ①; ② ①+②,得 ,即 . ………2分 ∴ ,即 . ………1分 【法4】过点作∥,交射线于点(如图8-5) 易得 ,. ………1分 ∵∥,∴. ∴ ,. ………2分 即 . ………1分 【法5】过点作的平行线,交射线于点 (见图8-6), 得,,………1分 又 , 即 , ……2分 所以 , ………1分 【法6】分别过点、分别作的平行线,交射线于点,交射线于点(见图8-7). 得, ……1分 又 , ∴ ,………2分 图8-5 图8-6 图8-7 即,.………1分查看更多