- 2021-11-10 发布 |
- 37.5 KB |
- 4页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
苏教版数学九年级上册教案3-4方差
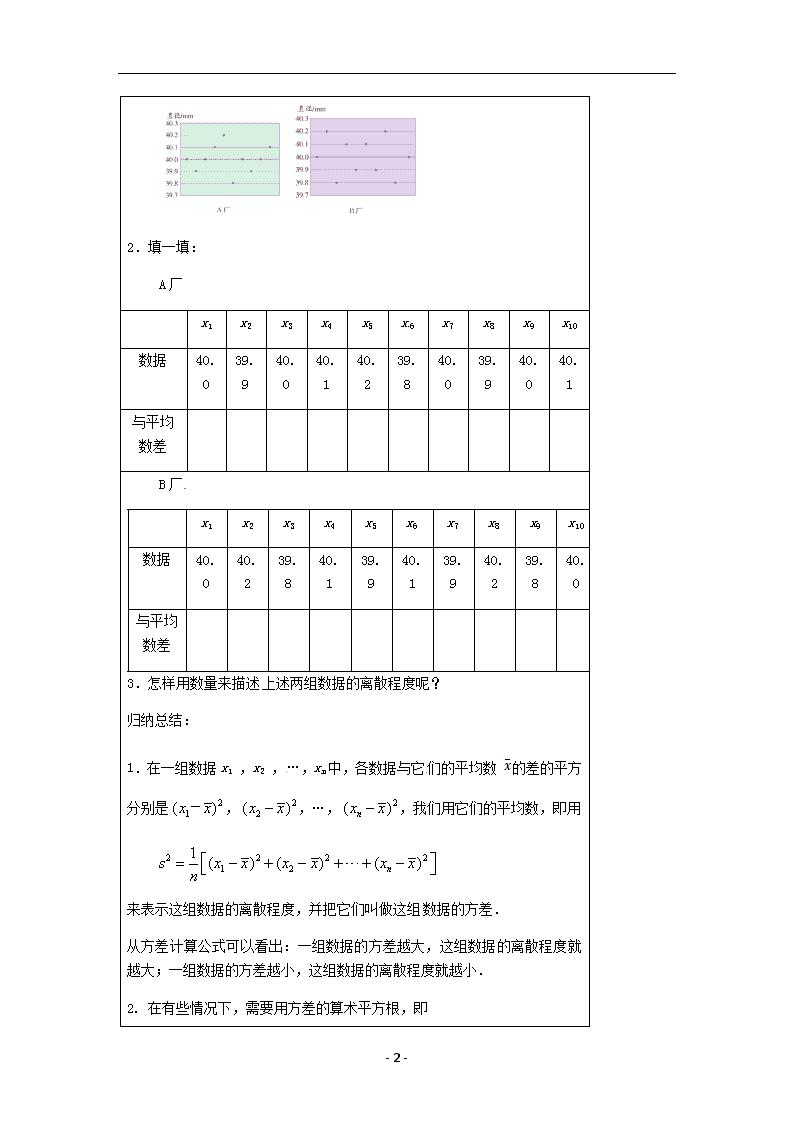
- 1 - 3.4 方差 教学目标 【知识与能力】 了解极差和方差是刻画数据离散程度的一个统计量,并在具体情境中加以应用. 【过程与方法】 掌握极差和方差概念,会计算极差和方差,并理解其统计意义. 【情感态度价值观】 经历刻画数据离散程度的探索过程,感受表示数据离散程度的必要性. 教学重难点 【教学重点】 理解极差和方差概念,并在具体情境中加以应用. 【教学难点】 应用极差和方差概念解释实际问题中数据的离散程度,并形成相应的数学经验. 课前准备 无 教学过程 情境创设: 2015 年世乒赛将在苏州举行,在使用乒乓球的大小时,其尺寸有严格的要 求,乒乓球的标准直径为 40mm.质检部门对 A、B 两厂生产的乒乓球的直径 进行检测,从 A、B 两厂生产的乒乓球中各抽取了 10 只,测量结果如下(单 位:mm): A 厂:40. 0,39.9,40.0,4 0.1,40.2,39.8,4 0.0,39.9,40.0, 40.1. B 厂:40.0,40.2,39.8,40.1,39.9,40.1,39.9,40.2,39.8,40.0. 1.你能从哪些角度认识这些数据? 极差的概念:一组数据中最大值与最小值的差,能反映这组数据的变 化范围,我们就把这样的差叫做极差,即极差=最大值-最小值. 通常,一组数据的极差越小,这组数据的波动幅度也越小. 2.通过计算发现,A、B 两厂生产的乒乓球的直径的平均数都是 40mm, 极差都是 0.4 mm.怎样更精确地比较这两组数据的离散程度呢? 探索活动: 1.将上面的两组数据绘制成下图: - 2 - 2.填一填: A 厂 x1 x2 x3 x4 x5 x 6 x7 x8 x9 x10 数据 40. 0 39. 9 40. 0 40. 1 40. 2 39. 8 40. 0 39. 9 40. 0 40. 1 与平均 数差 B 厂 x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 数据 40. 0 40. 2 39. 8 40. 1 39. 9 40. 1 39. 9 40. 2 39. 8 40. 0 与平均 数差 3.怎样用数量来描述上述两组数据的离散程度呢? 归纳总结: 1.在一组数据 x1 ,x2 ,…,xn 中,各数据与它们的平均数 _ x 的差的平方 分别是 2 1( )x x- , 2 2( )x x ,…, 2( )nx x ,我们用它们的平均数,即用 2 2 2 2 1 2 1 ( ) ( ) ( )ns x x x x x xn 来表示这组数据的离散程度,并把它们叫做这组数据的方差. 从方差计算公式可以看出:一组数据的方差越大,这组数据的离散程度就 越大;一组数据的方差越小,这组数据的离散程度就越小. - 3 - 2. 在有些情况下,需要用方差的算术平方根,即 2 2 2 1 2 1 ( ) ( ) ( )ns x x x x x xn 来描述一组数据的离散程度,并把它叫做这组数据的标准差. 例题精讲: 在一次芭蕾舞比赛中,甲、乙两个芭蕾舞团都表演了舞剧《天鹅湖》,参 加表演的女演员身高(单位:cm)如下表所示: 甲 163 164 164 165 165 166 166 167 乙 163 165 165 166 166 167 168 168 哪个芭蕾舞团女演员的身高更整齐? 巩固练习: 1.某地某日最高气温为 12℃,最低气温为-7℃,该日气温的极差是 . 2.一组数据 1,2,3,4,5 的平均数是 3,则方差是 . 一组数据 3,6,9,12,15 的方差是 . 一组数据 4,7,10,13,16 的方差是 ,标准差是 . 3.在某旅游景区上山的一条小路上,有一些断断续续的台阶.下图是其中 的甲、乙段台阶路的示意图(图中的数字表示每一级台阶的 高度).请你 回答下列问题(单位:cm): (1)哪段台阶路走起来更舒服?为什么? (2)为方便游客行走,需要重新整修上山的小路.对于这两段台阶路,在 台阶数不变的情况下,请你提出合理的整修建议. 4.请你列举出方差、标准差的生活实例,并说给你的同桌听一听. 16 14 14 16 15 15 甲路段 17 19 10 18 15 11 乙路段 - 4 - 总结提高: 谈谈你的收获.查看更多