2012年江苏省徐州市中考数学试题（含答案）

2012年江苏省徐州市中考数学试题（含答案）

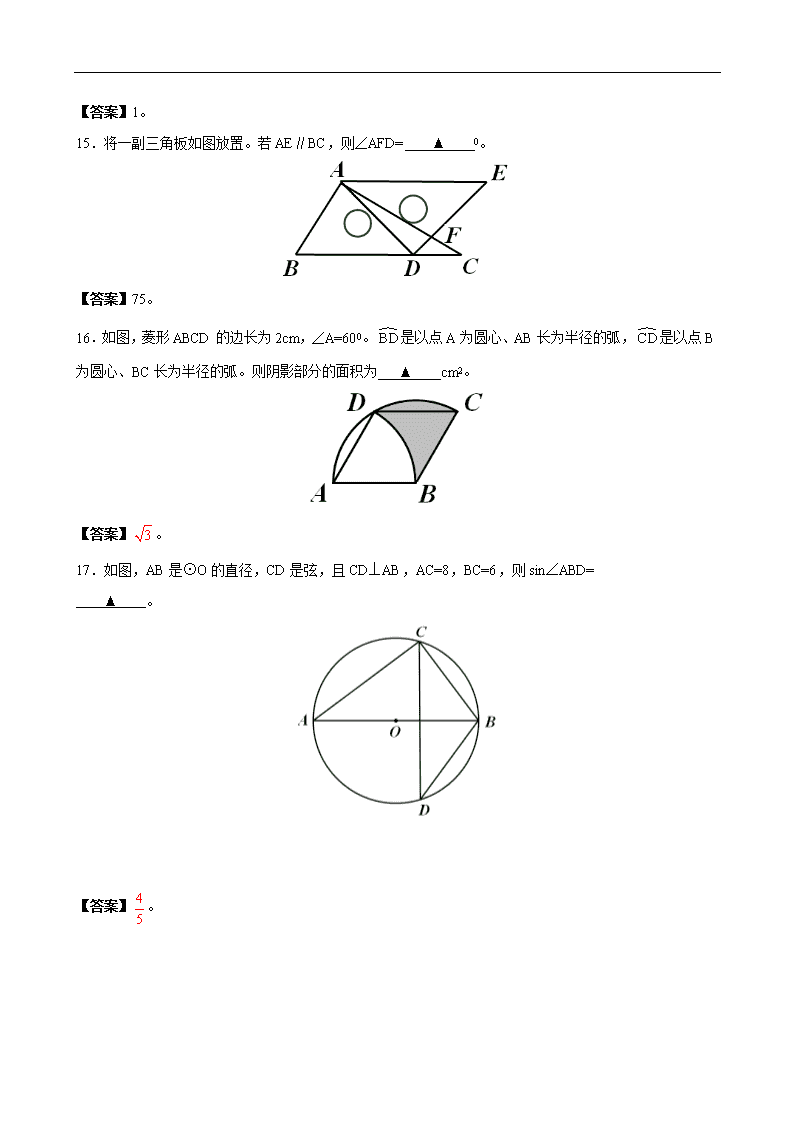
‎2012年中考数学试题（江苏徐州卷）‎ ‎（本试卷满分120分，考试时间120分钟）‎ 一、选择题(本大题共有8小题，每小题3分，共24分)‎ ‎1．－2的绝对值是【 】‎ A．－2 B． 2 C． D．－‎ ‎【答案】B。‎ ‎2．计算的结果是【 】‎ A． B． C． D．‎ ‎【答案】A。‎ ‎3． 2011年徐州市接待国内外旅游人数约为24 800 000人次，该数据用科学计数法表示为【 】‎ A． B． C． D．‎ ‎【答案】A。‎ ‎4．如果等腰三角形的两边长分别为2和5，则它的周长为【 】‎ A．9 B．7 C．12 D．9或12‎ ‎【答案】C。‎ ‎5．如图，A、B、C是⊙O上的点，若∠AOB=700，则∠ACB的度数为【 】[来源:Zxxk.Com]‎ A．700 B．500 C．400 D．350‎ ‎【答案】D。‎ ‎6．一次函数y=x－2的图象不经过【 】‎ A．第一象限 B．第二象限 C．第三象限 D．第一象限 ‎【答案】B。‎ ‎7．九（2）班“环保小组”的5位同学在一次活动中捡废弃塑料袋的个数分别为：4，6，8，16，16。这组数据的中位数、众数分别为【 】‎ A．16，16 B．10，16 C．8，8 D．8，16‎ ‎【答案】D。‎ ‎8．如图，在正方形ABCD中，E是CD的中点，点F在BC上，且FC=BC。图中相似三角形共有【 】‎ A．1对 B．2对 C．3对 D．4对 ‎【答案】C。‎ 二、选择题(本大题共有10小题，每小题2分，共20分)‎ ‎9．∠α=800，则α的补角为 ▲ 0。‎ ‎【答案】100。‎ ‎10．分解因式： ▲ 。‎ ‎【答案】。‎ ‎11．四边形内角和为 ▲ 0。‎ ‎【答案】360。‎ ‎12．下图是某地未来7日最高气温走势图，这组数据的极差为 ▲ 0C。‎ ‎【答案】7。‎ ‎13．正比例函数的图象与反比例函数的图象相交于点（1，2），则 ‎ ▲ 。‎ ‎【答案】4。‎ ‎14．若，则 ▲ 。‎ ‎【答案】1。‎ ‎15．将一副三角板如图放置。若AE∥BC，则∠AFD= ▲ 0。‎ ‎【答案】75。‎ ‎16．如图，菱形ABCD的边长为2cm，∠A=600。是以点A为圆心、AB长为半径的弧，是以点B为圆心、BC长为半径的弧。则阴影部分的面积为 ▲ cm2。‎ ‎【答案】。[来源:学|科|网Z|X|X|K]‎ ‎17．如图，AB是⊙O的直径，CD是弦，且CD⊥AB，AC=8，BC=6，则sin∠ABD=‎ ‎ ▲ 。‎ ‎【答案】。‎ ‎18．函数的图象如图所示，关于该函数，下列结论正确的是 ▲ （填序号）。‎ ①函数图象是轴对称图形；②函数图象是中心对称图形；③当x>0时，函数有最小值；④点（1，4）在函数图象上；⑤当x＜1或x＞3时，y＞4。‎ ‎【答案】②③④。‎ 三、解答题(本大题共有10小题，共76分)‎ ‎19． ‎ ‎（1）计算：；‎ ‎【答案】解：原式=。‎ ‎（2）解不等式组：。‎ ‎【答案】解：，‎ ‎ 由①得，x＜5；由②得，x＞3。‎ ‎ ∴不等式组的解为3＜x＜5。‎ ‎20．抛掷一枚均匀的硬币2次，请用列表或画树状图的方法抛掷的结果都是反面朝上的概率。‎ ‎【答案】解：画树状图如下：‎ ‎ ∵共有4种等可能，2次都是反面朝上只有1种结果，‎ ‎ ∴2次都是反面朝上的概率为。‎ ‎21． 2011年徐州市全年实现地区生产总值3551.65亿元，按可比价格计算，比上年增长13.5%，经济平稳较快增长。其中，第一产业、第二产业、第三产业增加值与增长率情况如图所示：‎ ‎ 根据图中信息，写成下列填空：‎ ‎ （1）第三产业的增加值为 ▲ 亿元：‎ ‎（2）第三产业的增长率是第一产业增长率的 ▲ 倍（精确到0.1）；‎ ‎（3）三个产业中第 ▲ 产业的增长最快。‎ ‎【答案】解：（1）1440.06。‎ ‎ （2）3.2。‎ ‎ （3）二。‎ ‎22．某校为了进一步开展“阳光体育”活动，计划用2000元购买乒乓球拍，用2800元购买羽毛球拍。已知一副羽毛球拍比一副乒乓球拍贵14元。该校购买的乒乓球拍与羽毛球拍的数量能相同吗？请说明理由。‎ ‎【答案】解：不能相同。理由如下：‎ 假设能相等，设兵乓球每一个x元，羽毛球就是x+14。‎ ‎∴得方程，解得x=35。‎ 但是当x=35时，2000÷35不是一个整数，这不符合实际情况，不可能球还能零点几个地买，所以不可能。‎ ‎23．如图，C为AB的中点。四边形ACDE为平行四边形，BE与CD相交于点F。‎ 求证：EF=BF。‎ ‎【答案】证明：∵四边形ACDE为平行四边形，∴ED=AC，ED∥AC。∴∠D=∠FCB，∠DEF=∠B。‎ ‎ 又∵C为AB的中点，∴AC=BC。∴ED=BC。‎ ‎ 在△DEF和△CBF中，∵∠D=∠FCB，ED=BC，∠DEF=∠B，‎ ‎ ∴△DEF≌△CBF（SAS）。∴EF=BF。‎ ‎24．二次函数的图象经过点（4，3），（3，0）。‎ ‎ （1）求b、c的值；‎ ‎ （2）求出该二次函数图象的顶点坐标和对称轴；‎ ‎ （3）在所给坐标系中画出二次函数的图象。‎ ‎【答案】解：（1）∵二次函数的图象经过点（4，3），（3，0），‎ ‎ ∴，解得。‎ ‎ （2）∵该二次函数为。‎ ‎ ∴该二次函数图象的顶点坐标为（2，－1），对称轴为x=1。‎ ‎ （3）列表如下：‎ x ‎···‎ ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎···‎ y ‎···‎ ‎3‎ ‎0‎ ‎1‎ ‎0[来源:Zxxk.Com]‎ ‎3‎ ‎···‎ ‎ 描点作图如下：‎ ‎25．为了倡导节能低碳的生活，某公司对集体宿舍用电收费作如下规定：一间宿舍一个月用电量不超过a千瓦时，则一个月的电费为20元；若超过a千瓦时，则除了交20元外，超过部分每千瓦时要交元。某宿舍3月份用电80千瓦时，交电费35元；4月份用电45千瓦时，交电费20元。‎ ‎（1）求a的值；‎ ‎（2）若该宿舍5月份交电费45元，那么该宿舍当月用电量为多少千瓦时？‎ ‎【答案】解：（1）根据3月份用电80千瓦时，交电费35元，得，‎ ‎ ，即。‎ ‎ 解得a=30或a=50。‎ ‎ 由4月份用电45千瓦时，交电费20元，得，a≥45。‎ ‎ ∴a=50。‎ ‎（2）设月用电量为x千瓦时，交电费y元。则 ‎ ‎ ‎ ∵5月份交电费45元，∴5月份用电量超过50千瓦时。‎ ‎∴45=20＋0.5（x－50），解得x=100。‎ ‎ 答：若该宿舍5月份交电费45元，那么该宿舍当月用电量为100千瓦时。‎ ‎26．如图，为测量学校围墙外直立电线杆AB的高度，小亮在操场上点C处直立高3m的竹竿CD，然后退到点E处，此时恰好看到竹竿顶端D与电线杆顶端B重合；小亮又在点C1处直立高3m的竹竿C1D1，然后退到点E1处，此时恰好看到竹竿顶端D1与电线杆顶端B重合。小亮的眼睛离地面高度EF=1.5m，量得CE=2m，EC1=6m，C1E1=3m。‎ ‎（1）△FDM∽△ ▲ ，△F1D1N∽△ ▲ ；‎ ‎（2）求电线杆AB的高度。‎ ‎【答案】解：（1）FBG，F1BG。‎ ‎（2）根据题意，∵D1C1∥BA，∴△F1D1N∽△F1BG。∴。‎ ‎ ∵DC∥BA，∴△FDNN∽△FBG。∴。‎ ‎ ∵D1N=DM，∴，即。∴GM=16。‎ ‎ ∵，∴。∴BG-13.5。‎ ‎ ∴AB=BG＋GA=15（m）。‎ ‎ 答：电线杆AB的高度为了15m。‎ ‎27．如图1，A、B、C、D为矩形的四个顶点，AD=4cm，AB=dcm。动点E、F分别从点D、B出发，点E以1 cm/s的速度沿边DA向点A移动，点F以1 cm/s的速度沿边BC向点C移动，点F移动到点C时，两点同时停止移动。以EF为边作正方形EFGH，点F出发xs时，正方形EFGH的面积为ycm2。已知y与x的函数图象是抛物线的一部分，如图2所示。请根据图中信息，解答下列问题：‎ ‎（1）自变量x的取值范围是 ▲ ；‎ ‎（2）d= ▲ ，m= ▲ ，n= ▲ ；‎ ‎（3）F出发多少秒时，正方形EFGH的面积为16cm2？‎ ‎【答案】解：（1）0≤x≤4。‎ ‎ （2）3，2，25．‎ ‎ （3）过点E作EI⊥BC垂足为点I。则四边形DEIC为矩形。‎ ‎ ∴EI=DC=3，CI=DE=x。‎ ‎ ∵BF=x，∴IF=4－2x。[来源:学§科§网Z§X§X§K]‎ ‎ 在Rt△EFI中，。‎ ‎ ∵y是以EF为边长的正方形EFGH的面积，‎ ‎ ∴。‎ ‎ 当y=16时，，‎ 解得，。‎ ‎∴F出发或秒时，正方形EFGH的面积为16cm2。‎ ‎28．如图，直线与x轴、y轴分别相交于点A、B，与正比例函数的图象相交于点C、D（点C在点D的左侧），⊙O是以CD长为半径的圆。CE∥x轴，DE∥y轴，CE、DE相交于点E。‎ ‎（1）△CDE是 ▲ 三角形；点C的坐标为 ▲ ，点D的坐标为 ▲ （用含有b的代数式表示）；‎ ‎（2）b为何值时，点E在⊙O上？‎ ‎（3）随着b取值逐渐增大，直线与⊙O有哪些位置关系？求出相应b的取值范围。‎ ‎【答案】解：（1）等腰直角；；。‎ ‎ （2）当点E在⊙O上时，如图，连接OE。则OE=CD。‎ ‎∵直线与x轴、y轴相交于点A（－b，0），B（0，b），CE∥x轴，DE∥y轴，‎ ‎ ∴△DCE、△BDO是等腰直角三角形。‎ ‎ ∵整个图形是轴对称图形，‎ ‎ ∴OE平分∠AOB，∠AOE=∠BOE=450。‎ ‎ ∵CE∥x轴，DE∥y轴，‎ ‎ ∴四边形CAOE、OEDB是等腰梯形。‎ ‎ ∴OE=AC=BD。‎ ‎ ∵OE=CD，∴OE=AC=BD=CD。‎ ‎ 过点C作CF⊥x轴，垂足为点F。‎ ‎ 则△AFC∽△AOB。∴。∴。‎ ‎ ‎ ‎ ∴，解得。‎ ‎ ∵，∴。‎ ‎ ∴当时，点E在⊙O上。‎ ‎（3）当⊙O与直线相切于点G时，‎ ‎ 如图 ，连接OG。‎ ‎ ∵整个图形是轴对称图形，‎ ‎ ∴点O、E、G在对称轴上。‎ ‎∴GC=GD=CD=OG=AG。∴AC=CG=GD=DB。∴AC=AB。‎ 过点C作CH⊥x轴，垂足为点H。 则△AHC∽△AOB。‎ ‎∴。∴。‎ ‎∴，解得。‎ ‎∵，∴。‎ ‎∴当时，直线与⊙O相切；‎ 当时，直线与⊙O相离；‎ 当时，直线与⊙O相交。‎