- 2021-11-10 发布 |
- 37.5 KB |
- 11页
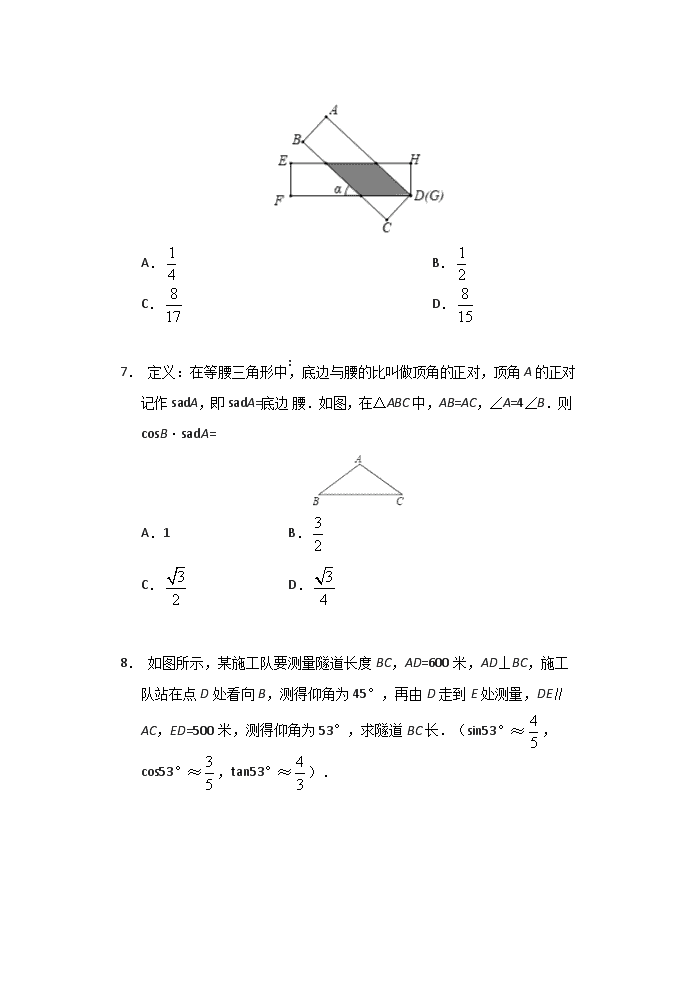
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2020中考数学三轮复习——锐角三角函数 练习
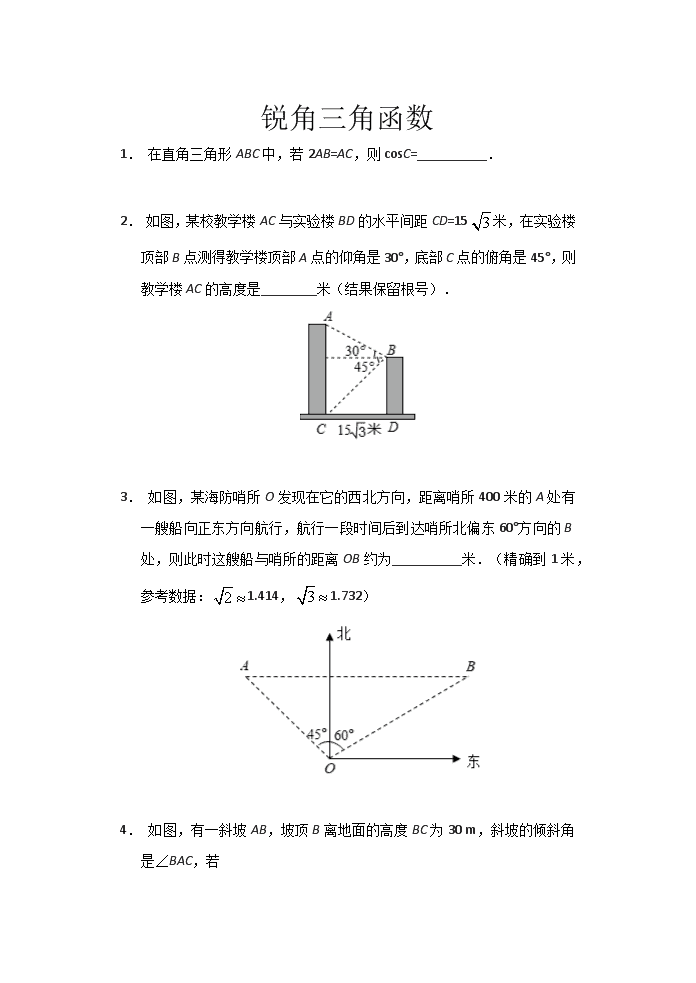
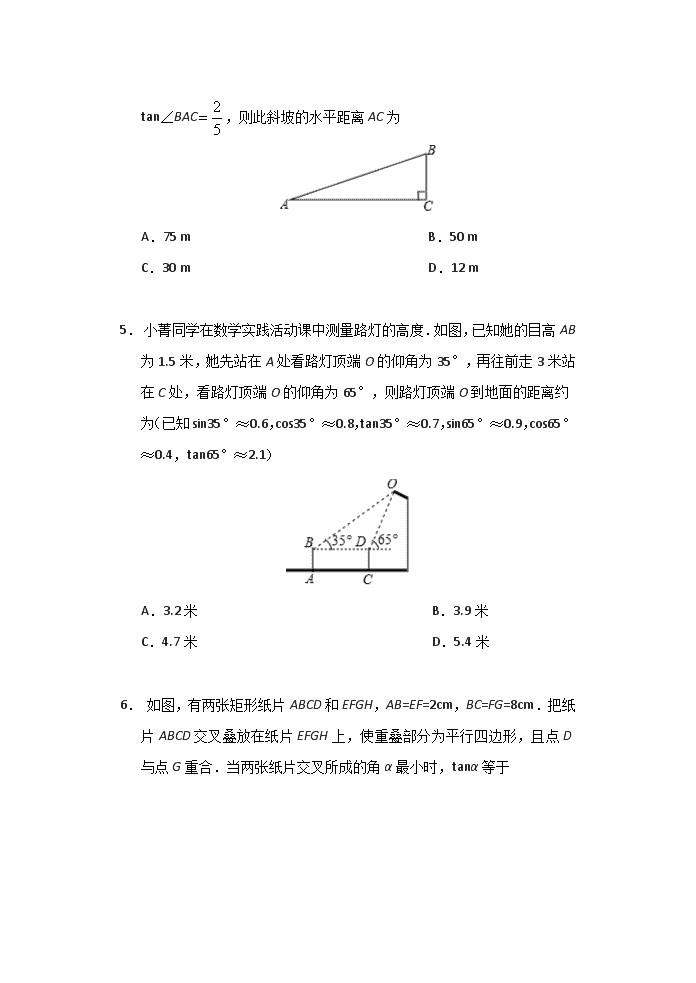
锐角三角函数 1. 在直角三角形ABC中,若2AB=AC,则cosC=__________. 2. 如图,某校教学楼AC与实验楼BD的水平间距CD=15米,在实验楼顶部B点测得教学楼顶部A点的仰角是30°,底部C点的俯角是45°,则教学楼AC的高度是________米(结果保留根号). 3. 如图,某海防哨所O发现在它的西北方向,距离哨所400米的A处有一艘船向正东方向航行,航行一段时间后到达哨所北偏东60°方向的B处,则此时这艘船与哨所的距离OB约为__________米.(精确到1米,参考数据:1.414,1.732) 4. 如图,有一斜坡AB,坡顶B离地面的高度BC为30 m,斜坡的倾斜角是∠BAC,若 tan∠BAC,则此斜坡的水平距离AC为 A.75 m B.50 m C.30 m D.12 m 5. 小菁同学在数学实践活动课中测量路灯的高度.如图,已知她的目高AB为1.5米,她先站在A处看路灯顶端O的仰角为35°,再往前走3米站在C处,看路灯顶端O的仰角为65°,则路灯顶端O到地面的距离约为(已知sin35°≈0.6,cos35°≈0.8,tan35°≈0.7,sin65°≈0.9,cos65°≈0.4,tan65°≈2.1) A.3.2米 B.3.9米 C.4.7米 D.5.4米 6. 如图,有两张矩形纸片ABCD和EFGH,AB=EF=2cm,BC=FG=8cm.把纸片ABCD交叉叠放在纸片EFGH上,使重叠部分为平行四边形,且点D与点G重合.当两张纸片交叉所成的角α最小时,tanα等于 A. B. C. D. 7. 定义:在等腰三角形中,底边与腰的比叫做顶角的正对,顶角A的正对记作sadA,即sadA=底边∶腰.如图,在△ABC中,AB=AC,∠A=4∠B.则cosB·sadA= A.1 B. C. D. 8. 如图所示,某施工队要测量隧道长度BC,AD=600米,AD⊥BC,施工队站在点D处看向B,测得仰角为45°,再由D走到E处测量,DE∥AC,ED=500米,测得仰角为53°,求隧道BC长.(sin53°≈,cos53°≈,tan53°≈). 9. 为了保证人们上下楼的安全,楼梯踏步的宽度和高度都要加以限制.中小学楼梯宽度的范围是260mm~300mm含(300mm),高度的范围是120mm~150mm(含150mm).如图是某中学的楼梯扶手的截面示意图,测量结果如下:AB,CD分别垂直平分踏步EF,GH,各踏步互相平行,AB=CD,AC=900mm,∠ACD=65°,试问该中学楼梯踏步的宽度和高度是否符合规定.(结果精确到1mm,参考数据:sin65°≈0.906,cos65°≈0.423) 10. 如图所示,某施工队要测量隧道长度BC,AD=600米,AD⊥BC,施工队站在点D处看向B,测得仰角为45°,再由D走到E处测量,DE∥AC,ED=500米,测得仰角为53°,求隧道BC长.(sin53°,cos53°,tan53°). 11. 墙壁及淋浴花洒截面如图所示.已知花洒底座A与地面的距离AB为170cm,花洒AC的长为30cm,与墙壁的夹角∠CAD为43°.求花洒顶端C到地面的距离CE(结果精确到1cm).(参考数据:sin43°=0.68,cos43°=0.73,tan43°=0.93) 12. 如图1为放置在水平桌面l上的台灯,底座的高AB为5cm,长度均为20cm的连杆BC,CD与AB始终在同一平面上. (1)转动连杆BC,CD,使∠BCD成平角,∠ABC=150°,如图2,求连杆端点D离桌面l的高度DE. (2)将(1)中的连杆CD再绕点C逆时针旋转,使∠BCD=165°,如图3,问此时连杆端点D离桌面l的高度是增加还是减少?增加或减少了多少?(精确到0.1cm,参考数据:1.41,1.73) 13. 如图,小明站在河岸上的G点,利用测角仪器DG测量小船C到岸边的距离,此时,测得小船C的俯角是∠FDC=30°,若测角仪器DG的高度是2米,BG=1米,BG平行于AC所在的直线,迎水坡AB的坡度i=4∶3,坡高BE=8米,求小船C到岸边的距离CA的长?(结果保留根号) 14. 如图所示,要在某东西走向的A、B两地之间修一条笔直的公路,在公路起点A处测得某农户C在A的北偏东68°方向上.在公路终点B处测得该农户c在点B的北偏西45°方向上.已知A、B两地相距2400米. (1)求农户c到公路B的距离;(参考数据:sin22°≈,cos22°≈,tan22°≈) (2)现在由于任务紧急,要使该修路工程比原计划提前4天完成,需将该工程原定的工作效率提高20%,求原计划该工程队毎天修路多少米? 答案 1. 或 2. 15+15 3. 567 4. A 5. C 6. D 7. B 8. 如图,在Rt△ABD中,AB=AD=600,作EM⊥AC于M, 则AM=DE=500,∴BM=100, 在Rt△CEM中,tan53°===,∴CM=800, ∴BC=CM–BM=800–100=700(米). 答:隧道BC长为700米. 9. 如图,连接BD,作DM⊥AB于点M, ∵AB=CD,AB,CD分别垂直平分踏步EF,GH, ∴AB∥CD,AB=CD, ∴四边形ABDC是平行四边形, ∴∠C=∠ABD,AC=BD, ∵∠C=65°,AC=900, ∴∠ABD=65°,BD=900, ∴BM=BD•cos65°=900×0.423≈381,DM=BD•sin65°=900×0.906≈815, ∵381÷3=127,120<127<150, ∴该中学楼梯踏步的高度符合规定, ∵815÷3≈272,260<272<300, ∴该中学楼梯踏步的宽度符合规定, 10. 在Rt△ABD中,AB=AD=600, 作EM⊥AC于M, 则AM-DE=500, ∴BM=100, 在Rt△CEM中,tan53°, ∴CM=800, ∴BC=CM-BM=800-100=700(米). 答:隧道BC长为700米. 11. 如图,过点C作CF⊥AB于F, 则∠AFC=90°, 在Rt△ACF中,AC=30,∠CAF=43°, ∵cos∠CAF=, ∴AF=AC•cos∠CAF=30×0.73=21.9, ∴CE=BF=AB+AF=170+21.9=191.9≈192(cm). 答:花洒顶端C到地面的距离CE为192cm. 12. (1)如图2中,作BO⊥DE于O. ∵∠OEA=∠BOE=∠BAE=90°, ∴四边形ABOE是矩形, ∴∠OBA=90°, ∴∠DBO=150°﹣90°=60°, ∴OD=BD•sin60°=20(cm), ∴DF=OD+OE=OD+AB=205≈39.6(cm). (2)如图3,作DF⊥l于F,CP⊥DF于P,BG⊥DF于G,CH⊥BG于H.则四边形PCHG是矩形, ∵∠CBH=60°,∠CHB=90°, ∴∠BCH=30°, ∵∠BCD=165°,∠DCP=45°, ∴CH=BCsin60°=10cm,DP=CDsin45°=10cm, ∴DF=DP+PG+GF=DP+CH+AB=(10105)(cm), ∴下降高度:DE﹣DF=205﹣10105=10103.2(cm). 13. ∵坡AB的坡度i=4∶3,坡高BE=8,∴AE=6, 由题意得,四边形BEHG为矩形, ∴GH=BE=8,EH=BG=2, ∴DH=DGDG+GH=9, 在Rt△DCH中,tanC=,则CH==9, ∴AC=CH-AE-EH=9-8, 答:小船C到岸边的距离CA的长为(9-8)米. 14. (1)如图,过C作CH⊥AB于H. 设CH=x, 由已知有∠EAC=68°,∠FBC=45°, 则∠CAH=22°,∠CBA=45°. 在Rt△BCH中,BH=CH=x, 在Rt△HAC中,tan∠HAC=, ∴HA=, ∵AH+HB=AB, ∴x+x=2400, 解得x=, ∴农户C到公路的距离米. (2)设原计划完成这项工程需要y天,则实际完成工程需要(y-4)天. 根据题意得:=(1+20%)×, 解得:y=24. 经检验知:y=24是原方程的根, 2400÷24=100(米). 答:原计划该工程队毎天修路100米. 查看更多