- 2021-11-10 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
湘教版九年级数学上册第四章测试题(含答案)
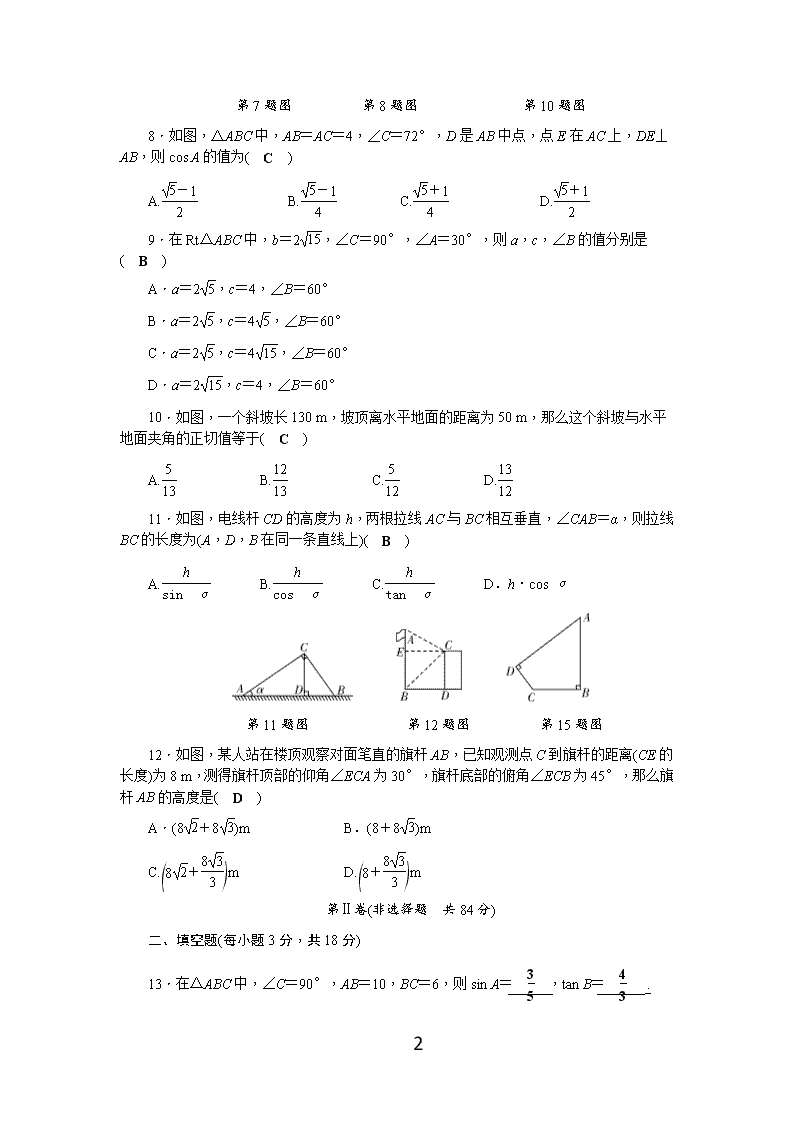
湘教版九年级数学上册第四章测试题(含答案) (考试时间:120分钟 满分:120分) 第Ⅰ卷(选择题 共36分) 一、选择题(每小题3分,共36分) 1.计算6tan 45°-2cos 60°的结果是( D ) A.4 B.4 C.5 D.5 2.在Rt△ABC中,∠C=90°,sin A=,则cos B的值等于( B ) A. B. C. D. 3.△ABC中,∠B=90°,AC=,tan C=,则BC边的长为( B ) A.2 B.2 C. D.4 4.在Rt△ABC中,∠ACB=90°,BC=1,AB=2,则下列结论正确的是( D ) A.sin A= B.tan A= C.cos B= D.tan B= 5.在平面直角坐标系xOy中,已知点A(2,1)和点B(1,0),则sin∠AOB的值等于( A ) A. B. C. D. 6.在△ABC中,(2cos A-)2+|1-tan B|=0,则△ABC一定是( D ) A.直角三角形 B.等腰三角形 C.等边三角形 D.等腰直角三角形 7.如图,在网格中,小正方形的边长均为1,点A,B,C都在格点上,则∠ABC的正切值是( D ) A.2 B. C. D. 第7题图 第8题图 第10题图 7 8.如图,△ABC中,AB=AC=4,∠C=72°,D是AB中点,点E在AC上,DE⊥AB,则cos A的值为( C ) A. B. C. D. 9.在Rt△ABC中,b=2,∠C=90°,∠A=30°,则a,c,∠B的值分别是( B ) A.a=2,c=4,∠B=60° B.a=2,c=4,∠B=60° C.a=2,c=4,∠B=60° D.a=2,c=4,∠B=60° 10.如图,一个斜坡长130 m,坡顶离水平地面的距离为50 m,那么这个斜坡与水平地面夹角的正切值等于( C ) A. B. C. D. 11.如图,电线杆CD的高度为h,两根拉线AC与BC相互垂直,∠CAB=α,则拉线BC的长度为(A,D,B在同一条直线上)( B ) A. B. C. D.h·cos α 第11题图 第12题图 第15题图 12.如图,某人站在楼顶观察对面笔直的旗杆AB,已知观测点C到旗杆的距离(CE的长度)为8 m,测得旗杆顶部的仰角∠ECA为30°,旗杆底部的俯角∠ECB为45°,那么旗杆AB的高度是( D ) A.(8+8)m B.(8+8)m C.m D.m 第Ⅱ卷(非选择题 共84分) 二、填空题(每小题3分,共18分) 13.在△ABC中,∠C=90°,AB=10,BC=6,则sin A= ,tan B= . 14.在Rt△ABC中,∠C=90°,当已知∠A和a时,求c,则∠A,a,c的关系式是c= . 7 15.如图,在四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tan A=,则CD= . 16.如图,某公园入口原有一段台阶,其倾角∠BAE=30°,高DE=2 m,为方便残疾人士,拟将台阶改成斜坡,设台阶的起点为A,斜坡的起点为C,现设计斜坡BC的坡度i=1∶5,则AC的长度是__(10-2)__m. 17.一艘轮船在小岛A的北偏东60°方向距小岛80海里的B处,沿正西方向航行3 h后到达小岛的北偏西45°的C处,则该船行驶的速度为 海里/小时. 18.△ABC中,AB=4,BC=3,∠BAC=30°,则△ABC的面积为__2+或2- . 三、解答题(共66分) 19.(6分)计算: (1)cos 45°-tan230°+tan 60°; 解:原式=·-+·=-+1=; (2)-+tan 45°. 解:原式=-+1 =+-+1 =+-1++1 =+. 20.(8分)在Rt△ABC中,∠C=90°,∠A,∠B,∠C的对边分别为a,b,c,根据下列条件进行计算: 7 (1)b=20,∠B=45°,求a,c; (2)a=50,b=50,求∠A,∠B. 解:(1)在Rt△ABC中,∠C=90°,∠B=45°,∴∠A=45°, ∴∠A=∠B,∴a=b=20. 又∵a2+b2=c2,∴c==20; (2)∵a=50,b=50,∴c==100. 又∵sin A===, ∴∠A=60°, ∠B=90°-∠A=30°. 21.(6分)已知a为锐角,且tan α是方程x2+2x-3=0的一个根,求2sin2α+cos2α-tan(α+15°)的值. 解:解方程x2+2x-3=0, 得x1=1,x2=-3. ∵tanα>0,∴tanα=1,∴α=45°, ∴2sin2α+cos2α-tan(α+15°)=2sin245°+cos245°-tan 60°=2×+-·=1+-3=-. 22.(8分)一个长方体木箱沿斜面下滑,当木箱滑至如图位置时,AB=3 m,已知木箱高BE=m,斜面坡角为30°,求木箱端点E距地面AC的高度EF. 解:连接AE. 在Rt△ABE中,AB=3 m,BE= m, ∴AE==2 m. 又∵tan∠EAB==, ∴∠EAB=30°. 在Rt△AEF中,∠EAF=∠EAB+∠BAC=60°, 7 ∴EF=AE·sin∠EAF=2× sin 60°=2× =3 m. 答:木箱端点E距地面AC的高度是3 m. 23.(8分)如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,sin B=,AD=1. (1)求BC的长; (2)求tan∠DAE的值. 解:(1)∵AD是BC边上的高, ∴AD⊥BC. 在Rt△ABD中,∵sin B==,AD=1, ∴AB=3,∴BD==2. 在Rt△ADC中,∵∠C=45°,∴CD=AD=1. ∴BC=2+1, (2)∵AE是BC边上的中线, ∴DE=-1=-, ∴tan∠DAE===-. 24.(9分)(乐山中考)如图,在水平地面上有一幢房屋BC与一棵树DE,在地面观察点A处测得屋顶C与树梢D的仰角分别是45°和60°,∠CAD=60°,在屋顶C处测得∠DCA=90°.若房屋的高BC=6 m,求树高DE的长度. 解:如图,在Rt△ABC中, 7 ∠CAB=45°,BC=6 m. ∴AC==6 m. 在Rt△ACD中,∠CAD=60°, ∴AD==12 m; 在Rt△DEA中,∠EAD=60°. DE=AD·sin 60°=12·=6 m. 答:树DE的高为6 m. 25.(10分)(青岛中考)如图,C地在A地的正东方向,因有大山阻隔,由A地到C地需要绕行B地,已知B位于A地北偏东67°方向,距离A地520 km,C地位于B地南偏东30°方向,若打通穿山隧道,建成两地直达高铁,求A地到C地之间高铁线路的长.(结果保留整数)(参考数据:sin 67°≈,cos 67°≈,tan 67°≈,≈1.73) 解:如图,作BD⊥AC于点D, 在Rt△ABD中, ∠ABD=67°,sin 67°=≈. ∴AD≈AB=480 km,cos 67°=≈, ∴BD≈AB=200 km. 在Rt△BCD中,∠CBD=30°, tan 30°==, ∴CD=BD≈115 km, AC=AD+CD=595 km. 7 答:AC之间的距离约为595 km. 26.(11分)(荆州中考)如图,某数学活动小组为测量学校旗杆AB的高度,沿旗杆正前方2米处的点C出发,沿斜面坡度i=1∶的斜坡CD前进4米到达点D,在点D处安置测角仪,测得旗杆顶部A的仰角为37°,量得仪器的高DE为1.5米.已知A,B,C,D,E在同一平面内,AB⊥BC,AB∥DE.求旗杆AB的高度.(参考数据:sin 37°≈,cos 37°≈,tan 37°≈.计算结果保留根号) 解:延长ED交BC的延长线于点F, 则∠CFD=90°, ∵tan∠DCF=i==, ∴∠DCF=30°. ∵CD=4, ∴DF=CD=2,CF=CD·cos∠DCF=4× =2, ∴BF=BC+CF=2+2=4, 过点E作EG⊥AB于点G, 则GE=BF=4. GB=EF=ED+DF=1.5+2=3.5. 又∵∠AEG=37°, ∴AG=GE·tan∠AEG=4·tan 37°, 则AB=AG+BG=4·tan 37°+3.5=3+3.5. 故旗杆AB的高度为(3+3.5)米. 7查看更多