平行线分线段成例教案1

平行线分线段成例教案1

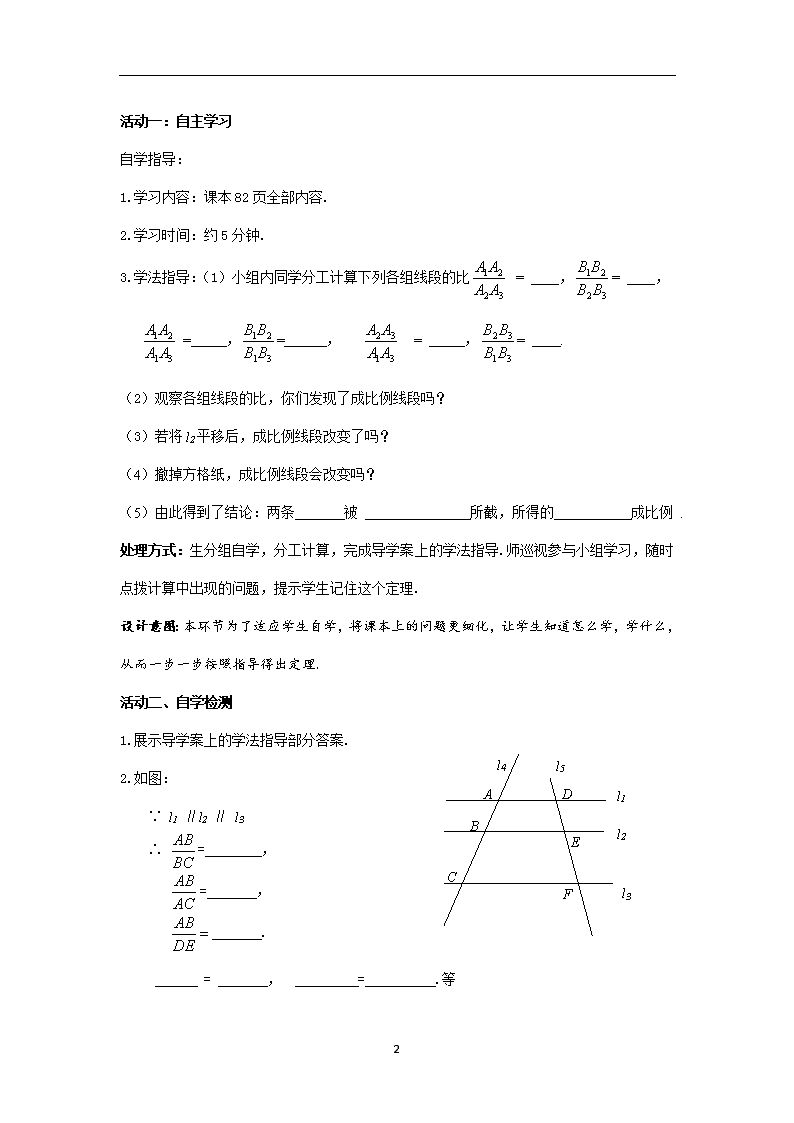
课题：4.2 平行线分线段成比例 教学目标：‎ ‎1.经历平行线分线段成比例基本事实及推论的探索过程，掌握这两个定理.‎ ‎2.会应用定理及推论求线段的长度或证明线段间的关系.‎ 教学重、难点：‎ 重点：平行线分线段成比例定理及推论的掌握与应用.‎ 难点：熟练运用平行线分线段成比例定理及其推论进行计算.‎ 教学过程：‎ 一、创设情境，引入新课 活动内容：回答下列问题.‎ 问题1.线段的比如何计算？‎ 问题2.线段AB、CD、EF、GH成比例是什么意思？‎ 问题3：教师展示绳子 ‎（1）你能快速的将这根绳子分成相等的两根吗？‎ ‎（2）你能快速的将它分成长度比为1:3的两根吗？‎ ‎（3）你能快速的将它分成长度比为2:3的两根吗？‎ 处理方式：问题1、2由学生口答完成.（教师注意学生回答问题1时对长度的叙述，回答问题2时四条线段的顺序性是否正确）.问题3由学生自告奋勇动手分一分试一试，一学生操作，其他同学进行判断. ‎ 设计意图：本环节通过对线段的比及成比例线段的复习，为这节课的探究活动做铺垫.设计问题3，学生对前两种分法都很轻松，到了第3中将会产生疑问或分的不准确，提出这个问题是为了让学生感受到数学对解决生活中问题的必要性.为本节课的学习设下悬念，激发学生的学习兴趣.‎ 二、探究学习，感悟新知 7‎ 活动一：自主学习 自学指导：‎ ‎1.学习内容：课本82页全部内容.‎ ‎2.学习时间：约5分钟.‎ ‎3.学法指导：（1）小组内同学分工计算下列各组线段的比 = ，= ，‎ ‎ = ，= ， = ，= . ‎ ‎（2）观察各组线段的比，你们发现了成比例线段吗？‎ ‎（3）若将l2平移后，成比例线段改变了吗？‎ ‎（4）撤掉方格纸，成比例线段会改变吗？‎ ‎（5）由此得到了结论：两条 被 所截，所得的 成比例 .‎ 处理方式：生分组自学，分工计算，完成导学案上的学法指导.师巡视参与小组学习，随时点拨计算中出现的问题，提示学生记住这个定理.‎ 设计意图：本环节为了适应学生自学，将课本上的问题更细化，让学生知道怎么学，学什么，从而一步一步按照指导得出定理.‎ 活动二、自学检测 l1‎ l2‎ l3‎ l5‎ l4‎ C B F E D A ‎1.展示导学案上的学法指导部分答案. ‎ ‎2.如图： ‎ ‎ ∵ l1 ∥l2 ∥ l3 ‎ ‎ ∴ = ， ‎ ‎ = ， ‎ ‎ .‎ ‎ = ， = .等 7‎ 处理方式：将一位同学导学案上的学法指导部分的答案借助实物投影投出，全体同学进行批改订正，形成结论.第二问由学生将比例写在黑板上.多名同学相互补充，感受对应线段成比例的不同表示方法.‎ 活动三、合作探究（一）‎ ‎1.你认为定理中的关键词是 ？‎ ‎2.在找出“对应线段”时你有什么好方法与同学们分享？‎ 处理方式：师将平行和对应线段画出来，以示本定理的关键.同时强调这是使用本定理的条件和书写比例时必须注意的问题.各小组各抒己见，说出找对应线段的技巧及比例的书写技巧.‎ 设计意图：本环节主要是深化学生对平行线分线段成比例定理的理解，预防学生在解决问题时只写比例式而忽略了平行线这个条件，再者让学生明确无论是上下比还是左右比，都必须对应.‎ 跟踪训练（一）‎ ‎1.如图，已知两条直线被三条平行线所截，截得的线段长度如图所示，则x= .‎ C B F E D A ‎2.如图，直线l1 ∥l2 ∥ l3 ，另两条直线分别交l1 ，l2 ， l3于点A，B，C及点D，E，F，且AB=3，DE=4，EF=2，则BC= .‎ l1‎ ‎ ‎ ‎4‎ ‎3‎ ‎ ‎ l2‎ ‎7‎ x ‎ ‎ l3‎ ‎ ‎ ‎ 第1题 第2题 处理方式：学生独立完成这两个习题，小组内的同学相互批改.‎ 设计意图：借助这两个小题检测学生对定理的理解，发现定理只对“平行”和“对应”有限制，而与被截直线的位置无关.同时借助于比例式，求线段的长.‎ 7‎ 活动四、合作探究（二）‎ 提出问题：1.将直线l5向左平移，使其与l4相交于A点（如左图），则上述比例还成立吗？‎ ‎2. 将直线l5继续向左平移，使其与l4相交于B点（如右图），则上述比例还成立吗？‎ l5‎ A B C D F l1‎ l2‎ l3‎ l4‎ l5‎ A B C E F l1‎ l2‎ l3‎ l4‎ l5‎ A B C D F l1‎ l2‎ l3‎ l4‎ l5‎ A B C E F l1‎ l2‎ l3‎ l4‎ ‎3.平行线分线段成比例定理与两直线的位置有关系吗？‎ ‎4.（擦掉多余直线），观察这两个图形，上述比例式还成立吗？你发现了什么？‎ ‎5.推论： 三角形一边的直线与其它两边相交， .‎ ‎6. ∵ ，‎ ‎∴ .‎ 处理方式：学生分组讨论，完成自学提出的问题.师参与学生的讨论，并给出适当的点拨.学生在讨论时指出对应线段，各小组派代表将符号语言板书在黑板上.‎ 三、例题解析，应用新知 例：如图，在△ABC中，E、F分别是AB和AC上的点，且EF∥BC.‎ A B C E F ‎（1）如果AE=7，EB=5，FC=4，那么AF的长是多少？‎ ‎（2）如果AB=10，AE=6，AF=5，那么FC的长是多少？‎ 处理方式：‎ 7‎ 生思考2分钟，然后试着写出求解过程，生主动去黑板上板演，小组内的其他同学主动订正，最后师进行评价，给出规范的板书.‎ 设计意图：通过本题的解答，让学生感悟到平行线分线段成比例定理的推论的应用，选择恰当的比例式，并以此为例，给出规范书写.‎ A B C D E 跟踪训练（二）‎ 如图，在△ABC中，D、E分别是AB和AC上的点，且DE∥BC.‎ ‎（1）如果AD=15，AB=40，AC=28，那么AE= .‎ ‎（2）如果AB=5，AD=3，AC=4，那么EC= .‎ 处理方式：两生板演，生分组训练，互相批改.教师及时表扬鼓励.‎ 设计意图：学生已经对例题学习完毕，是否会根据条件和结论写出合适的比例对学生来说是个挑战，教师也借这两题看看学生对定理的灵活应用情况，及时获得反馈信息，解决学生学习中的问题.‎ 四、拓展应用，答疑解惑 提出问题：现在你能解决将绳子分为2:3两根这个问题吗？‎ 处理方式：生分组讨论，师巡视，参与小组讨论，倾听他们的见解，并给与启发性点拨，搜集不同小组的不同答案，待会进行展示.‎ 设计意图：解决课堂开始时的疑问，感受数学在生活中的应用，并会设计n等分线段的方法.‎ 五、回顾反思，提炼升华 ‎“学而不思则罔”，本节课你有哪些收获和疑问，谈谈你的看法.‎ 处理方式：鼓励学生大胆回答畅谈，说出自己所学到的知识及解题技巧和问题解决中的突破口，让全体同学在知识上，方法上，技巧上均有收获.‎ 设计意图：通过学生总结收获，对本节课的学习内容强化记忆，在解题中形成技巧.‎ 六、达标检测，反馈提高 A组：如图，已知直线l1 ∥l2 ∥ l3，‎ ‎（1）在图（1）中，AB=5，BC=7，EF=4，那么DE= .‎ 7‎ ‎（2）在图（2）中，DE=6，AB=5，EF=7，那么AC= .‎ l1‎ l2‎ l333‎ l5‎ l4‎ C B F E D A E l5‎ A B C D F l1‎ l2‎ l3‎ l4‎ ‎ （1） （2）‎ A B C D E 考查知识点：平行线分线段成比例定理的基本应用 ‎2.如图，已知DE∥BC，如果AB=10，AD=6，AE=5，那么EC= .‎ 考查知识点：平行线分线段成比例定理的推论 F A B C D E B组：‎ 如图，已知在△ABC中，点E、D、F分别在AB、AC和BC上，DE∥BC，DF∥AB，试判断成立吗？‎ 考查知识点：平行线分线段成比例定理的应用及转化 处理方式：学生独立完成，然后教师将一生的答案投出来，同学们积极发表见解，进行批改订正.‎ 设计意图：通过这三个小题，检测学生对本节课的学习情况，及时反馈，查缺补漏.‎ 板书设计 ‎§4.2平行线分线段成比例 7‎ 跟踪训练（二）学生展示区 定理：‎ 推论推导区：‎ 推论：‎ 例题 跟踪训练（二）学生展示区 7‎