- 2021-11-10 发布 |
- 37.5 KB |
- 4页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2011初三数学二模题-丰台
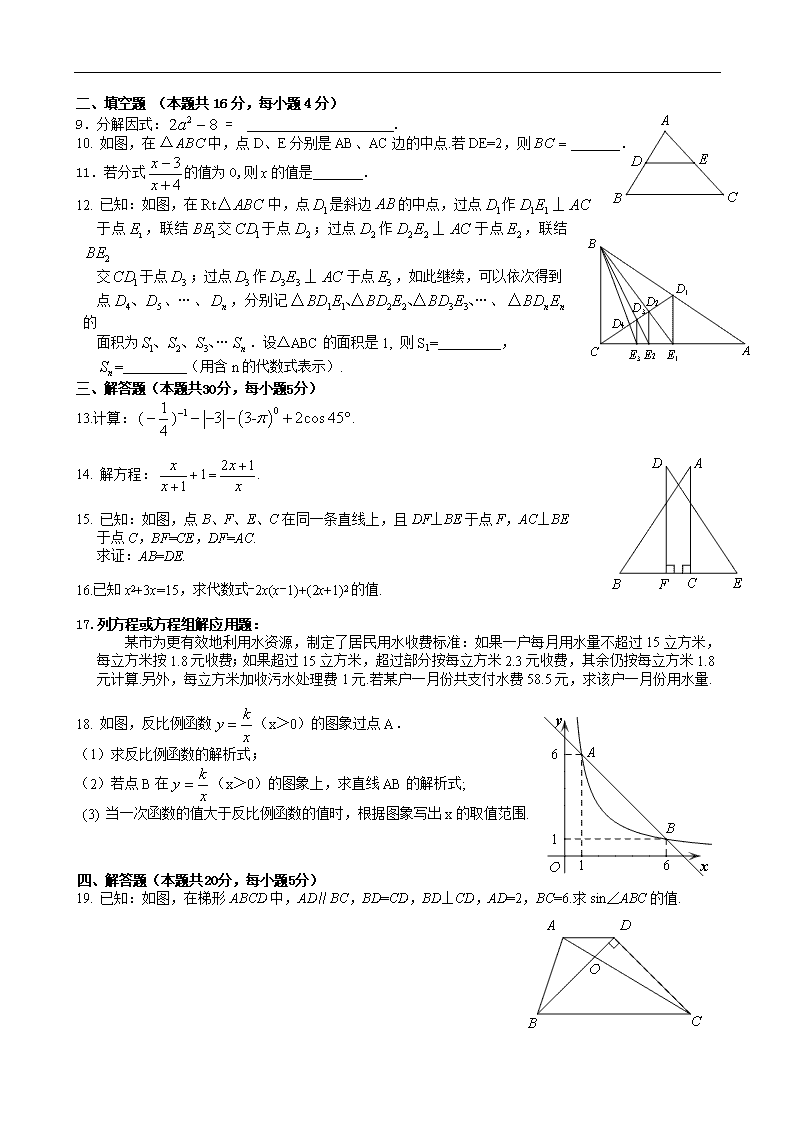
丰台区2011年初三统一练习(二) 数 学 试 卷 2011.6. 学校 姓名 考号 考 生 须 知 1.本试卷共6页,共五道大题,25道小题,满分120分.考试时间120分钟. 2.在试卷和答题卡上认真填写学校名称、姓名和考号. 3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效. 4.在答题卡上,选择题、作图题用2B铅笔作答,其他试题用黑色字迹签字笔作答. 5.考试结束,将本试卷、答题卡和草稿纸一并交回. 一、选择题 (本题共32分, 每小题4分) 下列各题均有四个选项,其中只有一个是符合题意的 1.的相反数是 A.5 B. C. D. 2. 根据北京缓解拥堵网站公布的数据,截止2011年4月9日零时,北京小客车指标个人申请累计约为492000个,用科学记数法表示492000是 A. B. C. D. 3. 若一个正多边形的每个内角都为120°,则这个正多边形的边数是 A.9 B.8 C.7 D.6 4. 一个扇形的圆心角为90°,半径为2,则这个扇形的面积是 A.6 B. 4 C. 2 D. 5.在五张质地大小完全相同的卡片上分别印有直角三角形、平行四边形、菱形、正方形、等腰梯形的图案,现将印有图案的一面朝下,混合后从中随机抽取一张,则抽到的卡片上的图案既是轴对称图形又是中心对称图形的概率是 A. B. C. D. 6.如图,BD是⊙O的直径,∠CBD=,则∠A的度数是 A.30 B.45 C.60 D.75 7. 某居民小区开展节约用电活动,有关部门对该小区100户家庭的节电量情况进行了统计, 4月份与3月份相比,节电量情况如下表: 节电量(千瓦时) 20 30 40 50 户 数 10 40 30 20 则4月份这100户家庭节电量的中位数、众数分别是 A. 35、30 B. 30、20 C. 30、35 D. 30、30 8.如图所示的正方体的展开图是( ) A. B. C. D. 二、填空题 (本题共16分,每小题4分) 9.分解因式: = . 10. 如图,在中,点D、E分别是AB、AC边的中点.若DE=2,则 . 11.若分式的值为0,则x的值是 . 12. 已知:如图,在中,点是斜边的中点,过点作 于点,联结交于点;过点作于点,联结 交于点;过点作于点,如此继续,可以依次得到 点、…、,分别记…、的 面积为….设△ABC的面积是1, 则S1= , = (用含n的代数式表示). 三、解答题(本题共30分,每小题5分) 13.计算:. 14. 解方程:. 15. 已知:如图,点B、F、E、C在同一条直线上,且DF⊥BE于点F,AC⊥BE 于点C,BF=CE,DF=AC. 求证:AB=DE. 16.已知x2+3x=15,求代数式-2x(x-1)+(2x+1)2的值. 17.列方程或方程组解应用题: 某市为更有效地利用水资源,制定了居民用水收费标准:如果一户每月用水量不超过15立方米,每立方米按1.8元收费;如果超过15立方米,超过部分按每立方米2.3元收费,其余仍按每立方米1.8元计算.另外,每立方米加收污水处理费1元.若某户一月份共支付水费58.5元,求该户一月份用水量. 18. 如图,反比例函数(x>0)的图象过点A. (1)求反比例函数的解析式; (2)若点B在(x>0)的图象上,求直线AB的解析式; (3) 当一次函数的值大于反比例函数的值时,根据图象写出x的取值范围. 四、解答题(本题共20分,每小题5分) 19. 已知:如图,在梯形ABCD中,AD∥BC,BD=CD,BD⊥CD,AD=2,BC=6.求sin∠ABC的值. 20. 已知:如图,在Rt△ABC中,∠C=90°,点E在斜边AB上,以AE为直径的⊙O与BC边相切于点D,联结AD. (1)求证:AD是∠BAC的平分线; (2)若AC= 3,tan B=,求⊙O的半径. 21. 某校数学兴趣小组成员小华对本班上学期期末考试数学成绩(成绩取整数,满分为100分)作了统计分析,绘制成如下频数分布表和频数分布直方图.请你根据图表提供的信息,解答下列问题: (1)频数分布表中a= ,b= ; (2)补全频数分布直方图; (3)数学老师准备从不低于90分的学生中选1人介绍学习经验,那么取得了93分的小华被选上的概率是多少? 频数分布表 分组(分) 频数 频率 50~60 2 0.04 60~70 a 0.16 70~80 20 0.40 80~90 16 0.32 90~100 4 b 合计 50 1 22. 猜想、探究题: (1)观察与发现 小明将三角形纸片沿过点A的直线折叠,使得AC落在AB边上,折痕为AD,展开纸片(如图①);再次折叠该三角形纸片,使点A和点D重合,折痕为EF,展平纸片后得到(如图②).你认为是什么形状的三角形? A C D B 图① A C D B 图② F E (2)实践与运用 将矩形纸片(AB<CD)沿过点B的直线折叠,使点A落在BC边上的点F处,折痕为BE(如图③);再沿过点E的直线折叠,使点D落在BE上的点处,折痕为EG(如图④);再展平纸片(如图⑤). 猜想△EBG的形状,证明你的猜想,并求图⑤中∠FEG的大小. 五、解答题(本题共22分,第23题7分,第24题8分,第25题7分) 23. 已知:关于x的方程. (1)求证:方程总有实数根; (2)当k取哪些整数时,关于x的方程的两个实数根均为负整数? 24. 已知:矩形OABC的顶点O在平面直角坐标系的原点,边OA、OC分别在x、y轴的正 半轴 上,且OA=3cm,OC=4cm,点M从点A出发沿AB向终点B运动,点N从点C 出发沿CA向终点A运动,点M、N同时出发,且运动的速度均为1cm/秒,当其中一个点 到达终点时,另一点即停止运动.设运动的时间为t秒. (1)当点N运动1秒时,求点N的坐标; (2)试求出多边形OAMN的面积S与t的函数关系式; (3)t为何值时,以△OAN的一边所在直线为对称轴翻折△OAN,翻折前后的两个三角形 所组成的四边形为菱形. 25. 已知:如图,二次函数图象的顶点坐标为C(1,-2),直线的图象与该二次函数的图象交于两点,其中点坐标为(3,0),点在轴上.点为线段上的一个动点(点与点不重合),过点且垂直于轴的直线与这个二次函数的图象交于点. (1)求这个二次函数的解析式; (2)设点的横坐标为,求线段的长(用含x 的代数式表示); (3)点为直线与这个二次函数图象对称轴的交点,若以点为顶点的三角形与△AOB 相似,请求出点的坐标.查看更多