中考数学总复习专题课件：相交弦定理切割线定理2

中考数学总复习专题课件：相交弦定理切割线定理2

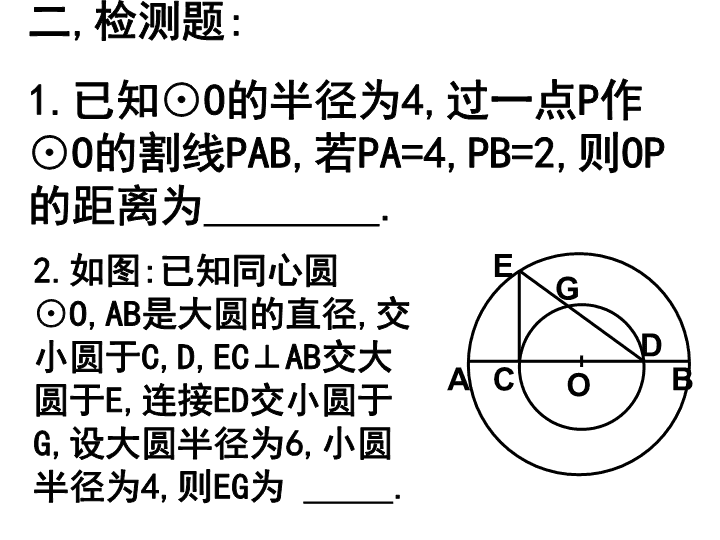
复习之五 相交弦定理 切割线定理 一 . 复习目标 : 1. 熟练掌握相交弦定理及其应用 . 2. 熟练掌握切割线定理及其应用 . 3. 掌握与其它知识的联系 , 综合应用 . 4. 熟练掌握割线定理及其应用 . 二 , 检测题 : 1. 已知 ⊙ O 的半径为 4, 过一点 P 作 ⊙ O 的割线 PAB, 若 PA=4,PB=2, 则 OP 的距离为 . 2. 如图 : 已知同心圆 ⊙ O,AB 是大圆的直径 , 交小圆于 C,D,EC⊥AB 交大圆于 E, 连接 ED 交小圆于 G, 设大圆半径为 6, 小圆半径为 4, 则 EG 为 . A B C D O E G 3. 如图 :⊿ABC 是 ⊙ O 的内接正三角形 , 弦 PQ 过 AB,AC 的中点 D,E, 求 PQ:BC 的值 . A B C D E P Q A B C D P M N O 4. 如图 : 已知 AD 切 ⊙ O 于 D, 割线 ACB 交 ⊙ O 于点 C,B, 线段 AP=AD,PC 交 ⊙ O 于 N,PB 交 ⊙ O 于 M, 求证 :MN∥PA 5. 已知如图 , ⊙O 的直径 AB 的延长线与弦 CD 的延长线相交于 P,E 为 ⊙ o 上一点 , AE=AC,DE 交 AB 于点 F, 求证 :PF×PO=PA×PB A P B C D E F O A B O P C 二 . 课堂练习 : 1. 如图 :P 是半径为 2 的 ⊙ O 内的一点 ,OP= ,AB 经过 P 点的弦 , 过点 A,B 分别作 ⊙ O 的切线 AC 和 BC 交于 C 点 , 设 P 点到 AC,BC 的距离分别为 a,b , ∠AOB=2 ( 为锐角 ), 求证 : (1)a,b 是关于 x 的方程 的两个根 . (2) 当 时 ,P 点恰好在线段 OC 上 .