江西专版2020中考数学复习方案第六单元圆第25课时与圆有关的位置关系课件
第
25
课时
与圆有关的位置关系
第六单元 圆
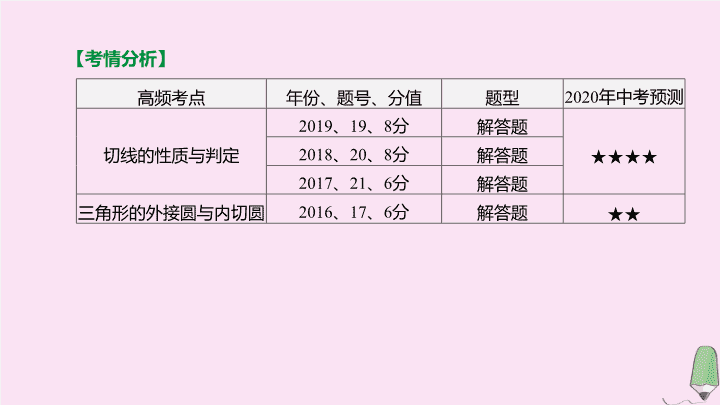
【
考情分析
】
高频考点
年份、题号、分值
题型
2020
年中考预测
切线的性质与判定
2019
、
19
、
8
分
解答题
★★★★
2018
、
20
、
8
分
解答题
2017
、
21
、
6
分
解答题
三角形的
外接圆
与内切圆
2016
、
17
、
6
分
解答题
★★
如果圆的半径是
r
,
点到圆心的距离是
d
,
那么
点在圆外
⇔
①
点在圆上
⇔
②
点在圆内
⇔
③
考点一 点和圆的位置关系
考点聚焦
d>r
d=r
d
=
<
切线的性质
圆的切线
⑦
过切点的半径
推论
(1)
经过圆心且垂直于切线的直线必过
⑧
(2)
经过切点且垂直于切线的直线必过
⑨
切线的判定
(1)
和圆只有
⑩
个公共点的直线是圆的切线
(2)
如果圆心到一条直线的距离等于圆的
⑪
,
那么这条直线是圆的切线
(3)
经过半径的外端并且
⑫
这条半径的直线是圆的切线
常添辅助线
连接圆心和切点
考点三 切线的性质与判定
垂直于
切点
圆心
一
半径
垂直于
切线长
经过圆外一点的圆的切线上
,
这点和切点之间线段的长
,
叫做这点到圆的切线长
切线长定理
从圆外一点可以引圆的两条切线
,
它们的切线长
⑬
,
这一点和圆心的连线
⑭
两条切线的夹角
基本图形
点
P
是
☉
O
外一点
,
PA
,
PB
分别切
☉
O
于点
A
,
B
,
AB
交
PO
于点
C
,
则有如下结论
:
(1)
PA=PB
;
(2)
∠
APO=
∠
BPO=
∠
OAC=
∠
OBC
,
∠
AOP=
∠
BOP=
∠
CAP=
∠
CBP
考点四 切线长与切线长定理
相等
平分
外接圆
内切圆
图形
定义
经过三角形的三个顶点的圆
与三角形各边都相切的圆
圆心
O
外心
(
三角形三条边
的
⑮
的
交点
)
内心
(
三角形三个内角的
⑯
的交点
)
性质
三角形的外心到三角形的三个顶点的距离相等
三角形的内心到三角形的三条边的距离相等
考点五 三角形的外接圆与内切圆
垂直平分线
角平分线
(续表)
画法
作三角形任意两边的垂直平分线
,
其交点即为圆心
O
,
以圆心
O
到任一顶点的距离为半径作
☉
O
即可
作三角形任意两角的平分线
,
其交点即为圆心
O
,
过点
O
作任一边的垂线段作为半径
,
作
☉
O
即可
图
25
-1
题组一 必会题
对点演练
1
.
已知☉
O
的半径为
5,
若
OP=
6,
则点
P
与☉
O
的位置关系是
(
)
A
.
点
P
在☉
O
内
B
.
点
P
在☉
O
上
C
.
点
P
在☉
O
外
D
.
无法判断
C
2
.
如图
25-2,
∠
O=
30°,
C
为
OB
上一点
,
且
OC=
6,
以点
C
为圆心
,3
为半径的圆与直线
OA
的位置关系是
(
)
A
.
相离
B
.
相交
C
.
相切
D
.
以上三种情况均有可能
图
25-2
C
3
.
[2019·
无锡
]
如图
25-3,
PA
是☉
O
的切线
,
切点为
A
,
PO
的延长线交☉
O
于点
B
,
若∠
P=
40°,
则∠
B
的度数为
(
)
A
.
20° B
.
25° C
.
40° D
.
50°
图
25-3
B
图
25-4
[
答案
]A
图
25-5
[
答案
]A
题组二 易错题
【
失分点
】
在图形不明确的情况下
,
判断点或直线与圆的位置关系时
,
忽视分类讨论而漏解
;
三角形的外接圆与三角形的内切圆的概念混淆
.
图
25-6
[
答案
]B
7
.
已知一个点到圆上的点的最大距离是
5,
最小距离是
1,
则这个圆的直径是
.
[
答案
]
6
或
4
[
解析
]
分两种情况
:
当点
M
在圆内时
,
如图①
,
∵点到圆上的最小距离
MB=
1,
最大距离
MA=
5,
∴直径
AB=
1+5
=
6;
当点
M
在圆外时
,
如图②
,
∵点到圆上的最小距离
MB=
1,
最大距离
MA=
5,
∴直径
AB=
5-1
=
4
.
8
.
[2019·
宁波
]
如图
25-7,Rt△
ABC
中
,
∠
C=
90°,
AC=
12,
点
D
在边
BC
上
,
CD=
5,
BD=
13
.
点
P
是线段
AD
上一动点
,
当半径为
6
的☉
P
与
△
ABC
的一边相切时
,
AP
的长为
.
图
25-7
考向一 切线的性质的相关证明与计算
例
1
[2019·
新疆生产建设兵团
]
如图
25-8,
AB
是☉
O
的直径
,
CD
与☉
O
相切于点
C
,
与
AB
的延长线交于点
D
,
CE
⊥
AB
于点
E
,
连接
BC.
(1)
求证
:
∠
BCE=
∠
BCD
;
(2)
若
AD=
10,
CE=
2
BE
,
求☉
O
的半径
.
图
25-8
解
:(1)
证明
:
如图①
,
连接
OC.
∵
CD
与☉
O
相切于点
C
,
∴∠
OCD=
90°
.
∴∠
OCB
+
∠
BCD=
90°
.
∵
CE
⊥
AB
,
∴∠
OBC
+
∠
BCE=
90°
.
∵
OC=OB
,
∴∠
OCB=
∠
OBC.
∴∠
BCE=
∠
BCD.
例
1
[2019·
新疆生产建设兵团
]
如图
25-8,
AB
是☉
O
的直径
,
CD
与☉
O
相切于点
C
,
与
AB
的延长线交于点
D
,
CE
⊥
AB
于点
E
,
连接
BC.
(2)
若
AD=
10,
CE=
2
BE
,
求☉
O
的半径
.
图
25-8
【
方法点析
】
(1)
条件中出现切线
,
要想到连接过切点的半径
,
由切线的性质可得直角三角形
,
利用直角三角形的性质和勾股定理解决问题
;(2)
若两个直角三角形有公共边或相等的边或两边之间有数量关系
,
则可利用勾股定理构建方程解决问题
.
1
.
[2019·
重庆
B
卷
]
如图
25-9,
AB
是☉
O
的直径
,
AC
是☉
O
的切线
,
A
为切点
,
若∠
C=
40°,
则∠
B
的度数为
(
)
A
.
60° B
.
50° C
.
40° D
.
30°
|
考向精练
|
B
图
25-9
图
25-10
[
答案
]B
图
25-11
[
答案
]
144
[
解析
]
∵☉
O
与正五边形
ABCDE
的边
AB
,
DE
分别相切于点
B
,
D
,
∴
OB
⊥
AB
,
OD
⊥
DE
,
∵正五边形每个内角为
108°,
∴∠
O=
∠
C
+
∠
OBC
+
∠
ODC =
108°×3-90°×2
=
144°
.
图
25-12
解
:(1)
证明
:
连接
OC
,
如图
.
∵
CD
是☉
O
的切线
,
∴
OC
⊥
CD
,
∴∠
OCD=
90°,
∴∠
DCA=
90°-
∠
OCA.
又∵
PE
⊥
AB
,
点
D
在
EP
的延长线上
,
∴∠
DEA=
90°,
∴∠
DPC=
∠
APE=
90°-
∠
OAC.
∵
OA=OC
,
∴∠
OCA=
∠
OAC.
∴∠
DCA=
∠
DPC
,
∴
DC=DP.
图
25-12
考向二 切线的判定及相关计算
图
25-13
例
2
[2019·
江西
19
题
]
如图
25-13
①
,
AB
为半圆的直径
,
点
O
为圆心
,
AF
为半圆的切线
,
过半圆上的点
C
作
CD
∥
AB
交
AF
于点
D
,
连接
BC.
(1)
连接
DO
,
若
BC
∥
OD
,
求证
:
CD
是半圆的切线
;
(2)
如图②
,
当线段
CD
与半圆交于点
E
时
,
连接
AE
,
AC
,
判断∠
AED
和∠
ACD
的数量关系
,
并证明你的结论
.
解
:(1)
证明
:
如图①
,
连接
OC.
∵
CD
∥
AB
,
BC
∥
OD
,
∴四边形
BODC
是平行四边形
,
∴
BC=OD
,
∠
CBO=
∠
DOA.
又∵
BO=OA
,
∴
△
CBO
≌△
DOA
,
∴∠
BOC=
∠
OAD.
∵
AF
为半圆的切线
,
∴∠
OAD=
90°,
∴∠
BOC=
90°
.
∵
CD
∥
AB
,
∴∠
OCD=
90°
.
∵
OC
是☉
O
的半径
.
∴
CD
是半圆的切线
.
图
25-13
例
2
[2019·
江西
19
题
]
如图
25-13
①
,
AB
为半圆的直径
,
点
O
为圆心
,
AF
为半圆的切线
,
过半圆上的点
C
作
CD
∥
AB
交
AF
于点
D
,
连接
BC.
(2)
如图②
,
当线段
CD
与半圆交于点
E
时
,
连接
AE
,
AC
,
判断∠
AED
和∠
ACD
的数量关系
,
并证明你的结论
.
【
方法点析
】
切线的判定方法
:
(1)
如果直线和圆有公共点
,
常连接这个公共点和圆心
,
得到半径
,
再说明这条半径和直线垂直
,
此直线即圆的切线
(
简记为
“
有公共点连半径
,
证垂直
”);
(2)
如果不确定直线与圆是否有公共点
,
常过圆心作这条直线的垂线
,
若垂线段的长等于半径长
,
则该直线是圆的切线
(
简记为
“
无公共点
,
作垂线
,
证相等
”)
.
|
考向精练
|
1
.
[2014·
江西
22
题
]
如图
25-14
①
,
AB
是☉
O
的直径
,
点
C
在
AB
的延长线上
,
AB=
4,
BC=
2,
P
是☉
O
上半部分的一个动点
,
连接
OP
,
CP.
(1)
求
△
OPC
的最大面积
;
(2)
求∠
OCP
的最大度数
;
(3)
如图②所示
,
延长
PO
交☉
O
于点
D
,
连接
DB
,
当
CP=DB
时
,
求证
:
CP
是☉
O
的切线
.
图
25-14
1
.
[2014·
江西
22
题
]
如图
25-14
①
,
AB
是☉
O
的直径
,
点
C
在
AB
的延长线上
,
AB=
4,
BC=
2,
P
是☉
O
上半部分的一个动点
,
连接
OP
,
CP.
(2)
求∠
OCP
的最大度数
;
图
25-14
1
.
[2014·
江西
22
题
]
如图
25-14
①
,
AB
是☉
O
的直径
,
点
C
在
AB
的延长线上
,
AB=
4,
BC=
2,
P
是☉
O
上半部分的一个动点
,
连接
OP
,
CP.
(3)
如图②所示
,
延长
PO
交☉
O
于点
D
,
连接
DB
,
当
CP=DB
时
,
求证
:
CP
是☉
O
的切线
.
图
25-14
图
25-15
图
25-15
图
25-15
图
25-16
图
25-16
考向三 与圆相关的创新作图
例
3
[2015·
江西
17
题
]
☉
O
为
△
ABC
的外接圆
,
请仅用无刻度的直尺
,
根据下列条件分别在图
25-17
①
,
②中画出一条弦
,
使这条弦将
△
ABC
分成面积相等的两部分
(
保留作图痕迹
,
不写作法
)
.
(1)
如图
25-17
①
,
AC=BC
;
(2)
如图
25-17
②
,
直线
l
与☉
O
相切于点
P
,
且
l
∥
BC.
图
25-17
例
3
[2015·
江西
17
题
]
☉
O
为
△
ABC
的外接圆
,
请仅用无刻度的直尺
,
根据下列条件分别在图
25-17
①
,
②中画出一条弦
,
使这条弦将
△
ABC
分成面积相等的两部分
(
保留作图痕迹
,
不写作法
)
.
(2)
如图
25-17
②
,
直线
l
与☉
O
相切于点
P
,
且
l
∥
BC.
图
25-17
|
考向精练
|
1
.
[2019·
江西
15
题
]
在
△
ABC
中
,
AB=AC
,
点
A
在以
BC
为直径的半圆内
,
请仅用无刻度的直尺分别按下列要求画图
(
保留画图痕迹
)
.
(1)
在图
25-18
①中作弦
EF
,
使
EF
∥
BC
;
(2)
在图
25-18
②中以
BC
为边作一个
45°
的圆周角
.
图
25-18
解
:(1)
如图①
,
EF
即为所求
.
1
.
[2019·
江西
15
题
]
在
△
ABC
中
,
AB=AC
,
点
A
在以
BC
为直径的半圆内
,
请仅用无刻度的直尺分别按下列要求画图
(
保留画图痕迹
)
.
(2)
在图
25-18
②中以
BC
为边作一个
45°
的圆周角
.
图
25-18
(2)
如图②
,
∠
MBC
即为所求
.
2
.
[2018·
芦溪模拟
]
如图
25-19,
AB
是☉
O
的直径
,
AC
是☉
O
的切线
,
AC=AB
,
请仅用无刻度的直尺画图
(
保留作图痕迹
,
不写作法
)
.
(1)△
ABC
的中线
BE
;
(2)
以
D
为切点作☉
O
的切线
DT.
图
25-19
解
:(1)
如图①
,
BE
即为所求
;
(2)
如图②
,
DT
即为所求
.
3
.
[2019·
抚州模拟
]
如图
25-20,
线段
AB
是☉
O
的直径
,
BC
⊥
CD
于点
C
,
AD
⊥
CD
于点
D
,
请仅用无刻度的直尺按下列要求作图
.
(1)
在图
25-20
①中
,
当线段
CD
与☉
O
相切时
,
请在
CD
上确定一点
E
,
连接
BE
,
使
BE
平分∠
ABC
;
(2)
在图
25-20
②中
,
当线段
CD
与☉
O
相离时
,
请过点
O
作
OF
⊥
CD
,
垂足为
F.
图
25-20
解
:(1)
如图①
,
BE
即为所求
.
3
.
[2019·
抚州模拟
]
如图
25-20,
线段
AB
是☉
O
的直径
,
BC
⊥
CD
于点
C
,
AD
⊥
CD
于点
D
,
请仅用无刻度的直尺按下列要求作图
.
(2)
在图
25-20
②中
,
当线段
CD
与☉
O
相离时
,
请过点
O
作
OF
⊥
CD
,
垂足为
F.
图
25-20
(2)
如图②
,
OF
即为所求
.